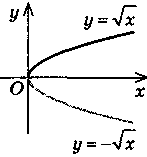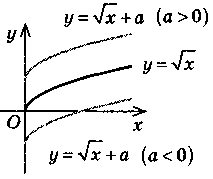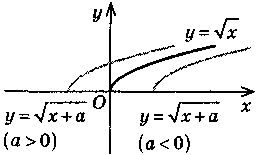- •1. Дійсні числа. Дії над дійсними числами
- •2. Об’єм кулі та її частин
- •1. Радіанне вимірювання кутів. Тригонометричні функції числового аргументу.
- •2. Об’єм циліндра і конуса
- •1. Комплексні числа. Дії над комплексними числами в алгебраїчній формі.
- •2. Поняття об’єму тіла. Об’єм призми, піраміди
- •1. Комплексні числа. Тригонометрична форма комплексного числа.
- •2. Взаємне розташування прямих. Ознака мимобіжності прямих.
- •Доведення
- •1. Квадратні рівняння з від’ємним дискримінантом
- •2. Конус. Осьовий переріз конуса. Переріз конуса площинами
- •1. Числова функція. Область визначення та множина значень
- •2. Піраміда. Види піраміди. Переріз піраміди площиною паралельною основі
- •1. Монотонність, обмеженість, парність, непарність, періодичність функцій
- •2. Многогранники. Паралелепіпед та його властивості.
- •1. Найпростіші перетворення графіків функцій
- •2. Поняття про статистику. Мода, медіана, середні значення.
- •1. Числові послідовності та їх класифікація
- •Способи задання числових послідовностей:
- •2. Перпендикулярність площин. Ознака перпендикулярності площин.
- •Доведення
- •1. Границя функції в точці. Основні властивості границь.
- •2. Циліндр. Осьовий переріз циліндра. Переріз циліндра площинами
- •2. Призма. Правильна призма. Площа бічної поверхні прямої призми.
- •2. Прямокутний паралелепіпед. Центральна симетрія паралелепіпеда.
- •1. Залежність між тригонометричними функціями одного і того самого аргументу.
- •2. Циліндр. Формули об’єму циліндра та площі повної поверхні циліндра
- •1. Тригонометричні функції подвійного аргументу
- •2. Декартові координати у просторі. Відстань між точками у просторі
- •Доведення
- •2. Правильна піраміда, Площа бічної поверхні правильної піраміди.
- •2. Конус. Формули об’єму конуса та площі повної поверхні конуса.
- •1. Корінь п –го степеня і його властивості.
- •2. Взаємне розміщення прямої і площини в просторі. Ознака паралельності прямої і площини
- •Доведення
- •1. Степенева функція з цілим показником, її графік і властивості
- •2. Взаємне розміщення двох площин у просторі. Ознака паралельності двох площин.
- •Доведення
- •1. Показникова функція, її графік і властивості.
- •2. Вектори у просторі. Дії над векторами. Множення вектора на число, його властивості.
- •1. Логарифм числа. Логарифм частки.
- •2. Перпендикулярність площин. Ознака перпендикулярності площин
- •Доведення
- •2. Куля. Переріз кулі площиною. Формули об’єму кулі та площі сфери.
- •1. Похідна функції. Похідна суми, добутку та частки двох функцій.
- •2. Перпендикулярність прямої і площини. Ознака перпендикулярності прямої і площини.
- •1. Похідна функції. Похідні показникової, логарифмічної та тригонометричних функцій.
- •2. Перпендикуляр і похила до площини. Теорема про три перпендикуляри.
- •1. Геометричний зміст похідної. Рівняння дотичної до графіка функції.
- •2. Паралелепіпед та його властивості.
- •Властивості :
- •1. Первісна. Основна властивість первісної.
- •Доведення
- •Доведення
- •2. Пряма і правильна призми. Площі бічної та повної поверхні призми.
- •1. Первісна. Правила знаходження первісних.
- •2. Циліндр. Осьовий переріз циліндра. Формули об’єму та повної поверхні циліндра
- •1. Загальна схема дослідження функції за допомогою похідної
- •2. Ознака колінеарності векторів
- •1. Визначений інтеграл, його геометричний зміст та властивості
- •2. Паралельне проектування та його властивості. Ортогональне проектування.
- •Відрізки зображаються відрізками;
- •Паралельні відрізки зображаються паралельними відрізками або відрізками однієї прямої;
- •3) Відношення довжин паралельних відрізків і відрізків однієї прямої зберігається.
- •1. Екстремуми функції. Дослідження функцій на екстремум.
- •2. Основні поняття теорії ймовірностей. Класичне означення ймовірностей
1. Монотонність, обмеженість, парність, непарність, періодичність функцій
Ф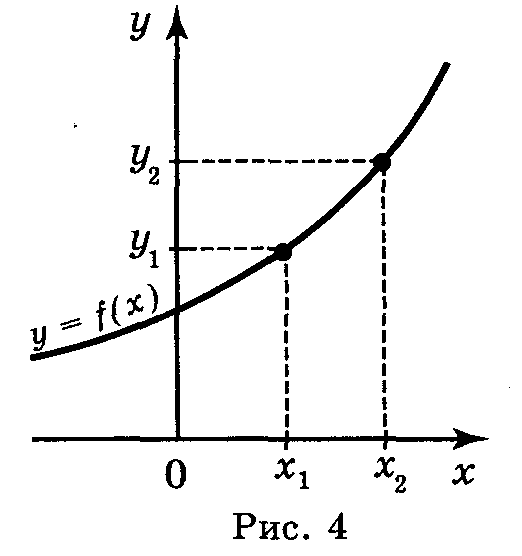 ункція
у
= f(x)
називається зростаючою
(рис. 4), якщо більшому значенню аргументу
відповідає більше значення функції,
тобто для будь-яких значень х1
і х2
з
області визначення функції таких, що
х1
< х2,
виконується нерівність f(x1)
< f(x2)
і навпаки: із того, що f(x1)
< f(x2)
виконується нерівність х1
< х2.
ункція
у
= f(x)
називається зростаючою
(рис. 4), якщо більшому значенню аргументу
відповідає більше значення функції,
тобто для будь-яких значень х1
і х2
з
області визначення функції таких, що
х1
< х2,
виконується нерівність f(x1)
< f(x2)
і навпаки: із того, що f(x1)
< f(x2)
виконується нерівність х1
< х2.
Ф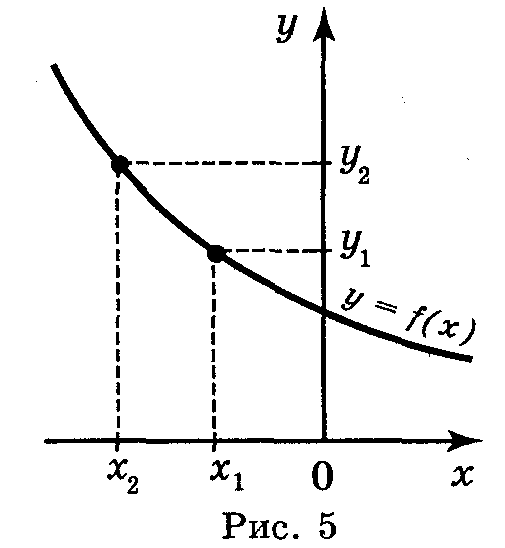 ункція
у
=
f(x)
називається спадною
(рис.
5), якщо більшому значенню аргументу
відповідає менше значення функції,
тобто для будь-яких значень х1
і
х2
з
області визначення функції таких,
що х1
< х2,
виконується нерівність f(x1)
> f(x2)
і навпаки: якщо у
= f(x)
—
спадна, то із того, що f(x1)
> f(x2),
виконується нерівність х1
< х2.
ункція
у
=
f(x)
називається спадною
(рис.
5), якщо більшому значенню аргументу
відповідає менше значення функції,
тобто для будь-яких значень х1
і
х2
з
області визначення функції таких,
що х1
< х2,
виконується нерівність f(x1)
> f(x2)
і навпаки: якщо у
= f(x)
—
спадна, то із того, що f(x1)
> f(x2),
виконується нерівність х1
< х2.
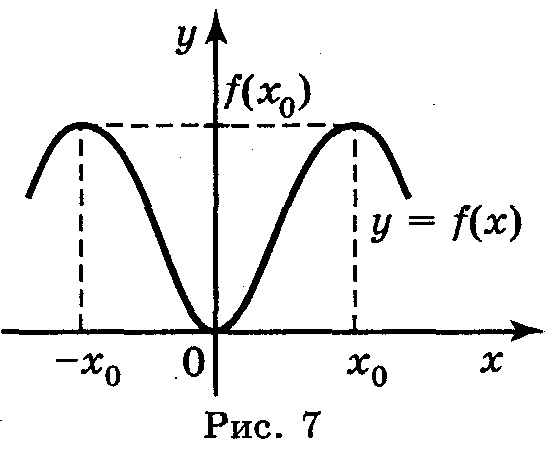
Функція у = f(x) називається парною, якщо для будь-якого значення х із D(y) значення – х також належить D(y) і виконується рівність f(-x) = f(x).
Графік парної функції симетричний відносно осі ОУ (рис. 7).
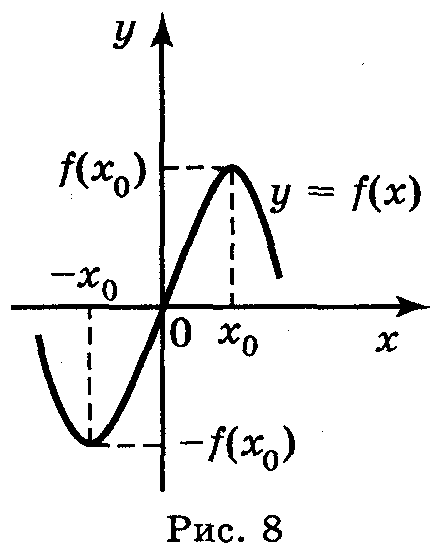
Функція у = f(x) називається непарною, якщо для будь-якого значення х із D(y) значення -х є D(y) і виконується рівність f(-x) = -f(х).
Графік непарної функції симетричний відносно початку координат (рис. 8).
Функція у = f(x) називається періодичною з періодом Т 0, якщо для будь-якого х із області визначення числа х + Т і х – Т також належать області визначення і виконується рівність f(x + Т) = f(x – Т) = f(x).
Приклад, період тангенса і котангенса дорівнює π, а період косинуса і синуса дорівнює 2π.
2. Многогранники. Паралелепіпед та його властивості.
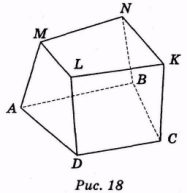
Многогранником називають тіло (частина простору), обмежене скінченою
кількістю плоских многокутників (рис. 18).
Многокутники, які обмежують многогранник, називають його гранями, їх сторони
— ребрами, а вершини — вершинами многогранника.
Многогранник називається опуклим, якщо він лежить по один бік від площини кожного з плоских многокутників на його поверхні.
 Прикладами
опуклих многогранників можуть бути
куб, прямокутний паралелепіпед,
тетраедр тощо.
Прикладами
опуклих многогранників можуть бути
куб, прямокутний паралелепіпед,
тетраедр тощо.
Паралелепіпедом називається призма в основі якої лежить паралелограм.
♦ Протилежні грані паралелепіпеда паралельні та рівні.
♦ Діагоналі паралелепіпеда перетинаються в одній точці і точкою перетину діляться пополам
♦ Точка перетину паралелепіпеда є його центром симетрії.
♦ Паралелепіпед в основі якого лежить прямокутник називається прямим.
♦ У прямокутному паралелепіпеді квадрат будь-якої діагоналі дорівнює сумі квадратів трьох
його вимірів
Білет № 8
Найпростіші перетворення графіків функцій.
Поняття про статистику. Мода, медіана, середні значення.
Обчислити:
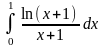
В циліндрі площа основи дорівнює Q, а площа осьового перерізу S. Визначити повну поверхню циліндра.
1. Найпростіші перетворення графіків функцій
№ з/п |
Формула залежності |
Приклад |
Перетворення |
1 |
y = -f(х) |
|
Симетрія відносно осі Ох |
2 |
y = f(х) + a |
|
Паралельне перенесення вздовж осі Оу на а одиниць (якщо а > 0, то вгору, якщо а < 0, то вниз) |
3 |
y = f(х + a) |
|
Паралельне перенесення вздовж осі Ох на +а одиниць (якщо а > 0 — вліво, якщо а < 0 — вправо) |
4 |
y = kf(х) (k > 0) |
|
Той самий вигляд, що і y = f(x), тільки розтяг-нуто, якщо k > 1, і стиснуто, якщо 0 < k < 1 |