1. Числова функція. Область визначення та множина значень

Числовою функцією з областю визначення D називається за­лежність, при якій кожному числу х із множини D ставиться у відповідність по деякому правилу єдине число у із множини Е.

Змінна х називається незалежною змінною або аргументом функції, а змінна у — залежною змінною або функцією.

Область визначення функції позначається D(f). Множина, яка складається із всіх чисел f(x) таких, що х належить області визначення функції f, називаєть­ся областю значень функції і позначається E(f).

Областю визначення функції у = f(x), яка задана формулою, називається множина тих значень, які може приймати х, тобто формула має зміст (усі дії, вказані формулою, можна виконати). При знаходженні області визначення слід пам'ятати:

1. Якщо функція є многочленом у = а_n хⁿ + α_n-1 x^n-1 +... + α₁x + a₀,

то D(y) = (-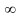 ; + ) = R.

2) Якщо функція має вигляд у = 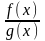, де f(x) і g(x) — многочлени, то слід вважати g(x )≠ 0 (знаменник дробу не дорів­нює 0).

3) Якщо функція має вигляд у = 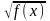, то слід вважати f(x) > 0 (арифметичний квадратний корінь існує тільки з невід'ємних чисел).

2. Піраміда. Види піраміди. Переріз піраміди площиною паралельною основі

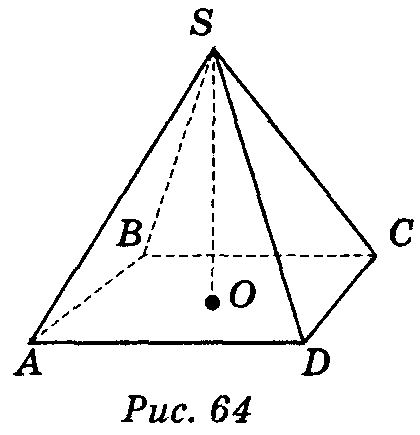n-кутною пірамідою називається многогранник, одна грань яко­го — довільний n-кутний, всі інші n граней — трикутники, що ма­ють спільну вершину.

Спільну вершину трикутних граней на­зивають вершиною піраміди, протилежну їй грань — основою, а всі інші грані — бічни­ми гранями піраміди.

Відрізки, що сполучають вершину піра­міди з вершинами основи, називають бічни­ми ребрами.

Перпендикуляр, опущений з вершини пі­раміди на площину її основи, називають ви­сотою піраміди. Висотою також називають і довжину цього перпендикуляра.

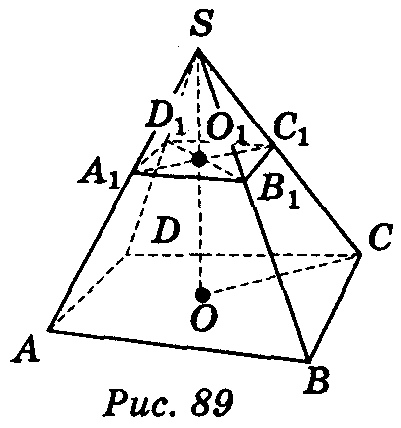
Площина, паралельна основі піраміди, розтинає її на піраміду і фігуру, яка називається зрізаною пірамідою. Піраміда, що відтинається цією площиною, подібна даній.

Грані зрізаної піраміди, що лежать у паралельних площинах, називаються основами піраміди; всі інші грані – бічні грані піраміди. Основи зрізаної піраміди – гомотетичні многокутники. Кожна з бічних граней зрізаної піраміди – трапеція.

Площина, паралельна основі піраміди, розтинає її на піраміду і фігуру, яка називається зрізаною пірамідою. Піраміда, що відтинається цією площиною, подібна даній.

Грані зрізаної піраміди, що лежать у паралельних площинах, називаються основами піраміди; всі інші грані – бічні грані піраміди. Основи зрізаної піраміди – гомотетичні многокутники. Кожна з бічних граней зрізаної піраміди – трапеція.

Білет № 7

1. Монотонність, обмеженість, парність, непарність, періодичність функцій.

2. Многогранники. Призма. Паралелепіпед та його властивості.

3. Запишіть у вигляді степеня .

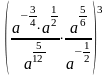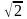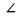4. Через вершину прямого кута В трикутника АВС до площини проведено перпендикуляр ВК, довжина якого дорівнює 7 см. Знайдіть відстань від точки К до прямої АС, якщо АС = 8 см, ВАС = 45⁰.