1. Комплексні числа. Тригонометрична форма комплексного числа.

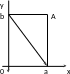
Крім алгебраїчної форми запису комплексного числа застосовують також іншу, яка називається тригонометричною. Нехай комплексне число 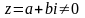зображується вектором 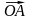з координатами (а;b). Позначимо довжину вектора буквою r:

,

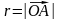а кут, який він утворює з додатним напрямом осі Ох, - через 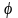(кут вважається виміряним у радіанах) (рис.81).

Скориставшись означеннями функцій і :

, ,

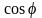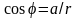комплексне число z = а + bі можна записати у вигляді

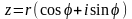, (1)

де 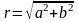, а кут φ позначається з умов , 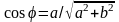. (2)

Вираз (1) має назву тригонометрична форма запису комплексного числа. Дійсне число r є модулем комплексного числа і позначається |z|, а кут , виміряний в радіанах, - його аргументом і позначається Argz.

2. Взаємне розташування прямих. Ознака мимобіжності прямих.

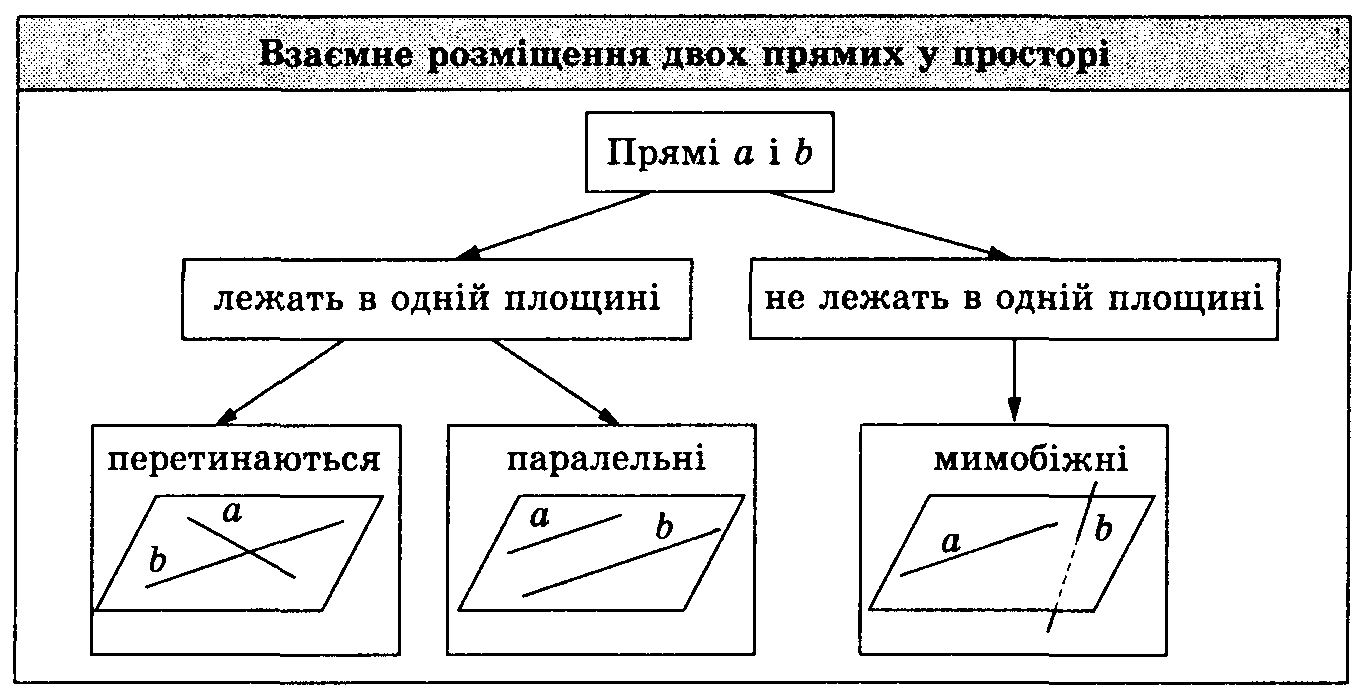
Прямі, які не перетинаються і лежать в одній площині, називають паралельними, а дві прямі, які не перетинаються і не лежать в одній площині, називають мимобіжними.

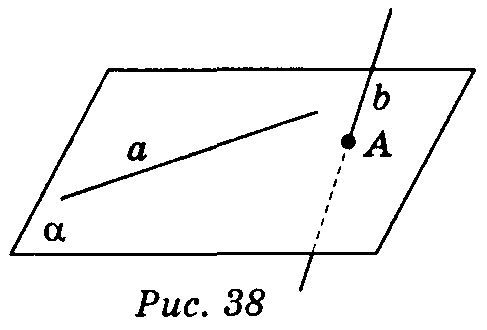
Теорема (ознака мимобіжності прямих)

Якщо одна з двох прямих лежить у площині, а друга пере­тинає цю площину в точці, яка не лежить на першій пря­мій, то ці прямі мимобіжні.

Доведення

Нехай пряма а лежить у площині α , а пряма b перетинає цю площину в точці А такій, що А α (рис. 38). Доведемо, що прямі а і b мимобіжні. Припустимо, що прямі a і b не мимобіжні, тобто вони лежать в деякій площині β . Площина β проходить через пряму а і точку А і тому збігається з площиною α . Таким чином, пряма b лежить в площині α, що супере­чить умові. Отже, прямі a і b не лежать в одній площині, що і треба було довести.

Білет № 5

1. Квадратні рівняння з від’ємним дискримінантом.

2. Конус. Осьовий переріз конуса. Переріз конуса площинами

3. Обчислити: .

4. Основою прямого паралелепіпеда є ромб зі стороною а і гострим кутом . Менша діагональ паралелепіпеда нахилена до площини основи під кутом 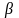. Знайдіть площу бічної поверхні паралелепіпеда.

1. Квадратні рівняння з від’ємним дискримінантом

Квадратне рівняння — це рівняння виду ax² + bx + c = 0, де a не дорівнює 0.

Для розв'язання квадратного рівняння необхідно порахувати дискримінант

D = b²- 4ac.

Якщо D > 0, то рівняння має два різних дійсних кореня: х_1,2=

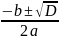
Якщо D = 0, то обидва кореня дійсні і рівні: х_1,2=

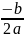
Якщо D < 0, то оба кореня комплексні числа: х_1,2=

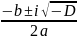
2. Конус. Осьовий переріз конуса. Переріз конуса площинами

Прямим круговим конусом називається тіло, утворене обертанням плоского прямокутного трикутника навколо одного із його катетів .

Радіус цього круга називається радіусом конуса; то­чка S, відрізок SА, відрізок SO, пряма SO називаються відповідно вершиною, твірною, висотою і віссю конуса.

Осьовий переріз конуса — переріз конуса площиною, яка проходить через його вісь. Всі осьові перерізи конуса являють собою рівнобедрені трикутники, рівні між собою.

На рис. 125 ∆SАВ — осьовий переріз (SА = SВ).

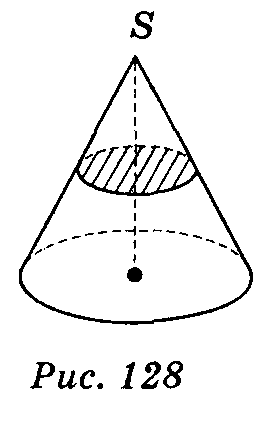Висотою конуса називається перпендикуляр, опущений з його вершини на площину основи. У прямого кругового конуса основа висоти збігається з центром основи.

Площина, паралельна площині основи конуса, перетинає конус по кругу, а бічну поверхню — по колу з центром на осі конуса.

Білет № 6

1. Числова функція. Область визначення та множина значень.

2. Піраміда. Види піраміди. Переріз піраміди площиною паралельною основі.

3. Знайти площу фігури, обмеженої лініями у = sin x, y = 0, x = 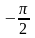, x = .

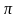4. Через гіпотенузу прямокутного рівнобедреного трикутника проведено площину, яка утворює з площиною трикутника кут 45⁰. Знайдіть кути, які утворюють катети трикутника з цією площиною.