
- •1. Дійсні числа. Дії над дійсними числами
- •2. Об’єм кулі та її частин
- •1. Радіанне вимірювання кутів. Тригонометричні функції числового аргументу.
- •2. Об’єм циліндра і конуса
- •1. Комплексні числа. Дії над комплексними числами в алгебраїчній формі.
- •2. Поняття об’єму тіла. Об’єм призми, піраміди
- •1. Комплексні числа. Тригонометрична форма комплексного числа.
- •2. Взаємне розташування прямих. Ознака мимобіжності прямих.
- •Доведення
- •1. Квадратні рівняння з від’ємним дискримінантом
- •2. Конус. Осьовий переріз конуса. Переріз конуса площинами
- •1. Числова функція. Область визначення та множина значень
- •2. Піраміда. Види піраміди. Переріз піраміди площиною паралельною основі
- •1. Монотонність, обмеженість, парність, непарність, періодичність функцій
- •2. Многогранники. Паралелепіпед та його властивості.
- •1. Найпростіші перетворення графіків функцій
- •2. Поняття про статистику. Мода, медіана, середні значення.
- •1. Числові послідовності та їх класифікація
- •Способи задання числових послідовностей:
- •2. Перпендикулярність площин. Ознака перпендикулярності площин.
- •Доведення
- •1. Границя функції в точці. Основні властивості границь.
- •2. Циліндр. Осьовий переріз циліндра. Переріз циліндра площинами
- •2. Призма. Правильна призма. Площа бічної поверхні прямої призми.
- •2. Прямокутний паралелепіпед. Центральна симетрія паралелепіпеда.
- •1. Залежність між тригонометричними функціями одного і того самого аргументу.
- •2. Циліндр. Формули об’єму циліндра та площі повної поверхні циліндра
- •1. Тригонометричні функції подвійного аргументу
- •2. Декартові координати у просторі. Відстань між точками у просторі
- •Доведення
- •2. Правильна піраміда, Площа бічної поверхні правильної піраміди.
- •2. Конус. Формули об’єму конуса та площі повної поверхні конуса.
- •1. Корінь п –го степеня і його властивості.
- •2. Взаємне розміщення прямої і площини в просторі. Ознака паралельності прямої і площини
- •Доведення
- •1. Степенева функція з цілим показником, її графік і властивості
- •2. Взаємне розміщення двох площин у просторі. Ознака паралельності двох площин.
- •Доведення
- •1. Показникова функція, її графік і властивості.
- •2. Вектори у просторі. Дії над векторами. Множення вектора на число, його властивості.
- •1. Логарифм числа. Логарифм частки.
- •2. Перпендикулярність площин. Ознака перпендикулярності площин
- •Доведення
- •2. Куля. Переріз кулі площиною. Формули об’єму кулі та площі сфери.
- •1. Похідна функції. Похідна суми, добутку та частки двох функцій.
- •2. Перпендикулярність прямої і площини. Ознака перпендикулярності прямої і площини.
- •1. Похідна функції. Похідні показникової, логарифмічної та тригонометричних функцій.
- •2. Перпендикуляр і похила до площини. Теорема про три перпендикуляри.
- •1. Геометричний зміст похідної. Рівняння дотичної до графіка функції.
- •2. Паралелепіпед та його властивості.
- •Властивості :
- •1. Первісна. Основна властивість первісної.
- •Доведення
- •Доведення
- •2. Пряма і правильна призми. Площі бічної та повної поверхні призми.
- •1. Первісна. Правила знаходження первісних.
- •2. Циліндр. Осьовий переріз циліндра. Формули об’єму та повної поверхні циліндра
- •1. Загальна схема дослідження функції за допомогою похідної
- •2. Ознака колінеарності векторів
- •1. Визначений інтеграл, його геометричний зміст та властивості
- •2. Паралельне проектування та його властивості. Ортогональне проектування.
- •Відрізки зображаються відрізками;
- •Паралельні відрізки зображаються паралельними відрізками або відрізками однієї прямої;
- •3) Відношення довжин паралельних відрізків і відрізків однієї прямої зберігається.
- •1. Екстремуми функції. Дослідження функцій на екстремум.
- •2. Основні поняття теорії ймовірностей. Класичне означення ймовірностей
1. Загальна схема дослідження функції за допомогою похідної
Дослідження функції і побудову її графіка будемо виконувати за таким планом:
1. Знаходимо область визначення функції.
2. Знаходимо точки перетину графіка з координатними осями.
3. З'ясовуємо парність (непарність), періодичність функції.
4. Знаходимо похідну та стаціонарні точки.
5. Знаходимо проміжки зростання, спадання, точки екстремуму та екстремальні значення функції.
6. З'ясовуємо поведінку функції на кінцях області визначення.
7. На підставі проведеного дослідження будуємо графік функції
2. Ознака колінеарності векторів
Вектором називають напрямлений відрізок.
Вектор, у якого початок збігається з кінцем, називається нульовим вектором. Ненульові вектори називаються колінеарними, якщо вони лежать або на одній прямій, або на паралельних прямих. Ненульові вектори і називаються однаково напрямленими, якщо вони колінеарні та напрямлені в один бік.
Ознака колінеарності векторів
Якщо вектори колінеарні, то їхні відповідні координати пропорційні. І навпаки, якщо відповідні координати двох векторів пропорційні, то ці вектори колінеарні.


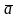 ll
ll
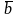
Білет № 29
Визначений інтеграл, його геометричний зміст та властивості.
Паралельне проектування та його властивості. Ортогональне проектування.
Обчисліть площу фігури, обмеженої лініями: у =
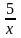 , у = 4х + 1, х = 2.
, у = 4х + 1, х = 2.У правильній трикутній призмі АВСА1В1С1 сторона основи дорівнює 8 см, а бічне ребро – 2 см. Через сторону АС нижньої основи і середину сторони А1В1 верхньої проведено площину. Знайдіть площу перерізу.
1. Визначений інтеграл, його геометричний зміст та властивості
Визначений інтеграл записується у вигляді формули Ньютона-Лейбніца
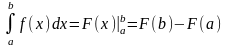
де
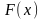 -
первісна функції
-
первісна функції
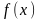 або невизначений інтеграл.
або невизначений інтеграл.
Властивості визначеного інтеграла:
Визначений інтеграл має ті ж властивості, що й невизначений. Крім того:
1о. Якщо відрізок інтегрування [a, b] розбитий на дві частини [a, с] і [с, b], то
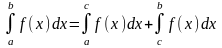 .
.
2о.
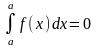 .
.
3о.
 ,
якщо
,
якщо
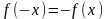 .
.
4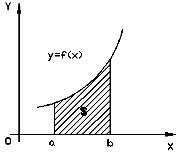 о.
о.
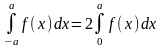 ,
якщо
,
якщо
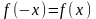 .
.
Геометричний зміст визначеного інтеграла:
![]() де
S-
площа фігури, обмеженої графіком функції
y = f(x) і прямими х
= а, х = b і y = 0.
де
S-
площа фігури, обмеженої графіком функції
y = f(x) і прямими х
= а, х = b і y = 0.
Криволінійною трапецією називається фігура, обмежена графіком неперервної функції у = f(x), яка не змінює знак на відрізку [а; b], прямими x = а, х = b і відрізком [а; b]
