2. Об’єм циліндра і конуса

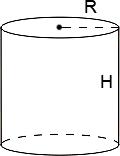
Об'єм циліндра дорівнює добутку площі його основи на висоту:

О б’єм конуса дорівнює третині добутку площі його основи на висоту:

Білет № 3

1. Комплексні числа. Дії над комплексними числами в алгебраїчній формі.

2. Поняття об’єму тіла. Об’єм призми, піраміди.

3. Дослідити функцію на монотонність на екстремуми і побудувати її графік f(x) = .

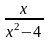4. В основі прямої призми лежить рівнобічна трапеція з бічною стороною с і гострим кутом α. Діагоналі цієї трапеції взаємно перпендикулярні. Діагональ призми утворює з площиною основи кут γ. Визначити об’єм призми.

1. Комплексні числа. Дії над комплексними числами в алгебраїчній формі.

Число , де і – будь-які дійсні числа, – уявна одиниця, називається комплексним числом ( – дійсна частина, – уявна частина комплексного числа, а – коефіцієнт при уявній частині).

Число, квадрат якого дорівнює –1, позначають буквою і і називають уявною одиницею ( – перша буква латинського слова imaginarius – уявний).

Тобто, для символу виконується рівність

.

Запис називають алгебраїчною формою комплексного числа.

Тому дії над комплексними числами а + bі виконуються так, як і дії над многочленами, вважаючи, що і² = -1.

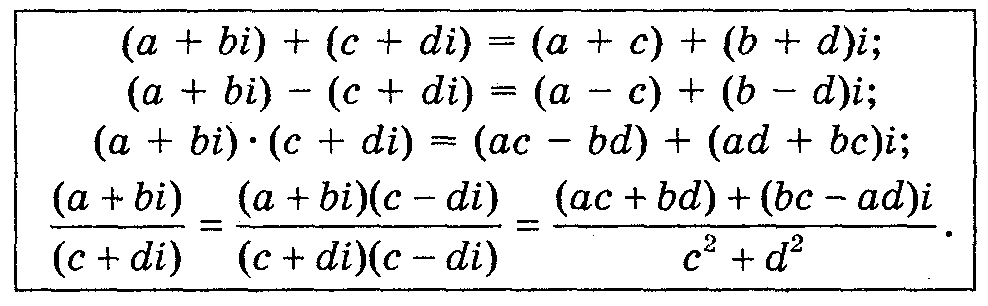
Виконайте дії:

1) (3 – 5i) + (2 + і) = 3 – 5i + 2 + i = (3 + 2) + (-5і + i)= 5 – 4i;

2) (3 - 5і) - (2 + i) = 3 – 5i - 2 - і = (3 - 2) + (-5і - i) = 1 – 6i;

3) (4 + 7і)(2 – i) = 8 + 14i – 4i – 7i² = 8 + 14i – 4i + 7 = - (8+7)+(14i–4i)–15+ 10i;

2. Поняття об’єму тіла. Об’єм призми, піраміди

Об'ємом геометричного тіла будемо називати додатне число, яке характеризує частину простору, що займає геометричне тіло, і за­довольняє таким умовам:

1. Рівні тіла мають рівні об'єми.

2. Якщо тіло розбите на кілька частин, то його об'єм дорівнює сумі об'ємів усіх цих частин.

3. Об'єм куба, ребро якого дорівнює одиниці довжини, дорівнює одиниці.

Куб, довжина ребра якого дорівнює одиниці довжини, називають одиничним.

Об'єм одиничного куба приймають за одиницю об'єму, називаючи таку одиницю кубічною.

Наприклад: кубічний сантиметр — це об'єм куба, ребро якого дорів­нює 1 см

Об’єм будь-якої призми дорівнює добутку площі основи та висоти.

V_пр = S _осн ∙ Н. На рисунках наведені приклади призм із різними основами. Для прямокутного паралелепіпеда отримаємо V = a ∙ b ∙ c , де a, b, c — його виміри. Для куба V = a³ , де a — довжина ребра. Для похилої призми (рисунок нижче зліва) об’єм можна обчислити як добуток площі перпендикулярного перерізу та довжини бічного ребра: V = Q ∙ l Об’єм будь-якої піраміди (рисунок справа) дорівнює третині добутку площі її основи та висоти: V_пір = 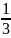S _осн ∙Н. Об’єм зрізаної піраміди (див. рисунок) дорівнює:

,

де H — висота, S ₁ - площа нижньої основи, S ₂ - площа верхньої основи.

Білет № 4

1. Комплексні числа. Тригонометрична форма комплексного числа.

2. Взаємне розташування прямих. Ознака мимобіжності прямих.

3. Обчислити: .

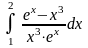4. Знайти центральні тенденції вибірки: 12, 17, 11, 13, 14, 15, 15, 16, 13, 13.