
- •1. Дійсні числа. Дії над дійсними числами
- •2. Об’єм кулі та її частин
- •1. Радіанне вимірювання кутів. Тригонометричні функції числового аргументу.
- •2. Об’єм циліндра і конуса
- •1. Комплексні числа. Дії над комплексними числами в алгебраїчній формі.
- •2. Поняття об’єму тіла. Об’єм призми, піраміди
- •1. Комплексні числа. Тригонометрична форма комплексного числа.
- •2. Взаємне розташування прямих. Ознака мимобіжності прямих.
- •Доведення
- •1. Квадратні рівняння з від’ємним дискримінантом
- •2. Конус. Осьовий переріз конуса. Переріз конуса площинами
- •1. Числова функція. Область визначення та множина значень
- •2. Піраміда. Види піраміди. Переріз піраміди площиною паралельною основі
- •1. Монотонність, обмеженість, парність, непарність, періодичність функцій
- •2. Многогранники. Паралелепіпед та його властивості.
- •1. Найпростіші перетворення графіків функцій
- •2. Поняття про статистику. Мода, медіана, середні значення.
- •1. Числові послідовності та їх класифікація
- •Способи задання числових послідовностей:
- •2. Перпендикулярність площин. Ознака перпендикулярності площин.
- •Доведення
- •1. Границя функції в точці. Основні властивості границь.
- •2. Циліндр. Осьовий переріз циліндра. Переріз циліндра площинами
- •2. Призма. Правильна призма. Площа бічної поверхні прямої призми.
- •2. Прямокутний паралелепіпед. Центральна симетрія паралелепіпеда.
- •1. Залежність між тригонометричними функціями одного і того самого аргументу.
- •2. Циліндр. Формули об’єму циліндра та площі повної поверхні циліндра
- •1. Тригонометричні функції подвійного аргументу
- •2. Декартові координати у просторі. Відстань між точками у просторі
- •Доведення
- •2. Правильна піраміда, Площа бічної поверхні правильної піраміди.
- •2. Конус. Формули об’єму конуса та площі повної поверхні конуса.
- •1. Корінь п –го степеня і його властивості.
- •2. Взаємне розміщення прямої і площини в просторі. Ознака паралельності прямої і площини
- •Доведення
- •1. Степенева функція з цілим показником, її графік і властивості
- •2. Взаємне розміщення двох площин у просторі. Ознака паралельності двох площин.
- •Доведення
- •1. Показникова функція, її графік і властивості.
- •2. Вектори у просторі. Дії над векторами. Множення вектора на число, його властивості.
- •1. Логарифм числа. Логарифм частки.
- •2. Перпендикулярність площин. Ознака перпендикулярності площин
- •Доведення
- •2. Куля. Переріз кулі площиною. Формули об’єму кулі та площі сфери.
- •1. Похідна функції. Похідна суми, добутку та частки двох функцій.
- •2. Перпендикулярність прямої і площини. Ознака перпендикулярності прямої і площини.
- •1. Похідна функції. Похідні показникової, логарифмічної та тригонометричних функцій.
- •2. Перпендикуляр і похила до площини. Теорема про три перпендикуляри.
- •1. Геометричний зміст похідної. Рівняння дотичної до графіка функції.
- •2. Паралелепіпед та його властивості.
- •Властивості :
- •1. Первісна. Основна властивість первісної.
- •Доведення
- •Доведення
- •2. Пряма і правильна призми. Площі бічної та повної поверхні призми.
- •1. Первісна. Правила знаходження первісних.
- •2. Циліндр. Осьовий переріз циліндра. Формули об’єму та повної поверхні циліндра
- •1. Загальна схема дослідження функції за допомогою похідної
- •2. Ознака колінеарності векторів
- •1. Визначений інтеграл, його геометричний зміст та властивості
- •2. Паралельне проектування та його властивості. Ортогональне проектування.
- •Відрізки зображаються відрізками;
- •Паралельні відрізки зображаються паралельними відрізками або відрізками однієї прямої;
- •3) Відношення довжин паралельних відрізків і відрізків однієї прямої зберігається.
- •1. Екстремуми функції. Дослідження функцій на екстремум.
- •2. Основні поняття теорії ймовірностей. Класичне означення ймовірностей
2. Паралелепіпед та його властивості.
Паралелепіпедом називається призма в основі якої лежить паралелограм.
Розрізняється декілька типів паралелепіпедів:
Прямокутний паралелепіпед - це паралелепіпед, у якого всі грані прямокутники;
Прямий паралелепіпед - це паралелепіпед, у якого 4 бічні грані прямокутники;
Похилий паралелепіпед - це паралелепіпед, бічні грані якого не перпендикулярні підставах.
Куб - це прямокутний паралелепіпед з рівними вимірами. Всі шість граней куба - рівні квадрати.
Властивості :
♦ Протилежні грані паралелепіпеда паралельні та рівні.
♦ Діагоналі паралелепіпеда перетинаються в одній точці і точкою перетину діляться пополам
♦ Точка перетину паралелепіпеда є його центром симетрії.
♦ Паралелепіпед в основі якого лежить прямокутник називається прямим.
♦ У прямокутному паралелепіпеді квадрат будь-якої діагоналі дорівнює сумі квадратів трьох його вимірів
Білет № 26
Первісна. Основна властивість первісної.
Пряма і правильна призми. Площі бічної та повної поверхні призми.
Розв’яжіть рівняння: 27
 +
2 3
+
2 3
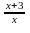 –
27 = 0.
–
27 = 0.Через вершину прямого кута С трикутника АВС до площини трикутника проведено перпендикуляр КС, довжина якого дорівнює 4
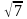 см. Знайдіть відстань від точки К до
прямої АВ, якщо АС = ВС = 8 см.
см. Знайдіть відстань від точки К до
прямої АВ, якщо АС = ВС = 8 см.
1. Первісна. Основна властивість первісної.
Функція F(x) називається первісною функції f(x) на деякому проміжку, якщо для всіх x із цього проміжку виконується рівність: F'(X) = f(x).
Теореми 1 і 2 виражають основну властивість первісної
Теорема 1. Нехай функція F(x) є первісною для f(х) на деякому проміжку. Тоді для довільної постійної С функція F(x) + С також є первісною для функції f(х).
Доведення
Оскільки F(x) — первісна функції f(x), то F'(x) = f(x). Тоді (F(x) + С)' = F'(x) + С' = f(х) + 0 = f(x), а ця рівність означає, що F(x) + С є первісною для функції f(х).
Теорема 2. Нехай функція F(x) є первісною для f(x) на деякому проміжку. Тоді будь-яка первісна для функції f(x) на цьому проміжку може бути записана у вигляді F(x) + С, де С — деяка стала (число).
Доведення
Н ехай
F(x)
і F1(x)
—
дві первісні однієї і тієї самої функції
f(x),
тобто F'(x
)
= f(x),
F1'(x
) = f(x).
Похідна різниці g(x)
= F(x)
– F1(x)
дорівнює нулю, оскільки g'(x)
= F1'(x
) - F'(x)
= = f(x)
- f(x)
= 0. Якщо
g'(x)
= 0 на деякому проміжку, то дотична до
графіка функції у
=
g(x)
у кожній точці цього проміжку паралельна
осі ОХ.
Тому графіком функції у
=
g(x)
є пряма, яка паралельна осі ОХ,
тобто
g(x)
= С, де С
—
деяка стала. Із рівностей
g(x)
= С,
ехай
F(x)
і F1(x)
—
дві первісні однієї і тієї самої функції
f(x),
тобто F'(x
)
= f(x),
F1'(x
) = f(x).
Похідна різниці g(x)
= F(x)
– F1(x)
дорівнює нулю, оскільки g'(x)
= F1'(x
) - F'(x)
= = f(x)
- f(x)
= 0. Якщо
g'(x)
= 0 на деякому проміжку, то дотична до
графіка функції у
=
g(x)
у кожній точці цього проміжку паралельна
осі ОХ.
Тому графіком функції у
=
g(x)
є пряма, яка паралельна осі ОХ,
тобто
g(x)
= С, де С
—
деяка стала. Із рівностей
g(x)
= С,
g(x) = F1(x) - F(x) випливає, що F1(x) – F(x) = С, або F1(x) = F(x) + С.
Основній властивості первісної можна надати геометричного змісту: графіки будь-яких двох первісних для функції f одержуються один із одного паралельним перенесенням вздовж осі ΟΥ (рис. 87).
