Доведення

Нехай дано дві точки А(x_A, у_A, z_A) і В(х_B, y_B, z_B) (рис. 254). Доведе­мо, що

АВ² = (х_B – x_A)² + (y_B – у_A)² + (z_B – z_A)².

Розглянемо випадок, коли АВ не паралельна осі z. Через точки А і В проведемо прямі, паралельні осі z. Вони перетнуть площину ху в точках A₁ і В₁ відповідно. Ці точки мають ті самі координати х, у, що й точки А і В, а координата z їх однакова і дорівнює нулю. Проведемо через точку А площину, паралель­ну координатній площині ху. Побудована площина перетне пряму ВВ₁ у деякій точці С, причому ВС = | z_B – z_A|. За теоремою Піфагора із ΔАВС маємо:

АВ² = AC² + ВС². Оскільки АС² = A₁В₁² = (х_B – x_A)² + (y_B – у_A)² ,

ВС = | z_B – z_A |, то АВ² = (х_B – x_A)² + (y_B – у_A)² + (z_B – z_A)².

Таким чином, відстань між точками А(x_A, у_A, z_A) і В(х_B, y_B, z_B) обчислюється за формулою .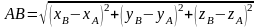

Білет № 16

1. Тригонометричні рівняння. Розв’язування рівнянь виду: sin x = a, cos x = a.

2. Правильна піраміда, Площа бічної поверхні правильної піраміди.

3. Знайти проміжки, на яких функція f(x) = x³ – x² – 5x – 3 зростає, спадає

4. Основа піраміди – квадрат зі стороною 12 см, а дві суміжні бічні грані перпендикулярні до площини основи. Обчисліть площу бічної поверхні піраміди, якщо її висота дорівнює 5 см.

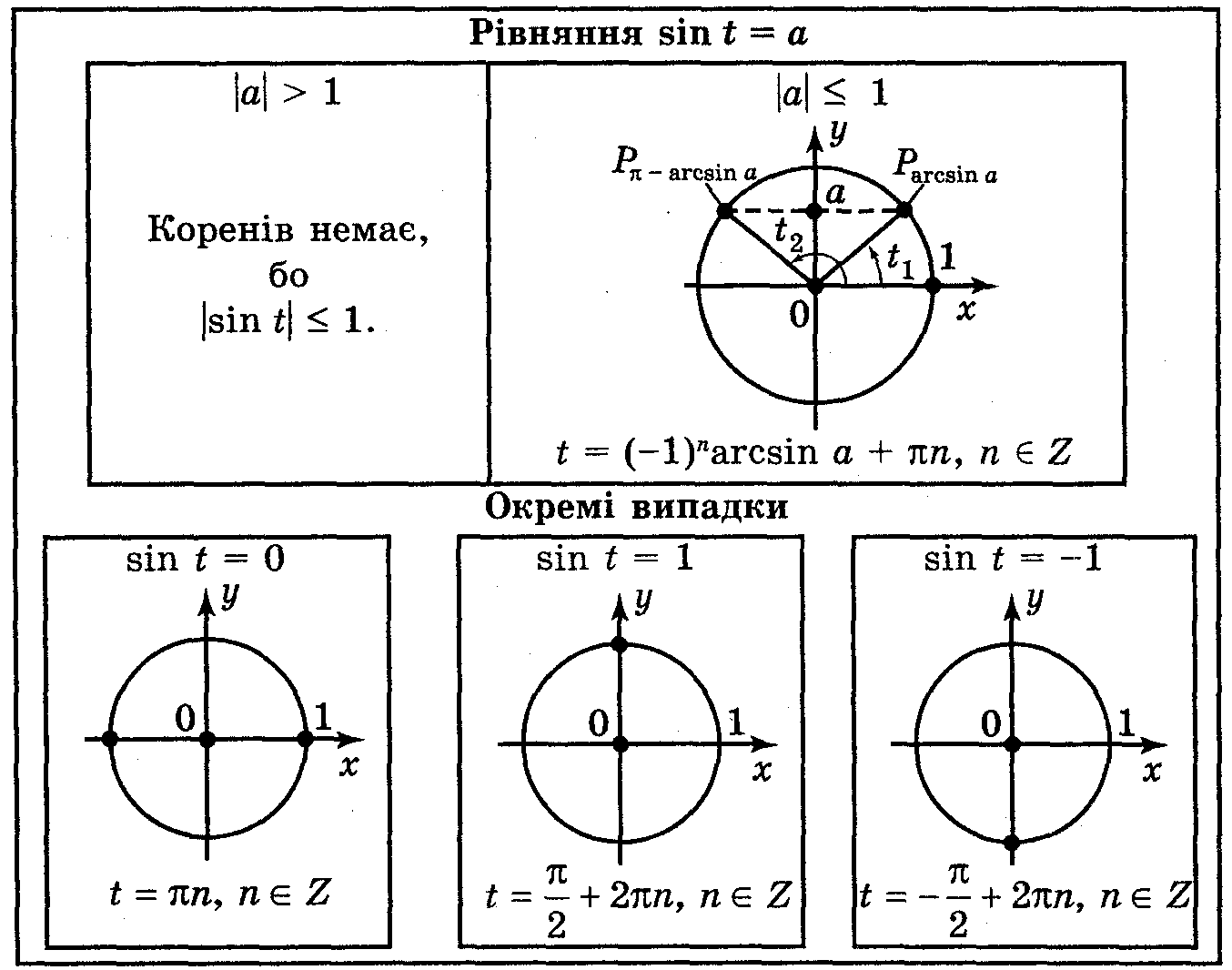
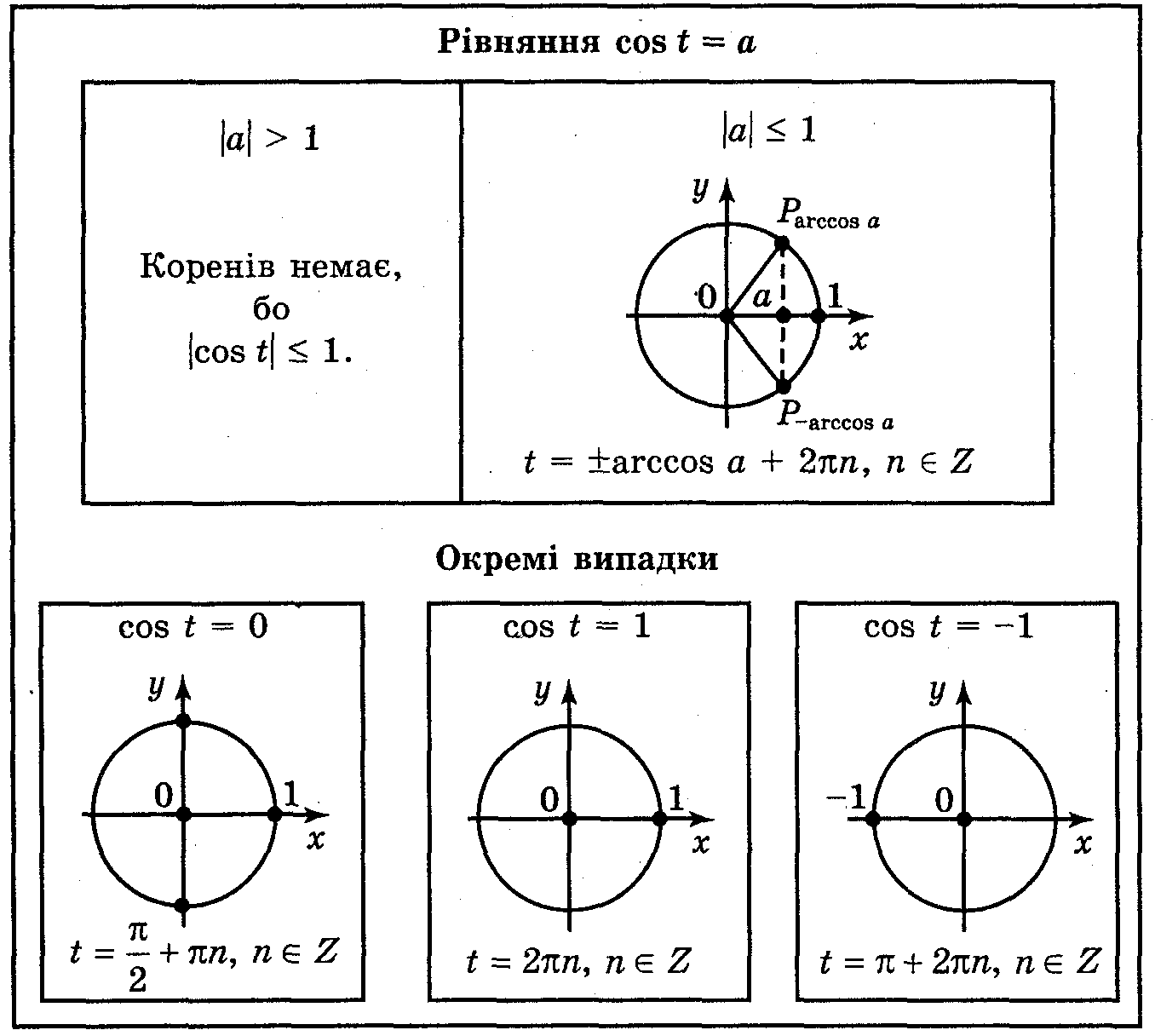
1. Тригонометричні рівняння. Розв’язування рівнянь виду: sin x = a, cos x = a.

Рівняння називаються тригонометричними, якщо змінна величина знаходиться під знаком тригонометричної функції. Найпростішими тригонометричними рівняннями називаються рівняння виду:

sin x=a; cos x=a; tg x=a; ctg x=a.

2. Правильна піраміда, Площа бічної поверхні правильної піраміди.

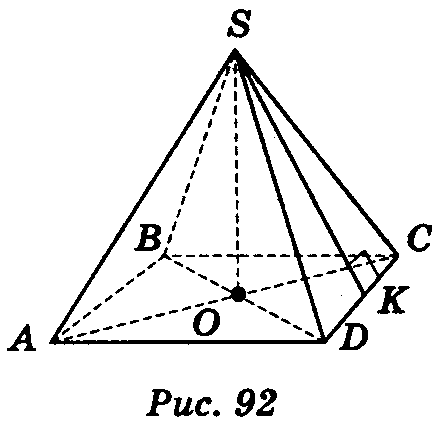
Правильною пірамідою називається піраміда, в основі якої ле­жить правильний многокутник, а основа висоти піраміди збігається з центром цього многокутника.

Нехай SАВСD — правильна чотирикутна піра­міда (рис. 92). Тоді за означенням її основа АВСD — правильний чотирикутник (квадрат); центр квад­рата точка О — основа висоти S0 піраміди.

Пряма, яка містить висоту піраміди, на­зивається віссю правильної піраміди. Висота бічної грані правильної піраміди, яка проведена з вершини піраміди, назива­ється апофемою. На рис. 92 SК — апофема.

У правильної піраміди:

1. бічні ребра рівні;

2. бічні грані рівні;

3. апофеми рівні;

4. двогранні кути при основі рівні;

5. двогранні кути при бічних ребрах рівні;

6. кожна точка висоти правильної піраміди рівновіддалена від всіх ве­ршин основи;

7. кожна точка висоти правильної піраміди рівновіддалена від усіх бічних граней.

Теорема. Площа бічної поверхні правильної піраміди дорівнює добутку півпериметра її основи на апофему.

Доведення

Нехай а — сторона основи правильної п-кутної піраміди (рис. 255). SH BC, SH = m.

Тоді площа бічної грані правильної піраміди дорівнює 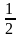am, а площа бічної поверхні S_бічн = атп. Оскільки ап = р, де р — півпериметр основи піраміди, то S_бічн = pm.

Білет № 17

1. Тригонометричні рівняння. Розв’язування рівнянь виду: tg x = a, ctg x = a.

2. Конус. Формули об’єму конуса та площі повної поверхні конуса.

3. Дослідіть функцію f (x) = x⁴ –4x² та побудуйте її графік.

4. Через дві твірні конуса, кут між якими дорівнює α, проведено переріз, який утворює з площиною основи конуса кут β . Знайдіть площу бічної поверхні конуса, якщо його висота рівна Н.

1. Тригонометричні рівняння. Розв’язування рівнянь виду: tg x = a, ctg x = a.

Рівняння називаються тригонометричними, якщо змінна величина знаходиться під знаком тригонометричної функції.

Найпростішими тригонометричними рівняннями називаються рівняння виду:

sin x=a; cos x=a; tg x=a; ctg x=a.