Білет № 1

1. Дійсні числа. Дії над дійсними числами.

2. Об’єм кулі та її частин.

3. Побудувати графік функції f(x) = .

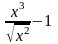4. Основа піраміди – ромб з гострим кутом і більшою діагоналлю d. Усі бічні грані піраміди нахилені до площини основи під кутом . Знайдіть об’єм піраміди.

1. Дійсні числа. Дії над дійсними числами

Всі числа можна поділити на :

1. Натуральні (N) - це ті, які використовуються при лічбі. Для їх запису потрібно 10 цифр ( 0 – 9);

2. Цілі числа (Z ) – це число від’ємні, нуль, додатні натуральні;

3. Дійсні числа ( R ) – раціональні та ірраціональні числа

R (дійсні числа)

раціональні ірраціональні

( це ті, які можна представити (це ті, які можна представити нескінченним,

десятковим дробом) періодичним, десятковим дробом)

Дії над числами:

1. Порівняння дійсних чисел: число 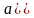, якщо воно розташовано лівіше на координатній прямій. Наприклад, 148>-2489, 214<6500.

2. Сумою двох дійсних чисел 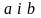називається число 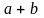, що задовольняє умовам:

1). Сума додатних чисел є число додатне; наприклад, 123+56=179

2). Сума від’ємних чисел є число від’ємне: додаємо модулі доданків і в переді ставимо знак мінус; наприклад, -12+(-45)=-57.

3). Сума чисел з різними знаками - це число, яке має знак такий, як і доданок з більшим модулем, а модуль суми – це різниця між доданками з більшим і меншим модулем, наприклад, 96+(-54)=42, -56+48=-8.

3. Добутком чисел є число 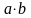, яке задовольняє умовам:

1). Добуток додатних чисел є число додатне, наприклад,

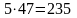
2). Добуток від’ємних чисел є число додатне; наприклад,

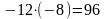
3). Добуток чисел з різними знаками є число від’ємне, наприклад, .

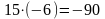4. Віднімання і ділення – це дії, обернені додаванню і множенню.

2. Об’єм кулі та її частин

Об’єм кулі визначається за формулою:

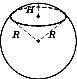V = 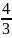πR³, де R - радіус кулі.

Кульовим сегментом називається частина кулі, яка відсікається від кулі площиною.

Об’єм кульового сегменту дорівнює:

V = π Н² ( R - ),

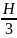де Н - висота кульового сегмента,

R — радіус кулі.

Кульовим сектором називається тіло, яке одержуємо з кульового сегменту і конусу таким чином: якщо кульовий сегмент менший від півкулі, то кульовий сегмент доповнюється конусом, у якого вершина в центрі кулі, а основою є основа сегмента.

Якщо ж сегмент більший від півкулі, то конус із нього виймається.

Об’єм кульового сектору одержуємо додаванням або відніманням відповідних сегмента і конуса.

Об’єм кульового сектора знаходимо за формулою:

V = 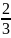πR²Н,

де R — радіус кулі,

H — висота відповідного кульового сегмента

Білет № 2

1. Радіанне вимірювання кутів. Тригонометричні функції числового аргументу.

2. Об’єм циліндра і конуса.

3. Знайдіть найбільше і найменше значення функції на даному проміжку:

f(x) = 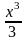- 3x² + 5x - 7 на [-1; 3].

4. В урні лежать 20 кульок, з яких 12 білих, решта - чорні. З урни навмання виймають дві кульки. Яка ймовірність того, що вони білі?

1. Радіанне вимірювання кутів. Тригонометричні функції числового аргументу.

Як відомо, кути вимірюються в градусах, хвилинах, секундах,

Градусом називається 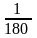частина розгорнутого кута.

Таким чином, розгорнутий кут дорівнює 180°, прямий кут дорівнює 90°.

М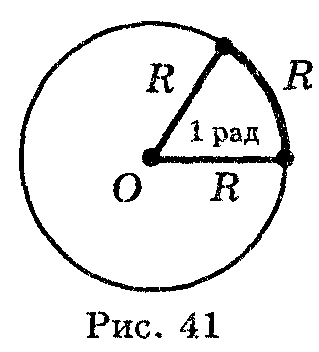 іж градусами, хвилинами і секундами існують співвідно­шення: 1º = 60', 1' = 60'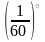', 1' = , 1' = 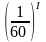. Крім градусної міри, використовуються і інші одиниці вимі­рювання кутів. У математиці і фізиці - це радіанна міра кута.

1 радіан — центральний кут, який опирається на дугу, довжина якої дорівнює радіусу(рис. 41).

К уту, що дорівнює 180°, відповідає півколо, тобто дуга, довжина якої дорівнює πR (рис. 42). Щоб знайти радіанну міру кута в 180°, треба довжину дуги πR розділити на

довжину радіуса R: 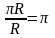. Отже, радіанна міра кута в 180° дорівнює π: 180° = π рад

Із цієї формули одержуємо (розділивши ліву і праву частини рівності на 180):

1° = 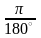рад, або 1° 0,017 рад.

Із рівності 180° = π рад також одержуємо (розділивши ліву і праву частини рівності на π):

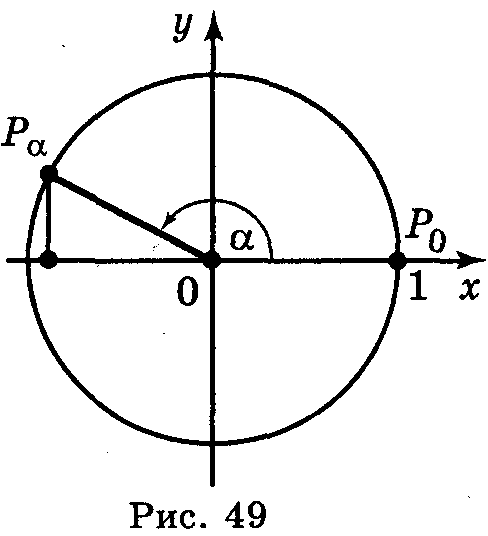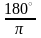1 рад = , або 1 рад 57°.

Синусом числа α називається ордината точки Р_α, утвореної пово­ротом точки Р_α (1; 0) навколо початку координат на кут в α раді­ан (позначається sin α) (рис. 49).

Синус визначений для будь-якого числа α.

Косинусом числа α називається абсциса точки Р_α, утвореної по­воротом точки Р_α (1; 0) навколо початку координат на кут в α радіан (позначається cos α) (рис. 49).

Косинус визначений для будь-якого числа α.

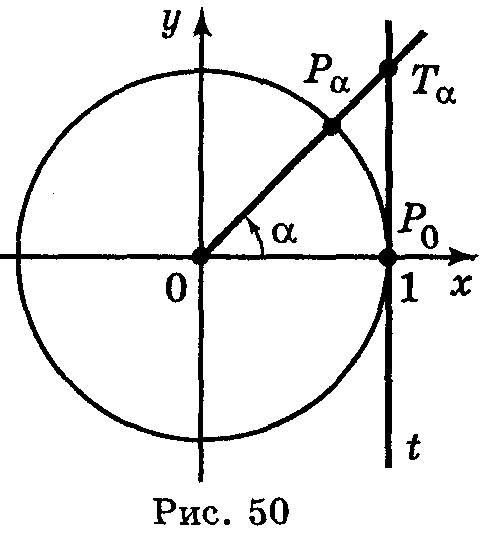
Тангенсом числа α називається відношення синуса числа α до його косинуса: .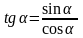

Ордината точки перетину прямих ОР_α і t дорівнює тангенсу числа α. Тому пряму t нази­вають віссю тангенсів.

Котангенсом числа α називається від­ношення косинуса числа α до його синуса: .

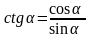Абсциса точки перетину прямої ОР_α і q дорівнює котангенсу числа α, тому пряму q називають віссю котангенсів.