
 ФЕДЕРАЛЬНОЕ
АГЕНСТВО ПО ОБРАЗОВАНИЮ.
ФЕДЕРАЛЬНОЕ
АГЕНСТВО ПО ОБРАЗОВАНИЮ.
Государственное образовательное учреждение высшего профессионального образования.
«Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» имени В.И. Ульянова (Ленина)»
(СПБГЭТУ)

Кафедра ВТ
Практическая работа №7
«Исследование методов безусловной оптимизации первого порядка»
Выполнил: ст. группы 9307 Джабаров Р.Р.
Проверил: проф. Дмитревич Г.Д.

Санкт-Петербург
2014 г.
Оглавление
Задание. 2
Описание методов оптимизации. 2
Спецификация программы. 4
Результаты тестирования программы 6
Ответы на контрольные вопросы 6
Задание.
Целью работы является изучение методов сопряженных градиентов и методов с переменной метрикой
Описание методов оптимизации.
Метод трехточечного поиска на равных интервалах
В практических задачах вычисление производной на каждой итерации может оказаться затруднительным, а иногда и просто невозможным. Рассматриваемый метод позволяет сократить интервал локализации минимума на основе сравнения значений функции в пробных точках без вычисления производных.
Начальный этап (1) Задать [a1, b1] - начальный интервал поиска, где a1, b1 - границы интервала, удовлетворяющие условию f (a1)f (b1)<0; - погрешность вычисления минимума х*. (2) Положить xm = (a1 + b1)/2 и k = 1.
Основной этап
Шаг 1. Взять две пробные точки x1 = ak + Lk/4 и x2 = bk - Lk/4, где Lk = bk - ak - длина текущего интервала. Точки х1, х2 и хm делят [ak, bk] на четыре равные части.
Шаг 2. Сократить текущий интервал локализации минимума:
(1) если f1 < fm, то положить ak+1 = ak, bk+1 = xm, xm = x1, перейти на шаг 3;
(2) если f1 ≥ fm ≤ f2, то положить ak+1 = x1, bk+1 = x2; иначе - ak+1 = xm, bk+1 = bk, xm = x2.
Шаг 3. Проверить критерий окончания поиска:
(1) заменить k на k +1;
(2) если Lk = bk - ak ≤ , то остановиться. Если данное условие не выполняется, вернуться на шаг 1.
Метод Полака-Рибьера
Метод Полака-Рибьера является разновидностью метода Флетчера-Ривза. Ниже приводятся операции этого алгоритма:
Шаг
1. В
 вычисляется
вычисляется
 .
.
Шаг
2. На k-м
шаге с помощью одномерного поиска в
направлении
 ,
находим минимум
,
находим минимум
 .
Это определяет точку
.
Это определяет точку
 .
.
Шаг
3. Вычисляются
 и
и
 .
.
Шаг
4. Направление
 определяется из соотношения
определяется из соотношения
 (4.5)
(4.5)
После
(n+1)
итерации (k=n)
процедура циклически повторяется с
заменой
 на
на
 .
.
Шаг
5. Алгоритм заканчивается, когда
 ,
где
,
где
 - произвольная константа.
- произвольная константа.
Спецификация программы.
В программе использовался метод сопряженных градиентов – “метод Полака-Рибъера”, а также метод одномерного поиска – “Метод трехточечного поиска”.
Текст программы
// bn.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <stdio.h>
#include <iostream>
#include <conio.h>
#include <math.h>
using namespace std;
double icount =1;
double icountz=1;
double x0[2] = {0,3}, p[2];
double f(double x1, double x2) {
return (x1-2)*(x1-2)*(x1-2)*(x1-2) + (x1-2*x2)*(x1-2*x2);
}
double y (double alfa) {
return f (x0[0]+p[0]*alfa,x0[1]+p[1]*alfa);
}
double norm (double x[2]) {
return sqrt(x[0]*x[0] + x[1]*x[1]);
}
void swann( double x, double& a, double& b, double h = 0.0001) {
int k;
if( y(x) < y(x+h) )
h *= -1;
for( k=0; y(x+h) < y(x); k++ ) {
h *= 2;
x += h;
}
if(h>0)
{
a=x-h;
b=x+h;
}
else
{
a=x+h;
b=x-h;
}
if( icount )
icount = k;
}
double three_point_search( double a, double b, double eps = 0.0001, int* icount = NULL ) {
double L, x_m = (a + b)/2, x_1, x_2;
int k;
for( k=0; abs(b - a) > eps; k++ ) {
L = abs(b - a);
x_1 = a + L/4;
x_2 = b - L/4;
if( y(x_1) < y(x_m) ) {
b = x_m;
x_m = x_1;
}
else if( y(x_m) <= y(x_1) && y(x_m) <= y(x_2) ) {
a = x_1;
b = x_2;
}
else {
a = x_m;
x_m = x_2;
}
}
if( icountz )
icountz = k;
return x_m;
}
void VecCopy ( double dst[2], double src[2]) {
dst[0] = src [0];
dst[1] = src [1];
}
double dif (double x[2], int nom, double h = 0.0001) {
if (nom == 0) {
return ( f(x[0] + h, x[1]) - f(x[0] - h, x[1]))/(2*h);
}
else
return ( f(x[0], x[1] + h) - f( x[0], x[1] - h))/(2*h);
}
double polaka_ribera (void) {
int k = 1;
double g [2];
double glast [2], beta, betaz ;
while (1) {
g[0] = dif(x0,0);
g[1] = dif(x0,1);
if (k%2) {
VecCopy ( p, g);
}
else {
beta = g[1]*(g[1]-g[0])/(glast[0]*glast[0]);
betaz = g[1]*(g[1]-g[0])/(glast[1]*glast[1]);
p[0] = - g[0] - beta*p[0];
p[1] = - g[1] - betaz*p[1];
}
VecCopy (glast,g);
double a, b;
swann( 0,a, b ); //работаем с одномерным пространством
double alpha = three_point_search( a, b ); //работаем с одномерным пространством
x0[0] = x0[0] + p[0]*alpha; //получаем векторные значения
x0[1] = x0[1] + p[1]*alpha;
if (abs(norm(g)) < 0.0001)
return alpha;
}
}
int main (void) {
double alpha = polaka_ribera();
cout << "Minimum function" ; cout << endl;
cout << (x0[0] + p[0]*alpha) ; cout << endl;
cout << (x0[1] + p[1]*alpha); cout << endl;
cout <<"Kol-vo Iteracii methoda trehtochechnogo poiska:" << icount; cout << endl;
getch();
return 0;
}
Результаты тестирования программы
|
Точность |
0.001 |
|
|
|
|
|
|
Метод Полака-Рибьера |
11- метод одномерного поиска |
x=[2;1] |
Ответы на контрольные вопросы
1. Определить характер матрицы Гессе функции y(x) = (x2 – x1)2 + + (1 – x1)2 в точке минимума x* = (1; 1)t. Используя матрицу Гессе найти направление, сопряженное к p = (1; 0)t.
G= =>H=
=>H=
P1*H*p2=0
=>

Пусть
y=2
=> x=1
=> p2=
-
Являются ли направления p1 = (0; 1)t и p2 = (1; 0)t линейно независимыми? Ортогональными? Сопряженными?
Данные вектора являются ортогональными =>независимы
P1*p2=0*1+1*0=0-Ортогональные
P1*H*p2= - Сопряженные
- Сопряженные
е
-
Дана функция y(x) = x12 + x22 + x32 и точка xk = (1; 2; 3)t. Определить точку xk + 1 методом Даниела.
Ш1:
p1=-g1= =
=
Ш2:
x2= =>f(a1)=(1+2*a1)^2+(2+4*a1)^2+(3+6*a1)^2
=>f(a1)=(1+2*a1)^2+(2+4*a1)^2+(3+6*a1)^2
F’(a1)=4(1+2*a1)+ 16(1+2*a1)+36*(1+2*a1)=0 => a1=1/2
Ш3:
x2=
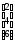 Ш4:
||g1||=(4+16+36)^1/2 > E
Ш4:
||g1||=(4+16+36)^1/2 > E
-
Используя метод сопряженных градиентов найти точку xk + 1 для функции y(x) = x12 + 2x1x2 + x22 и xk = (1; 1; 1)t.
Ш1:
p1=-g1= =
=
Ш2:
x2= =>f(a1)=(1+4*a1)^2+2*(1+4*a1)*(1+4*a1)+(1+4*a1)^2
=>f(a1)=(1+4*a1)^2+2*(1+4*a1)*(1+4*a1)+(1+4*a1)^2
F’(a1)=32*(1+4*a1) =0 => a1=1/4
Ш3:
x2=
 Ш4:
||g1||=(4+4+1)^1/2=3
> E
Ш4:
||g1||=(4+4+1)^1/2=3
> E
Вывод.
Были изучены методы сопряженных градиентов и разработана программа, описывающая эти методы.


