2.2 Причины образования погрешностей результатов измерений

Погрешности измерений в зависимости от их происхождения могут быть разделены на три класса: систематические погрешности, промахи, случайные погрешности. Грубые погрешности (промахи) вызываются неправильностью отсчета по шкале измерительного прибора, неверной записью отчетов, неправильным использованием приборов и т. п. В любом случае результат, искаженный промахом, необходимо исключить из ряда измерений.

Случайными погрешностями называются погрешности, которые непредсказуемым образом изменяют свою величину и знак от опыта к опыту. Правила определения случайных погрешностей рассматриваются в теории погрешностей, основанной на теории вероятностей, позволяющей по данным измерений вычислить наиболее вероятное значение измеренной величины и оценить погрешностей измерений.

Систематическими погрешностями называются погрешности постоянные или изменяющиеся по определенному закону. Систематические погрешности вызываются большей частью неправильностью показаний самих приборов или самим методом измерений , или, наконец, постоянным, но односторонним внешним воздействием.

Имеется ряд слагаемых погрешностей, которые являются доминирующими в общей погрешности измерения. К ним относятся:

Погрешности, зависящие от средств измерения. Нормируемую допустимую погрешность измерительного средства следует рассматривать как погрешность измерения при одном из возможных вариантов использования этого измерительного средства, поскольку проверка точности данных приборов заключается чаще всего в измерении им эталона.

Погрешности, зависящие от установочных мер. Установочные меры могут быть универсальными (концевые меры) и специальными (изготовленными по виду измеряемой детали). Погрешность измерения будет меньше, если установочная мера будет максимально подобна измеряемой детали по конструкции, массе, материалу, его физическим свойствам, способу базирования и т.д. Погрешности от концевых мер длины возникают из-за погрешности изготовления (классы) или погрешности аттестации (разряды), а также из-за погрешности их притирки.

Погрешности, зависящие от измерительного усилия. При оценке влияния измерительного усилия на погрешность измерения необходимо выделить упругие деформации установочного узла и деформации в зоне контакта измерительного наконечника с деталью.

Погрешности, происходящие от температурных деформаций (температурные погрешности). Погрешности возникают из-за разности температур объекта измерения и измерительного средства. Существуют два основных источника, обуславливающих погрешность от температурных деформаций: отклонение температуры воздуха от 20^о С и кратко-временные колебания температуры воздуха в процессе измерения.

Максимальное влияние отклонений температуры на погрешность измерения l_t можно рассчитать по формуле

l_t1 = lt₁(_п - _д)_max ,

где t₁ - отклонение температуры от 20^оС;

_п , _д - коэффициенты линейных расширений прибора и детали.

Максимальное влияние кратковременных колебаний температуры среды на погрешность измерения будет иметь место в том случае, если колебания температуры воздуха не вызывают изменений температуры

измерительного средства, а температура объекта измерения близко следует за температурой воздуха (или наоборот)

l_t2 = lt₂_max ,

где t₂ - кратковременные колебания температуры воздуха в процессе измерения;

_max - наибольшее значение коэффициента линейного расширения (материала прибора или измеряемой детали).

Общая деформация по двум случайным составляющим t₁ и t₂ выразится формулой

Могут возникнуть и дополнительные деформации при использовании накладных приборов.

Погрешности, зависящие от оператора (субъективные погрешности). Возможны четыре вида субъективных погрешностей:

Погрешность отсчитывания (особенно важна, когда обеспечивается погрешность измерения, не превышающая цену деления); погрешность присутствия (проявляется в виде влияния теплоизлучения оператора на температуру окружающей среды, а тем самым и на измерительное средство); погрешность действия (вносится оператором при настройке прибора); профессиональные погрешности (связаны с квалификацией оператора, с отношением его к процессу измерения).

Погрешности при отклонениях от правильной геометрической формы. При измерении деталей с целью учёта возможной погрешности формы рекомендуется:

измерение производить в нескольких точках (как правило в шести);

Случайные погрешности имеют статистический характер, их математическая обработка производится с помощью теории вероятностей. При многократном измерении равновероятно получить результат как большой, так и меньший , чем истинное значение измеряемой величины.

Пусть проведено n измерений величины х и в результате получено n значений : х₁; х₂;…; х_n. При обработке полученных результатов возникают два вопроса: 1) как получить из этих значений наиболее вероятное значение измеряемой величины; и 2) чему равна ожидаемая ошибка измерений?

Ответ на эти вопросы дает теория вероятностей.

Наиболее вероятным (действительным) значением измеряемой величины является среднее арифметическое значение, найденное в результате измерений

Физический смысл формулы (1) состоит в том, что при вычислении среднего арифметического ошибки в сторону преувеличения и преуменьшения результата наилучшим образом компенсируют друг друга.

Обратимся ко второму вопросу: к оценке ошибок измерений. Для уяснения этого вопроса построим график распределения ошибок. По оси абсцисс будем откладывать величину ошибок, допущенных в разных опытах. Разобьем эту ось на ряд равных интервалов , ширина которых может быть любой и выбирается из соображений удобства.

По оси ординат отложим число случаев , когда ошибка попала в данный интервал. При этом лучше использовать не абсолютное значение m, а относительное . В результате получаем ступенчатую кривую, которая называется гистограммой.

Максимум гистограммы находится в области небольших ошибок (очень большие ошибки при разумной постановке опыта происходят крайне редко). Такая кривая называется кривой распределения случайной величины, а функция , описывающая эту кривую, плотностью вероятности.

Существует относительно много законов распределения случайных величин. Однако особое значение в теории вероятностей и в практике измерений имеет нормальный закон распределения случайной величины, для которого плотность распределения описывается формулой Гаусса

,

где - среднее арифметическое значение случайной величины; - средняя квадратичная погрешность.

Величина, распределенная по нормальному закону, имеет множество значений, поэтому нормальное распределение удобно изображать графически. Плотность распределения подчиняется условиям нормировки. , т.е. вероятность того, что ошибка имеет произвольное значение, равна единице – достоверное событие. Обычно ошибки разных знаков равновероятны, т.е.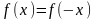 . Чем больше ошибка по вероятной величине, тем меньше ее вероятность, т.е. монотонно убывает при возрастании х.

Таким образом, площадь под всей кривой понимается равной единице. Площадь, отвечающая какому-либо интервалу оси абсцисс, изображает вероятность попадания случайного результата в данный интервал. Основная масса получаемых результатов будет группироваться около некоторого среднего значения измеряемой величины. На участке от до размещается в среднем 68% всех произведенных измерений. Величина носит название стандартного отклонения или стандартной ошибки. В границах более широких ( ) размещается в среднем 95% всех измерений, а на участке ( ) – 99,7%. За трехсигмовые пределы выходит ничтожная доля всего числа измерений. Величина представляет собой максимальную погрешность результата измерений.

При большом количестве измерений n одной и той же величины согласно теории вероятностей средняя квадратичная (стандартная) ошибка рассчитывается по формуле

,

где - значение, полученное в -ом опыте, - число опытов, - среднее арифметическое .

Рассматриваемый метод справедлив при большом количестве измерений одной и той же величины. На практике, как правило, обычно имеют дело с рядами, содержащими довольно ограниченное число измерений. В 1908 Боссет (псевдоним “Стьюдент”) установил правила, на основании которых можно производить обработку результатов измерений при малом количестве измерений. В этом случае вместо рассматривают ее приближенное значение

При этом

Назовем абсолютной погрешностью результата измерений , где - истинное значение. Эта погрешность зависит от числа измерений и является случайной величиной. Непосредственно вычислить ее невозможно. Но теория Боссета дает возможность рассчитать значение абсолютной погрешности, если известна доверительная вероятность, с которой необходимо выполнить эксперимент

где - коэффициент Стьюдента. Численные значения этого коэффициента в зависимости от числа измерений и заданной доверительной вероятности приведены в таблице приложения.

Среднее квадратичное отклонение силы тока

Среднее квадратичное отклонение напряжения:

Тогда находим случайную составляющую погрешности измерения силы тока

Находим случайную составляющую погрешности измерения напряжения

С учетом систематических ошибок полная абсолютная ошибка при прямых измерениях может быть рассчитана по формуле:

,

Где Δх – случайная составляющая погрешности,

Δ – погрешность прибора (определяемая его классом точности).

Для силы тока

Для напряжения

После нахождения среднего арифметического значения измеряемой величины и ее абсолютной погрешности при известной доверительной вероятности окончательный результат можно записать в виде:

при заданном

т.е. истинное значение величины находится в доверительном интервале от до с вероятностью . Чем меньше интервал, в котором находится истинное значение измеряемой величины при неизменной доверительной вероятности, тем лучше справился экспериментатор со своей задачей.

Следует отметить, что абсолютная погрешность не является достаточной характеристикой качественности проведения эксперимента. Количественной характеристикой точности проведенных измерений является относительная погрешность