Министерство образования Российской Федерации

Филиал Северного Арктического Федерального Университета

Севмашвтуз Кафедра математики

Черткова Ольга Владимировна

Методические указания

К выполнению контрольной работы №3

По “Линейной алгебре ”

Для заочного обучения

1. Методические указания к контрольной работе №3 по теме: «Линейные пространства».

1.1ЗАДАНИЕ №1.

Для выполнения этого задания студент обязан чётко владеть понятиями линейного пространства и евклидова пространства и применять эти понятия к различным совокупностям математических объектов.

Определение №1. Не пустое множество L элементов любой природы называются вещественным линейным пространством, если выполнены следующие требования:

1. Имеется правило, посредством которого любым двум элементам х

и у множества L ставится в соответствие третий элемент z этого же множества, называемый суммой элементов х и у и обозначаемый

z = x + y

2. Имеется правило, посредством которого любому элементу x

множества L и любому вещественному числу ставится в соответствие y этого же множества, называемый произведением элемента x на число и обозначаемый

3. Указанные правила подчинены следующим аксиомам:

1⁰. x+y=y+x

2⁰. (x+y) + z = x + (y+z)

3⁰. Существует нулевой элемент 0. Такой что

x + 0=x, для любого элемента x

4⁰. Для каждого элемента x существует противоположный элемент

x^-1 такой что, x+x^-1 = 0

5⁰. 1 x = x

6⁰.

7⁰.

8⁰.

Замечание при определении умножения вместо поля вещественных

чисел можно взять любое поле K, однако в контрольной работе речь идёт о вещественном линейном пространстве.

Пример №1. Доказать, что матрицы вида образуют линейное пространство. Найти его размерность и базис.

Решение: Пусть правила произведения и суммы определены обычным образом: =

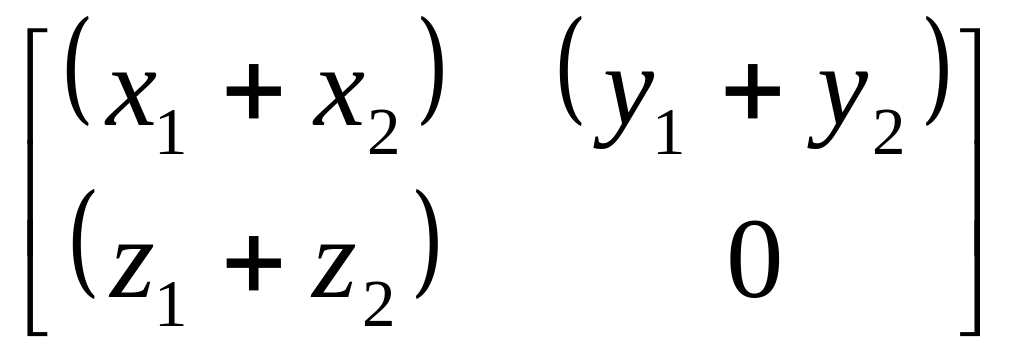
и

Очевидно, что результаты операций принадлежат этого же вида.

Поскольку сложение матриц коммутативно ассоциативно, то аксиомы 1⁰ и 2⁰ не подлежат сомнению.

1⁰.

2⁰.

3⁰. Нулевым элементом назовём

, действительно

4⁰. Противоположным элементом назовём

, действительно

5⁰.

6⁰.

7⁰.

8⁰.

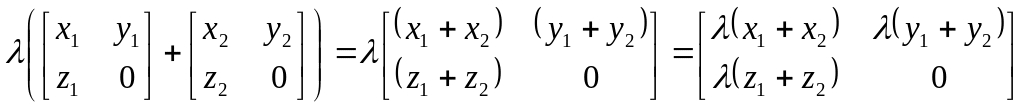
Очевидно, что каждую матрицу вида можно единственным образом представить в виде линейной комбинации:

=

Т.о. Базис этого пространства составляют матрицы

, а dim L=3

Определение №2. Вещественное линейное пространство L называется вещественным евклидовым, если выполнены следующие требования:

1. Имеется правило посредством которого любым двум элементам x и y

пространства L ставится в соответствие вещественное число, называемое скалярным произведением этих элементов и обозначаемое (х,у).

2. Указанное правило подчиняется аксиомам:

1⁰.

2⁰.

3⁰.

4⁰. >0,если x-не нулевой элемент; (x,x)=0, если x-нулевой элемент.

Пример №2. Доказать, что в пространстве функций непрерывных на отрезке а, b скалярное произведение функции f(x) и g(x) нельзя задать как приращение производной от их произведения, т.е.

(f(x),g(x))=

Проверим аксиомы из определения евклидова пространства

1. (f(x),g(x))= = =(g(x),f(x))

2)

3) = = =[т.к. , то]=

4)

невозможно сделать выводов относительно знака этого выражения для поризводной f(х) , следовательно

Последняя аксиома не выполнена, следовательно, формула не может быть использована для задания скалярного произведения в линейном пространстве функций непрерывных на а,b.