Билет №1

1. Регрессионные модели идентификации: статический объект, понятия о регрессии, парная и множественная регрессия, ошибка идентификации.

Объект считается статическим, если находится в установившемся (стационарном) состоянии. Модель статического объекта связывается установившимися значениями входных и выходных сигналов.

Регрессионные модели идентификации

, .

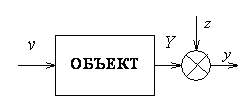
Рассматривается объект с n – наблюдаемыми входами и одним выходом. Кроме того, на выход объекта оказывают влияние ненаблюдаемые входы z. Нельзя говорить о функциональной зависимости между выходом и наблюдаемыми входами, а можно говорить о стохастичности или вероятностной связи.

Упростим задачу, рассматривая объект одним входом и одним выходом . Будем задавать случайный вход и фиксировать выход.

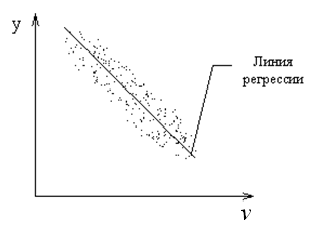
Получаем множество точек с координатами – корреляционное поле.

Для одного и того же значения входа – множество выходов (выход подвержен влиянию ненаблюдаемых входов). Действие ненаблюдаемых входов z можно интерпретировать как влияние помехи.

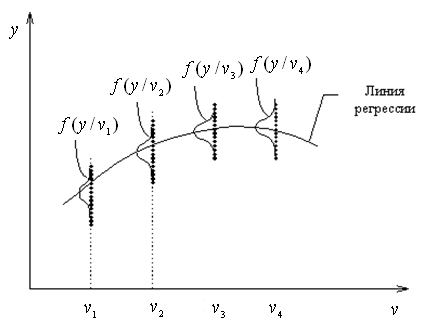
Для того, чтобы установить связь между выходом и входом рассмотрим рисунок

Множество выходов можно заменить средним значением

(1) где - условная плотность вероятности выхода при данном значении .

Зависимость называется регрессионной:

Соединяя средние точки кривой, получим регрессию . Регрессионная зависимость представляет собой статическую характеристику ОУ.

Если ОУ имеет один вход и один выход, то его характеристикой является простая или парная регрессия: . Если математическое ожидание выхода связно n – входами, то регрессия множественная: В литературе вектор входов называют точкой в факторном пространстве, а – поверхность отклика в факторном пространстве.

Как простая регрессия, так и множественная, являются моделями статического объекта (с одним и n – входами).

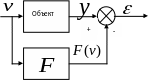
Значение выхода: (2) где – фактическое значение результативного признака (выхода ОУ); – теоретическое значение выхода ОУ, найденное из уравнения регрессии; – случайная величина, обусловленная действием ненаблюдаемых факторов ОУ.

Графически (2) представлено в виде схемы на рис выше.

Мера близости модели и объекта определяется некоторым функционалом ошибки: который зависит от структуры модели вектора параметров.

Оценка модели выполняется на основе минимизации или снижения до определенного уровня значения . Одним из критерия идентификации является критерий качества (4):

(4) Согласно которому оператор можно принять за модель объекта, если максимальное значение модуля ошибки идентификации на интервале наблюдений стремится к минимальной величине. Критерий (4) используется, если входы и выход объекта являются детерминированными функциями(неслучайными). Но, как правило, входные воздействия являются случайными сигналами, поэтому используется критерий (5):   (5)

Выбирается та модель, которая приводит математическое ожидание в минимум. Для практики используется квадратичный критерий качества, значения которых всегда неотрицательны. Для детерминированных сигналов – критерий (6), для аналоговых – критерий (4).

, (6)

Для случайных сигналов – критерий (7):

. (7)

. (8)

Критерий (8) используется, если выходы объекта и модели являются непрерывными функциями (функциями с непрерывным временем), если измерение осуществляется дискретно, то используется критерий (9):

(9)

В случаях 4-9 минимизация осуществляется по оператору . Изменяем структуру и параметры операторов и выбирается с минимальной ошибкой.

Для нахождения оценки коэффициентов определяем ошибку идентификации:

– остаточный ряд,

где - вектор невязок (остатков).

– дисперсия остатка, – единичная матрица, – ковариационная матрица остатков, элементами которой являются ковариации между остатками, а по главной диагонали дисперсии.

Для нахождения оценок коэффициентов регрессии введем критерий идентификации в виде квадрата нормы остатков:

(6)

В качестве оценок выбирают такие величины, при которых . (6) – оптимизационная задача без ограничений, т.е. может быть любым.

Находится векторная производная от целевой функции и приравнивается к нулю:

– матричное уравнение.

В результате получим

(7)