Основные положения кинетической теории

В основе кинетической теории газов лежат следующие положения:

1. Все тела состоят из большого количества атомов и молекул, движущихся в случайных направлениях с различными скоростями,

2. Расстояния между молекулами значительно превышают размеры самих атомов или молекул,

3. Движение каждой молекулы подчиняется законам классической механики.

4. Взаимодействие молекул между собой носит характер упругих столкновений.

Газ, который удовлетворяет всем этим требованиям, называется идеальным.

В нормальных условиях (давление p₀ =10⁵ Н/м² , температура T₀= 273 К) поведение большинства реальных газов может достаточно точно описываться законами идеального газа, но при сильных сжатиях конечный размер молекул приводит к заметному отклонению поведения реальных газов от идеального.

Основное уравнение молекулярно-кинетической теории идеального газа

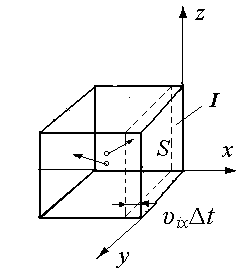
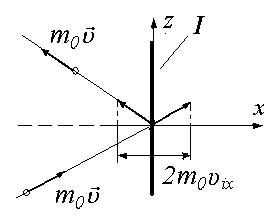
Рассмотрим объем газа в сосуде в виде куба (рис. 1.1, а) и определим давление на его стенку, например стенку I, перпендикулярную к оси x. В кинетической теории газов предполагается, что давление газа на стенку сосуда создается за счет упругих ударов молекул газа об эту стенку. Массы всех молекул считаются одинаковыми и равными m₀. При упругом ударе кинетическая энергия молекул сохраняется, и, следовательно, сохраняется, абсолютное значение скорости молекулы до и после ее удара о стенку. При упругом ударе под некоторым углом к поверхности стенки (см. рис. 1-1б) средняя сила, действующая на стенку вдоль оси z от соударений многих молекул, равна нулю. Поэтому передача импульса молекулы происходит только в направлении оси x (нормали к стенке). Проекция импульса на ось x изменяет свой знак (рис.1-1б).

Обозначим через n_i количество молекул в единице объема, проекции скорости которых на ось x равны ±υ_ix. Положительная проекция соответствует острому углу между вектором скорости и направлением оси, а отрицательная – тупому углу (см. рис.1-1б). При хаотическом движении количество молекул, имеющих положительные и отрицательные проекции на данную ось можно считать одинаковым и равным n_i /2, так как движение во всех направлениях равновероятно.

Из выделенной группы молекул за промежуток времени t стенки II с площадью S достигнут лишь те молекулы, скорости которых направлены к стенке, и которые находятся от стенки на расстоянии, не превышающем υ_ixt, или те молекулы, которые находятся внутри объема V = Sυ_ixt . Тогда полное число ударов молекул, содержащихся в объеме V, о стенку за время t равно:

. (1.11)

Если до удара молекулы о стенку проекция импульса на ось x была равна m₀υ_ix то после удара она станет равной (–m₀υ_ix)). Изменение импульса одной молекулы k_i при ударе молекулы о стенку равно импульсу, который передается стенке

k_i = m₀υ_ix –(– m₀υ_ix)) = 2 m₀υ_ix.

Рис.1.1

В результате ударов всех молекул, которые имеют проекцию скорости υ_ix, импульс, передаваемый стенке, будет равен

K_i = k_i N_ix= m₀υ_ix n_iSυ_ixΔt = m₀ n_iSυ_ix²Δt. (1.12)

Чтобы найти общее изменение импульса всех молекул при ударах о стенку К_х в направлении оси х, нужно просуммировать выражение (1.12) по всем значениям скоростей молекул, т.е. по всем υ_ix:

. (1.13)

Умножим и разделим правую часть (1.13) на концентрацию всех молекул в рассматриваемом объеме, которую обозначим через n:

. (1.14)

Величина в правой части есть среднее арифметическое, или просто среднее значение квадрата проекции скорости υ_ix, которое обозначим . С учетом (1.14 ) выражение (1.13) примет вид:

. (1.15)

Давление на стенку в направлении оси х будет равно:

. (1.16)

Так как по второму закону динамики F_x= ΔК_х/Δt, то согласно (1.16):

. (1.17)

По закону Паскаля p = p_x = p_y= p_z (p_y и p_z - давление на стенки, перпендикулярные осям y и z, соответственно). Записывая выражения аналогичные (1.17) для давлений p_y и p_z и складывая их, получим:

. (1.18)

Сумма средних квадратов проекций скоростей равна среднему квадрату полной скорости:

. (1.19)

Подставив (1.19) в равенство (1.18), получим:

,

откуда:

. (1.20)

Формула (1.20) определяет величину давления газа на стенки сосуда. Величину давления можно выразить через среднюю кинетическую энергию, приходящуюся на одну молекулу ε_k. Для этого умножим и разделим на 2 правую часть соотношения (1.20):

, (1.21)

где: . Формула (1.21) связывает давление газа со средней кинетической энергией молекул идеального газа. Эту формулу называют основным уравнением кинетической теории газов.

Пример 1-1. Оценка массы, средней энергии и скорости движения молекул в азоте при нормальных условиях.

Массу молекулы азота можно определить из соотношения (1.8):

При нормальном давлении p=10⁵ Н/м² в 1 м³ газа содержится n = = 2,7 · 10²⁵ молекул (число Лошмидта). Согласно формуле (1.21) средняя кинетическая энергия молекулы равна:

.

Скорость движения молекул можно оценить по формуле:

.

12