Лекция 13 введение в квантовую механику (продолжение)
13.1 Уравнение Шредингера для свободной частицы
При свободном
движении частицы ее потенциальная
энергия
= 0, а скорость движения постоянна
.
Направим ось х
вдоль вектора
,
а при соответствующем выборе начала
отсчета потенциальной энергии положим
U
= 0. Тогда стационарное уравнение
Шредингера (12.11) примет вид:
.
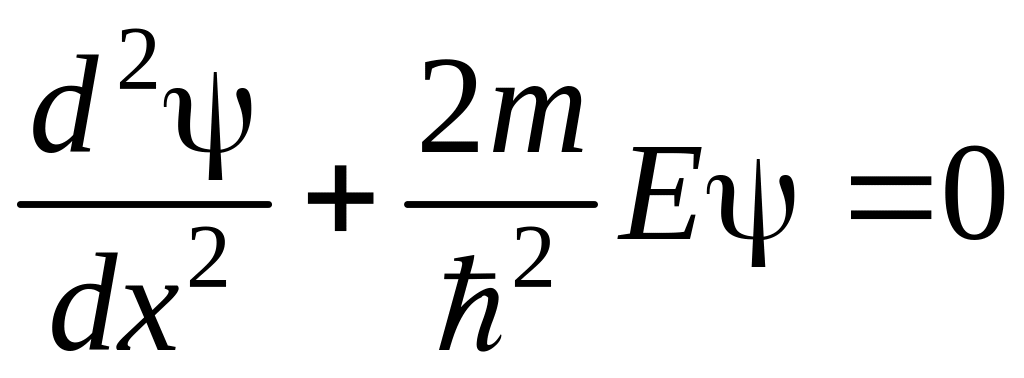(13.1)
Уравнение (13.1) имеет решение, которое представим в комплексном виде
,
где А и В – некоторые постоянные.
Решение нестационарного уравнения Шредингера в этом случае имеет вид:
.
(13.2)
Полученное
решение представляет собой суперпозицию
двух плоских монохроматических волн с
циклической частотой
,
одна из которых распространяется в
положительном направлении оси х
с амплитудой А,
другая
в противоположном направлении с
амплитудой В.
Из сопоставления с формулой (13.5) для
плоской монохроматической волны следует,
что волновое число k
для свободной частицы равно
.
Таким образом, свободной частице в квантовой механике сопоставляется плоская монохроматическая волна де Бройля.
13.2 Решение стационарного уравнения Шредингера для частицы в бесконечно глубокой прямоугольной потенциальной яме
Рассмотрим движение частицы вдоль направления х, при этом движение ограничено непроницаемыми для частицы стенками: х = 0 и х = l. Потенциальная энергия U в этом случае равна (рис.13.1):
U = 0 при 0 x l,
U = ∞ при x < 0 и x > l.
Уравнение Шредингера в этом случае имеет вид:
.
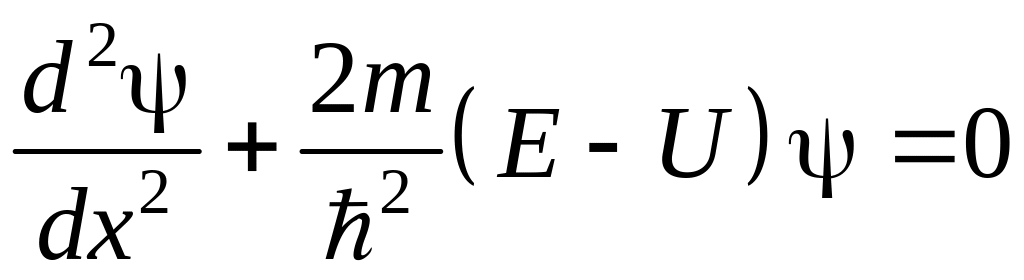(13.3)
Вероятность
обнаружить частицу за пределами ямы
равна нулю, так как частица не может
обладать бесконечно большой энергией.
Из условия непрерывности волновой
функции следует, что
должна быть равна нулю и на границах
ямы, т. е.
(13.4)
Рис. 13.1
В области, где не равна тождественна нулю, уравнение (13.3) принимает вид:
. (13.5)
Обозначим
,
тогда (13.5)
примет вид
.
Решение такого уравнения, как известно, имеет вид:
(x) = Asin(x + ).
Найдем и , используя граничные условия (13.4) Из условия (0) = 0 получаем:
(0) = Asin = 0,
откуда следует, что = 0. Из условия, что (l) = Asin l = 0 имеем:
l = n, (n = 1, 2, 3, …). (13.6)
Из соотношения (13.6) вытекает, что решение уравнения (13.5) будут иметь физический смысл не при всех значениях энергии Е, а только при значениях, удовлетворяющих условию:
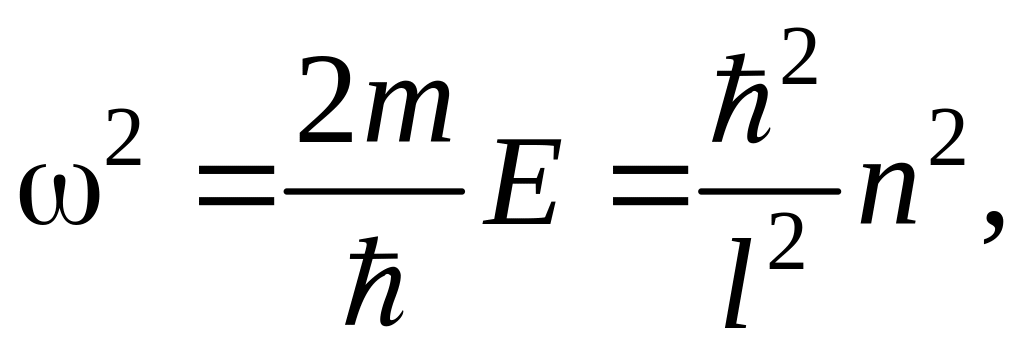(n
= 1, 2, 3, …)
откуда:
(n
= 1, 2, 3, …). (13.7)
Соотношение (13.7) указывает на то, что другие значения энергии частицы чем En невозможны: вероятность обнаружить внутри потенциальной ямы частицу с энергией, отличной от En , равна нулю. Физические величины, которые могут принимать лишь определенные дискретные значения, называются квантованными.
Таким образом, энергия частицы, находящейся в потенциальной яме, квантуется.
Квантованные значения Eп называются уровнями анергии, а числа п, определяющие энергетические уровни электрона, называются квантовыми числами.
Для определения коэффициента А воспользуемся условием нормировки волновой функции, которое в данном случае запишем:
.
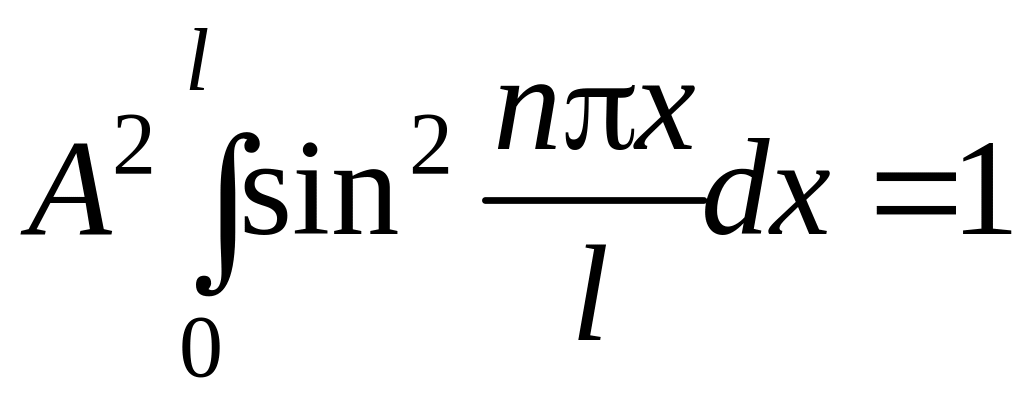Интеграл в последнем
выражении равен
.
В результате получим
,
откуда
.
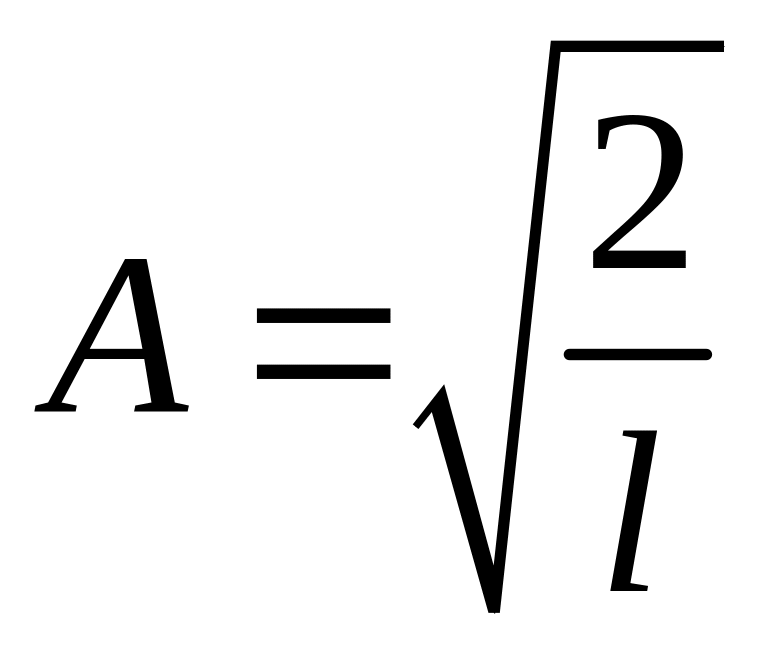Таким образом, собственная функция частицы в бесконечно глубокой потенциальной яме имеет вид:
.
(13.8)
Г
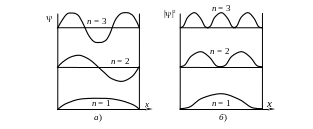рафики
плотности вероятности обнаружения
частицы на различных расстояниях от
стенки ямы при разных значениях n.
Рис. 12.3
Например, для потенциальной ямы с размерами, соизмеримыми с размерами атома величина l ~ 10–8 м, и собственные значения энергии электрона образуют последовательность энергетических уровней, расстояние между которыми ΔE = En+1 – En 1 эВ. В потенциальной яме макроскопических размеров ~1 см соседние энергетические уровни отличаются друг от друга на величину ~10–14 эВ.