1. Рівень держави :

• Вибір дослідницьких проектів

• Інвестиції інфраструктури

• Вибір політичних рішень

2. Рівень компаній, корпоративний рівень

• Вибір продукту

• Вибір ринку для цього продукту

• Вибір персоналу

• Вибір партнерів

• Вибір місця для виробництва

3. Рівень особистого життя:

• Вибір квартири

• Вибір університету

• Вибір автомобіля

• Вибір місця відпочинку

Типи шкал:

1. Кількісна шкала

2. Якість: якісна шкала (рівень, порядок, клас)

• Порядкова шкала

• Номінальна шкала

3. Шкала як частковий порядок (узагальнення)

Оцінювання складних систем може бути засноване :

1. Кількісна шкала

2. Порядкова шкала

3. Загальна шкала

ПРАВИЛО ПАРЕТО:

Зміст правила:

Альтернативи A=(A1, … , Ai , … , An) і критерії C=(C1, … , Cj , … , Ck),

Ai вектор оцінок zi = ( zi1 , …, zij , … zik )

Альтернатива X=(x1, … , xj , … , xk) і альтернатива Y=(y1, … , yj , … , yk),

X краще Y якщо  j xj  yj и  i (1 i  k) який xi > yi

A1, A3, A4 непорівнянні і не мають домінуючих елементів (Тільки Ao)

A1, A3, A4 є парето-ефективними рішеннями для безлічі

{A1, A2, A3, A4, A5}

Ролі в процесі прийняття рішень:

1. Особа, що приймає рішення (вибір кінцевого рішення, оцінка альтернативу)

2. Спеціаліст,організатор процедури прийняття рішення.

3. Експерт , що проводить оцінку різних альтернатив.

Контрольні запитання та завдання

1.Що потрібно для процесу вибору критерій властивостей?

2. Які існують підходи до проектування системи?

3. Розкажіть про принципи прийняття рішень?

4. Які прикладні проблеми прийняття рішень ?

5.Розкажіть зміст правила Парето?

Лекції 8 Основи побудови складних систем.

Процес математичного моделювання – вивчення явищ за допомогою математичних моделей.

Є 4 етапи цього процесу:

1) Етап синтезу моделі. На основі мети математичного моделювання, яку дослідник ставить перед собою, обирається математичний апарат, підхід до синтезу. Математичний апарат:

1. Детермінований (прямий опис);

2. Імовірнісний (описує статичні закономірності процесу);

3. Нечіткою логікою (на базі логіки)

Цей етап завершується записом у математичних термінах уявлень про зв’язки у об’єктному моделюванні.

2) Аналіз математичної моделі. На даному етапі за допомогою математичного апарату отримуються вихідні дані про моделі, які порівнюються з результатами здобутими експериментальним шляхом.

3) Перевірка адекватності синтезованої моделі – з’ясування того, чи відповідає побудована гіпотетична модель критерію практики (наскільки реальні результати відповідають теорії).

Якщо відхилення відходить за професійні межі, то така модель є неприйнятною. Кожен критерій має свою галузь застосування.

4) Ідентифікація моделі. Передбачає знаходження таких параметрів моделі, за яких її вихідна інформація є порівняною в межах точності спостережень з результатами спостережень явищ, які моделюються.

Приклад:

Гіпотеза 1.Кількість інформації «у», що зафіксувалася в пам’яті людини пов’язана з кількістю вхідної інформації «х».З логарифмічної функції у=lgx випливає, що зі збільшенням інформаційного потоку зростання вхідного потоку уповільнюється. Надмірна кількість інформації, що надходить немає сенсу.

Гіпотеза 2. Уявлення про предмет пізнання зв’язане з кількістю вхідної інформації про нього нелінійною функцією.

y=1-

y - уявлення про предмет пізнання;

b - поріг чутливості щодо інформації, яка надходить;

х – кількість вхідної інформації про предмет.

З цього співвідношення випливає, що пізнання про предмет монотонно зростає зі зростанням х, наближаючись до 1.

Особливими точками першої і другої функції є точка (1;0), де ці функції =0. Це означає, що один неізольований факт не несе інформації про уявлення про предмет.

Два факти про предмет до формули (1) дадуть рівень пізнання у=0,5, точка х=7,3 є коренем такої системи: y=lgx

y=1-

і свідчить про достатню повноту вхідної інформації.

Якщо ми в колективі, де є не більше 8-ми людей, тов. такому колективі ще можливе утримання єдності інтересів.

Гіпотези можуть бути використані під час синтезу моделей системи для оцінки повноти та інформації про систему, що закладається у модель, яка синтезується.

ЦС

БС

БС

АС

АС

АС

АС

АС

АС

Рис. 8.1 Ієрархічна модель системи зв’язку

ЦС – центральна станція

БС – базова станція

АС – абонентська станція

- паразитні зв’язки (перехресні завади)

Горизонтальні зв’язки на даному рівні це паразитні зв’язки.

Обмежуючись розглядом задачі електромагнітної сумісності, можна вважати, що крім вертикальних звязків, які визначають організацію зв’язку і керування існують також горизонтальні та перехресні зв’язки, які не передбачаються схемою організації зв’язку, хоча вносять характерну для електромагнітної сумісності специфіку в процес функціонування системи зв’язку в цілому.

Оптимізація ієрархічних систем управління

Слід зазначити, що найбільш поширеною формою побудови складних систем управління є ієрархічна побудова. Системи ієрархічної структури є компромісним варіантом між системами з винятково централізованою чи децентралізованою конфігурацією, що забезпечує їм поліпшені показники оперативності, надійності, живучості та стійкості управління в цілому. Що стосується систем мережного управління, які побудовані у відповідності до вже згадуваних технологій TMN та TINA, то вони також мають чітко визначену ієрархічну побудову відповідно з чотири та трирівневою структурою.

Методи оптимізації ієрархічних систем управління

1.Метод цільової координації;

2.Метод прогнозування взаємодій,

які забезпечують оптимізацію ієрархічних систем управління, представлених лінійними моделями з квадратичним критерієм якості. В декомпозиційному представленні диференційна модель (9.42) трансформується в систему рівнянь

, (8.1.1)

що визначають динаміку -ї підсистеми .

Варто окремо зазначити, що в залежності від особливостей побудови системи, що моделюється, декомпозиція може відбуватися як за змінними стану, так і за змінними управління. Тоді у першому випадку має місце співвідношення

, (8.1.2)

а в іншому випадку

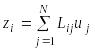.(1.3)

Акцентуючи свою увагу в подальшому лише на першому випадку, критеріальна функція (9.43) приймає вигляд

.(8.1.4)

Метод цільової координації

Метод цільової координації [2] базується на можливості перетворення вихідної задачі мінімізації в більш просту задачу максимізації і розв’язання цієї задачі з використанням дворівневої ітеративної обчислювальної процедури. Для цього визначимо двоїсту функцію наступним чином:

(8.1.5)

при

, (8.1.6)

де - вектор множників Лагранжа; - лагранжіан, створений введенням умови (1.3). Теорема щодо строгої дуальності задач на умовний екстремум дозволяє стверджувати, що для задач з лінійними обмеженнями та квадратичною критеріальною функцією має місце рівність

, (8.1.7)

тобто розв’язання задачі мінімізації виразу (10.9) у відповідності з обмеженнями, що задані лінійними рівняннями (10.7) та (10.8), еквівалентно розв’язанню задачі максимізації двоїстої функції .

Рівняння (1.6) для заданих перетвориться до вигляду

.

Таким чином, лагранжіан приймає адитивну форму та може бути представлений в декомпозиційному вигляді з доданків – незалежних підлагранжианів для кожної з підсистем. Тобто, для раніш заданих , необхідно мінімізувати підлагранжіани

(8.1.8)

незалежно для кожної з підсистем, для якої існує підсистема динамічних обмежень (1.2). Отримані рішення визначають можливість у відповідності до рівняння (1.7) обчислювати значення функції , яке потім можна ефективно поліпшувати завдяки ітеративного обміну інформацією з другим рівнем, де коректується значення , використовуючи рішення незалежних задач мінімізації (1.8) на першому рівні. При формалізації процедури мінімізації величини використовувалася та обставина, що можливо знайти досить порості вирази для градієнта функції , розглядаючи як аргументи рішення задач мінімізації першого рівня. Фактично градієнт визначається помилками в обчислених характеристиках взаємодії підсистем, тобто

. (8.1.9)

Таким чином, для розв’язання задачі можна визначити дворівневий ієрархічний алгоритм, де на першому рівні для заданих значень , отриманих на другому рівні, мінімізуються підлагранжіани у відповідності з динамічними обмеженнями. Результуючі значення векторів та направляються на другий рівень, на якому ці вектори співставляються у відповідності до рівняння (8.1.10) для формування вектора похибок взаємодії, що, в свою чергу, використовується в градієнтній процедурі для отримання нових значень . Наприклад, для переходу від -ї ітерації до -ї необхідно знайти

, (8.1.10)

де - довжина кроку, а - напрямок руху, обраний у відповідності до координат градієнта . Загальний оптимум досягається коли стає близьким до нуля.

У рамках методу цільової координації помітно полегшений облік обмежень на змінні стану і управління при розв’язанні задач нижнього рівня. Оперативність розв’язання задач нижнього рівня багато в чому визначається швидкістю збіжності градієнтних процедур (8.1.10).

При реалізації методу цільової координації значно спрощуються функції управляючих систем верхнього рівня, але помітно ускладнюється робота систем нижнього рівня. Метод орієнтований винятково на використання в багатофазних координуючих процедурах, тому що реалізується тільки по закінченні процесу координації. Введення доданка у виразі (8.1.3) виправдується у випадку можливості отримання аналітичного розв’язання задачі для запобігання вироджених рішень. У інших випадках цей доданок з критеріальної функції (8.1.3) можна вилучити.

Метод прогнозування взаємодій

В рамках методу прогнозування взаємодій необхідно мінімізувати функціонал

, (8.10.16)

у якому відсутні квадратичні вирази відносно .

Запишемо лагранжіан у вигляді

, (8.10.17)

де - вектор множників Лагранжа. Якщо задатися значеннями та , то вираз (11) дістає вигляду

, (8.10.18)

де

. (8.10.19)

На відміну від методу цільової координації як координуючий виступає вектор , розмірність якого дещо зросла. Однак алгоритм другого рівня виявляється надзвичайно простим, що гарантує відсутність додаткових складнощів, пов’язаннях з ростом розмірності координуючого вектору.

Алгоритм координатора другого рівня поліпшує компоненти координуючого вектору з використанням значень вектору попередньої ітерації, тобто

,

де вирази правої частини отримуються шляхом виконання умов

та ,

при цьому і , що призводить, в кінцевому випадку, до наступного координаційного алгоритму:

. (8.10.20)

Таким чином, в основу методу прогнозування взаємодій покладено мінімізацію незалежних підлагранжіанів (10.19) для заданих значень та , а отримані в результаті розв’язання цих задач оптимальні значення векторів та використовуються для обчислення нових оцінок величин та у відповідності до рівняння (10.20).

Дієвість методу прогнозування взаємодій залежить від точності прогнозування сигналів взаємодії або, у більш широкому змісті, - від впливу помилок прогнозування. Швидкість збіжності координаційних процедур також залежить від точності прогнозування величин сигналів взаємодії. У загальному випадку при реалізації даного методу в порівнянні з методом цільової координації дещо ускладнюється робота координаторів верхнього рівня, але спрощуються задачі нижнього рівня. У разі можливості аналітичного розв’язання оптимізаційної задачі функції координатора верхнього рівня значно спрощуються і використовувати градієнтні процедури непотрібно.

До переваг методу прогнозування взаємодій варто віднести можливість використовувати координаційні сигнали на будь-якому кроці координаційної процедури, що дозволяє реалізувати "лінійну" або секвенційну координацію, помітно знижуючи, тим самим, обсяг переданої службової інформації.

Теоретико-ігрові моделі задачі каналів функціонування системи зв’язку

У взаємодії динамічних систем Si можливі такі характерні стратегії поведінки:

1) Антагоністична, коли учасники мають протилежні інтереси, протилежні стратегії і гра учасників зводиться до створення двох коаліцій.

Для моделювання електромагнітних взаємодій, в тому числі для забезпечення електромагнітної сумісності, така модель не є конструктивною, вона характерна для радіо-електронної боротьби.

2) Стратегія байдужості або гра з природою, коли стратегія j-го гравця не залежить від стратегії i-го гравця.

3) Кооперативна стратегія, коли у всіх гравців є загальна мета та їхні стратегії утворюють єдиний вектор.

Очевидно, що для аналізу систем найбільш придатними є дві останні стратегії.

Для побудови моделей необхідно застовосувати досить складний апарат марківських ланцюгів, які описуються за допомогою рівняння.