
- •4.Зад.О.Диете
- •8. Геом интерпр-ия задачи лп с несколькими переменными.
- •9.Формы записи задачи лп
- •10.Переход к канон.Ф.:
- •13.Основная теорема лп
- •14) Построение начальнопорн плана
- •20.Двойст и прям зад-ча
- •21.Теория двойст. Эк сдерж
- •22. Критерий оптим-ти Канторовича
- •23. Малая теор.Двойств.
- •27. Постановка тз по критерию стоимости.
- •28.Трансп-ная табл. Теорема о сущ-нии допуст плана.
- •30. Правило «северо-западного угла»
- •30.Прав «миним эл-та» (наим стоим»)
- •31. Теор о потенц. Алг теор
- •31.Циклы и их использ
- •33.Тз с макс-ей цф
- •34.Пост-ка и мат.Модель задачи цп.
- •35. Реш зад цп мет отсеч
- •39.Метод ветвей и границ.
- •40. Понят о дп.Особен.
- •41. Понятие о дп. Геом. Интерпр.
- •47. Задача замены оборуд
- •49.Метод множ-лей Лагр-жа реш-я задачНп.Экон-й смысл множ-ей Лагр-жа
- •50.Градиент.Метод решения задачНп
1.Мат. Прогр-е – область прикладной математики, разраб-щая теорию и численные методы решения многомерных, экстрем-х задач с ограничением, т.е. задач на экстремум ф-ции многих переменных с ограничением на область измен-я этих переменных. ЭММ –система мат. Ф-ций, уравнений, неравенств, описывающих реал-й эконом-й объект, сставляющие его характ-ки и взаимосвязи м-ду ними. Модель задачи МП можно записать в виде: max (min)F = f(x1,x2,…xn), (1); ϕi (x1,x2,…xn) { ≤, =, ≥} bi, i=1,m. (2); xj ≥ 0, j =1,n. (3) . 1 – ЦФ-показатель эффективности, критерий оптимальности. В качестве ЦФ мб прибыль, объем выпуска или реализации, отходы и т.д.; 2 – основные;3 – прямые ограничения. Матем-ки ограничения запис-ся в виде уравн-й и нерав-в, сов-ть которых образ-т ОДР. Сов-ть независимых величин Х=( x1,x2,…xn), действуя на которые систему можно совнршенств-ть, наз. планом задач. План Х, удовлетворяющий основным и прямым ограничениям наз-ся допустимым. Допустимый план, доставл-щий ЦФ экстрем. значение наз. оптимальным и обознач-ся Х*. Аналогично экстр. Значение ЦФ обознач-ся F*=F(X*). В завис-ти от свойств ф-ций f и ϕi (i=1,m) МП можно рассматривать как ряд самост. величин. Задачи МП делятся на задачи линейного и нелинейного прогр-я. Среди задач нелин. пр-я наиболее глубоко изучены задачи выпуклого программ-я, в рез-те реш-я которых опред-ся min выпуклой (max вогнутой) ф-ции, заданной на выпуклом замкнутом множ-ве. Отдел-ми класс-ми задач явл. задачи целочисл-го, параметрич-го, дробнолин-го прогр-я. В з-х целоч. прогр-я на искомые перемен-е налаг-ся усл-е целочисл-ти, а ОДР конечное. В з-х парам. прог-я ЦФ или ф-ции, опред-щие ОДР либо то и другое зависят от некоторого параметра. В з-х дробнолин-го пр-я ЦФ предст-т собой отнош-е 2-х лин-х ф-ций. Выдел-т также з-чи стохастического и динам-го прогр-я. В з-х дин-го пр-я процесс нахождения реш-я явл-ся многошаговым. В з-х стохаст-го пр-я в ЦФ или в ф-ях из ОДР содерж-ся случ-е величины.
2.Задачи МП деляться на линейного и нелин-го программ-я. Выд-т задачи: целочисленного,параметрического, дробно-линейногопрог-я. Парамет-го прог-е ЦФ и ф-ции опред-щие ОДР зависят от некот-х параметров. В задачах др-линейного пр-я Цф пред-т собой отношение 2-х линейн-х ф-ции. Выд-т задачи: стохостического, динамического пр-я. В задачах динамин-го пр-я процесс нахождения решения явл. многошаговым.
3.ЛП – раздел МП, в котором разраб-ся методы нахождения экстр-ма лин-х ф-ций при лин-х дополн-х огранич-ях, налаг-мых на эти перемен-е.
зад.о.наилуч.исп.рес-в
n-прод-и; m-рес-сы; cj,j=1,n – цена ед-цы прод. j-го вида; bi,i=1,m – кол-во i-го рес-са; aij, j=1,n, i=1,m – кол. i-го рес-са, необход. для пр-ва прод-и j-го вида.Треб-ся опр-ть план пр-ва кажд.прод-и X*=(x1*,x2*…xn*), при кот. обесп-ся max-ая выручка.
Цена общего V реал-ии:F=c1x1+c2x2+…+cnxn.
Расход на пр-во всех n видов прод-и не должен превышать bi: ai1x1+ai2x2+…+ainxn≤bi, i=1,m.
Усл-е неотриц-ти:xj≥0, j=1,n.
ЭММ:maxF=

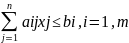
xj≥0
4.Зад.О.Диете
n - кол-во прод-ов питания;m – питат-е вещ-ва; cj,j=1,n – цена ед-цы прод-та; bi,i=1,m – min-е кол-во i-го полезного вещ-ва; aij, j=1,n, i=1,m –содерж-е i-го вещ-ва в ед-це j-го прод-та.Треб-ся опр-ть кол-во приобретения кажд. вида прод. X*=(x1*,x2*…xn*),обесп-е необх.кол-во полез.вещ-в при min-ой общей стоим-ти прод-в питания.
ЭММ:minF=
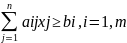
xj≥0
5.Задача о выборе оптимальных технологий. В задаче о наилуч использ рес-ов опред-ся оптим-ый план выпуска продукции. Пусть при произ-ве какого-то общественно необход продукта использ-ся n технологий. При этом треб-ся т видов рес-ов, заданных объемами bi (i = 1, m). Эффек-ти технологий, т. е. кол-во конечной продукции (в ден. ед.), производ в ед. времени по j-й (j= 1,n) технологии, обозначим cj. Пусть, далее, аij- — расход i-го ресурса в единицу времени по j-й технологии. В качестве неизвестной величины xj примем интенсивность использ j-й технологии, т. е. время, в течение которого продукция произв-ся по j-й технологии. Пренебрегая временем переналадок, необход для перехода от одной технологии к другой, получаем следующую математическую модель задачи: найти план интенсивностей использования технологий х = (xi;... ;хn), обеспеч-ий макс выпуска прод в стоим-ом выраж: ∑aijxj≤bi (i=1,m) при огранич -ях на лимит-е ресурсы: max Z= ∑cjxj и условии неотрицательности: xj≥0 (j=1,n).
6.Задача о раскрое материалов. Суть задачи об оптим-ом раскрое состоит в разраб-ке таких техн-ски допуст планов раскроя, при кот получ-ся необход комплект заготовок, а отходы (по длине, площади, объему, массе или стоимости) свод к минимуму. Рассмотрим простейшую модель раскроя по одному измерению. Более сложные постановки ведут к задачам целочисл программ-ия. Модель задачи раскроя по одному измер длинномерных материалов (прутков, труб, профильного проката и др.) может быть сформул так. Пусть имеется N штук исходного материала, длина каждой штуки равна L. Нужны заготовки т видов, длины которых равны Li (i = 1,n). Известна потреб-сть в заготовках каждого вида, она равна b{. Изучение вопроса раскроя (построение технол-ой карты раскроя) показ-ет, что можно выделить n приемлемых вариантов раскроя исход матер длиной L на заготовки длиной Zj. Обозначим через aij количество заготовок i-го вида, получаемое при раскрое единицы исходного материала по j-му (j=1,n) варианту, Cj — отходы при раскрое единицы исходн матер по j-му варианту. План задачи х = (х1;... ; xj ... ;хn), где xj — количество единиц исходного материала, планируемое к раскрою по j-му варианту.Функция цели — мин отходов, получ при раскрое: min Z = ∑cjxj при огранич: на число ед исх матер: ∑xj≤N
8. Геом интерпр-ия задачи лп с несколькими переменными.
Перейдем к геометрической интерпретации ЗЛП с несколькими переменными.
max F = , (1)
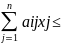 bi,
(i=
bi,
(i=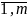 ),
(2)
),
(2)
xj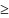 0,
(j=
0,
(j=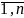 ).
(3)
).
(3)
Множ-во
реш Х = (х1,х2,…,хn),
компоненты кот удовл-ют огранич-ю-
равенству ai1x1
+ ai2x2
+… + ainxin
= bi,
(i=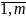 ),
геом-ски пред-ют собой гиперплоскость
n-мерного
пространства. Это выпуклое множ-во.
),
геом-ски пред-ют собой гиперплоскость
n-мерного
пространства. Это выпуклое множ-во.
Множ-во
реш Х = (х1,х2,…,хn),
ком-ты кот удовл-ют нер-ву ai1x1
+ ai2x2
+… + ainxin bi,
(i=
),образ
полупрос-во n-мерного
простр-ва, кот также явл выпуклым
множ-вом.
bi,
(i=
),образ
полупрос-во n-мерного
простр-ва, кот также явл выпуклым
множ-вом.
Множ-во
реш, удовл-их системе огранич задачи
ЛП (2), (3) предст собой пересечение
конечного числа полупространств и
поэтому явл выпуклым. Теорема:Множ-во
реш ЗЛП выпукло (если оно не пусто).
Множ-во реш задачи ЛП в практически
важных случаях чаще всего предст-ет
собой либо выпуклый многогранник, либо
выпуклую многогранную область. ЦФ (1)
геом-ки можно рассм как семейство паралл
гиперплоскостей с1x1
+ с2x2
+… + сnxn
=F,
каждой из кот соот-ет опред знач параметра
F.
Вектор
 = (с1;
с2;
…;сn),
перпенд-ый к гиперплоскости F=const,
указ направл наискорейшего возраст
функции F.
С учетом сказ задача (1)-(3) геом-ки свод.
к нахождению точки Х*
= (х1*,х2*,…,хn*)
многогранника, опред нерав-ми (2), (3),
через кот проход гиперплоскость
семейства (1), соот-щая наиб знач F.
Граф методом можно решить ЗЛП с n>2
перем, если в ее канон-ой записи число
неизв n
и число линейно-независ векторов m
связ соотнош-ем n-m
2.
= (с1;
с2;
…;сn),
перпенд-ый к гиперплоскости F=const,
указ направл наискорейшего возраст
функции F.
С учетом сказ задача (1)-(3) геом-ки свод.
к нахождению точки Х*
= (х1*,х2*,…,хn*)
многогранника, опред нерав-ми (2), (3),
через кот проход гиперплоскость
семейства (1), соот-щая наиб знач F.
Граф методом можно решить ЗЛП с n>2
перем, если в ее канон-ой записи число
неизв n
и число линейно-независ векторов m
связ соотнош-ем n-m
2.
