2.2 Векторне вираження кольору

Тривимірність кольору дає основу виразити його у вигляді вектору в просторі.

У системі прямокутних координат (рис. 2.1) координатні осі символами основних кольорів (RGB). Колір К заданий рівнянням:

(2.1)

Відповідно до рівняння можна відкласти вектор К. Його проекції на координатні осі колірні, що становить 4R, 3G, 2В.

Використовуючи координатні осі, можна знайти вектори будь-якого кольору, що утворюється за допомогою вибраних основних. Сукупність кольорів, виражена в цій системі основних, називається колірним простором системи. Кожній точці цього простору відповідає певний колір, тому що будь-яку точку можна розглядати як кінець вектору, проведеного з початку координат.

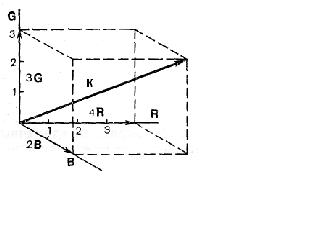
Рис. 2.1 – Вектор кольору, що описується рівнянням (2.1), у просторі RGB

Відповідно до третього закону Грассмана колірні рівняння, адитивні: якщо складаються два кольори, то сумарний має колірні координати, що дорівнюють сумі координат кольорів, що складаються. Вектор сумарного кольору дорівнює сумі векторів і може бути розрахований за правилом паралелограма.

У колірному просторі вектор кольору має певний напрям. Він виходить адитивним складанням основних кольорів. Якщо блакитний не насичений, то його вектор відхилений від площини на той або інший кут.

Дуже важливе питання про зміну насиченості та яскравості в колірному просторі. Оскільки ахроматичні кольори мають рівні колірні координати, то усі вони знаходяться в колірному просторі на лінії, рівновіддаленій від координатних осей. Ця лінія (ЧБ на рис. 2.2) називається ахроматичною віссю. Чим більші чисельні значення мають колірні координати, тим більше яскравості кольорів. Точці М ахроматичної осі відповідає мала яскравість (темно-сірий колір), а точці N – велика (світло-сірий). На початку координат лежить точка Ч нульової яскравості, що виражає чорний колір. Точка Б визначає положення білого кольору в колірному просторі.

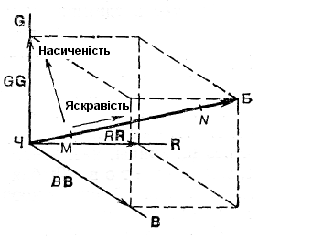
Рис. 2.2 – Схема залежності характеристик кольору від його положення в колірному просторі

Якщо колірні координати мало відрізняються один від одного, то колір, знаходиться поблизу ахроматичної осі. Отже, насиченість кольору в колірному просторі зростає за мірою віддалення від ахроматичної осі. Зміна насиченості та яскравості показана стрілками.

Колірний простір має деякі специфічні властивості. Так, до нього незастосовне поняття відстані, кута; в той же час можна говорити про відношення довжин і кутів.

2.3 Особливі площини та лінії колірного простору: площина одиничних кольорів, площина рівних яскравостей, лінії рівних яскравостей, аліхна

Площина одиничних кольорів. Як відомо, B_R = 1, якщо яскравість кольору R = 680 кд∙м^–2; В_G = 1 при В = 3121 кд∙м^–2 і B_В = 1 при В = 41 кд м^–2. Отже, ОВ_R, ОВ_G, ОВ_В (рис. 2.3) – одиничні відрізки. Площина Р, що проходить через їх кінці, називається площиною одиничних кольорів. Будь-яка її точка виражає одиничний колір, тобто такий, сума координат якого (тобто модуль кольору) дорівнює одиниці.

З аналітичної геометрії відоме рівняння площини у відрізках:

(2.2)

де х, у, z – поточні координати; а, b, с – відрізки, що відсікаються площиною на координатних осях.

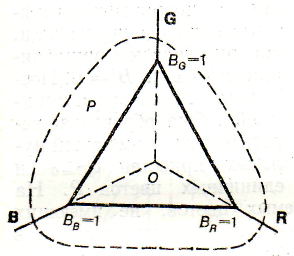
Рис. 2.3 – Площина одиничних кольорів і трикутник колірності

Таким чином рівняння (2.2) має вигляд:

(2.2,a)

За побудовою В_R = В_G = В_B=1. Тому r + g + b = 1.

Отже, сума колірних координат (модуль) кольору, заданого будь-якою точкою площини Р, дорівнює одиниці, тобто Р, що і треба довести, є площина одиничних кольорів, або, що те ж, площина колірності. Яскравість будь-якого кольору, що лежить в ній, дорівнює яскравісній колориметричній одиниці, що виражається різним числом кд∙м^–2 залежно від значення колірних координат.

Трикутник, утворений перетином площини одиничних кольорів з координатними площинами (рис. 2.3), називається трикутником колірності або колірним трикутником.

Площини рівних яркостей. Кольори, що лежать на площині одиничних кольорів, мають однакові яскравості, виразимо в колориметричних одиницях, але різні – в кд∙м^–2. Визначимо тепер положення геометричного місця точок, що відповідають постійним значенням яскравостей в кд∙м^-2.

Відкладемо на координатних осях RGВ (рис. 2.4) точки S, T і U, що мають яскравості, рівні 680 кд∙м^–2. Масштаб по координатних осях виберемо в яскравісних колориметричних одиницях В_R, В_G, В_B. Отже, для того, щоб відкласти задані точки, треба виразити яскравість 680 кд∙м^–2 в значеннях яскравісних колориметричних одиниць. 680 кд∙м^–2 складають одну яскравісну одиницю В_R, 0,22 одиниць В_G і 17 одиниць В_B.

Проведемо через точки S, Т і U площину Q₁, що називається площиною рівних яскравостей. Кожна її точка в нашому прикладі виражає колір, яскравість якого дорівнює 680 кд∙м^–2. Це можна довести, прийнявши 680 кд∙м^–2 за одиницю яскравості і застосувавши формулу (2.2).

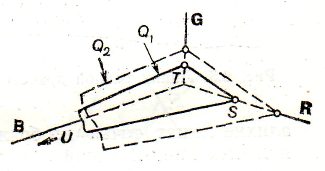
Рис. 2.4 – Площини рівних яскравостей

Якщо відкласти на осях координат не 680, а, наприклад, 1360 кд∙м^–2 і провести через відкладені точки площину Q₂ виявиться паралельною Q_1. Отже, в колірному просторі RGВ (як і у будь-якому колірному просторі) знаходиться ряд взаємно паралельних площин рівної яскравості. Можна уявити собі площину нульових яскравостей Q_0. Вона паралельна Q₁ і Q₂ і проходить через початок координат. У ній лежать точки безяскравісних кольорів. Такі кольори, звичайно, бачити не можна, але уявити можна. Ще нижче розташовані площини також уявних кольорів, що мають негативні яскравості. Площина нульової яскравості має в колориметрії важливе значення.

Лінії рівної яскравості. Лінії перетину площини одиничних кольорів з площинами рівної яскравості називаються лініями рівної яскравості. На рис. 2.5 показані лінії В = 1 і В = 0. Остання називається аліхною. Вона утворена перетином площин нульових яркостей Q_B = 0 і одиничних кольорів. На аліхні лежать точки уявних кольорів, що не мають яскравості.

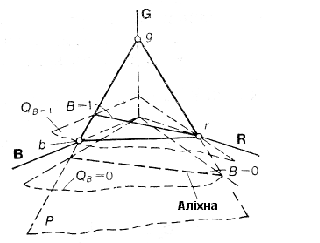
Рис. 2.5 – Лінії рівної яскравості

Положення аліхни на діаграмі. Оскільки колір є тривимірною величиною, він може бути представлений вектором в тривимірному просторі, який називають колірним. При цьому довжина вектору характеризує кількість кольору, а напрям вектору його якість – колірність. Усі вектори в колірному просторі виходять з точки нульової яскравості, що відповідає чорному кольору (адже при зменшенні яскравості будь-якого кольору до нуля він сприймається як чорний). Колірний простір займає менше півсфери, оскільки не існують колірні вектори протилежних напрямів (інакше при підсумовуванні кольорів, що представляються ними, можна було б отримати чорний колір). Згідно з другим законом, усі кольори примикають один до одного, отже, окремо віддаленого колірного вектору в колірному просторі бути не може (рис. 2.6).

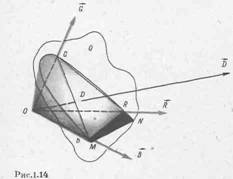
Рис. 2.6 – Положення аліхни на діаграмі

Якщо на одну грань матової скляної призми направити світловий потік, що вивчається, наприклад Е, а на іншу її грань – потоки трьох основних кольорів R, G, В (рис. 2.7), то можна так підібрати інтенсивності основних кольорів, що глядач, спостерігаючи одночасно кольори на обох гранях призми, оцінить їх як однакові (погоджені) по яскравості і колірності. Процес досягнення цієї умови називається узгодженням кольорів. У такий спосіб експериментально встановлено, що для отримання білого рівно-енергетичного випромінювання Е яскравісні коефіцієнти L΄_R, L΄_G, L΄_B одиничних кількостей основних кольорів повинні задовольняти співвідношенню L΄_R : L΄_G : L΄_B : = 1:4, 59:0,06.

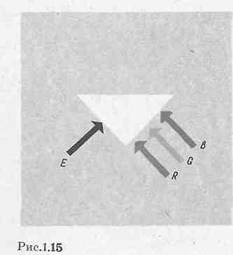
Рис. 2.7 – Потоки трьох основних кольорів

Яскравісний коефіцієнт L΄ і яскравість L, виражена в кд/м², пов'язані простою залежністю L =683L’.

Отже, одиничні кількості кольорів R, G, В мають яскравості:

(2.3)

Якщо відомі яскравісні коефіцієнти для основних кольорів, значить, визначені яскравісні масштаби по координатних осях, і тоді яскравісний коефіцієнт L΄ будь-якого кольору F може бути виражений через модулі основних кольорів:

(2.4)

Це рівняння площини. Отже, кольори рівної яскравості в колірному просторі лежать в одній площині, званій рівнояскравою. Усі рівнояскраві площини паралельні між собою. Поклавши L΄F =0 отримаємо рівняння площини MON (рис. 2.6) нульової яскравості. Лінія MN перетину цієї площини з одиничною площиною Q називається аліхною, тобто безколірною. Прирівнявши нулю яскравісне рівняння для площини Q маємо:

Підставивши значення яскравісних коефіцієнтів основних кольорів, знайдемо рівняння аліхни в площині Q :

Криві складання, знайдені Гилдом і Райтом, також як і криві, отримані Максвеллом, мають недоліки, і для більшості кольорів спектру, за винятком трьох основних кольорів (R = 700 нм, G = 546.1 нм і В = 435,8 нм), перекриваються.