1.4 Основи колориметричної системи xyz [1-3]
Колір Ц в системі RGB являє собою суму основних помножених на координати кольору: Ц = rR + gG + bB. Одночасно з цією системою була прийнята інша система – XYZ, основні кольори якої вибрані більш насиченими. Система XYZ дозволяє спростити розрахунок кольорових координат і яскравостей.
З рис. 1.4 видно, що негативні координати можна вилучити, якщо в якості основних кольорів замість R, G і B використовувати інші кольори – X, Y і Z, які повинні бути обрані так, щоб вся область реальних кольорів, зокрема і основні R, G і B, вписувались в трикутник XYZ. Очевидно, що самі ці кольори реально не існують, тобто їх точки знаходяться за межами лінії спектральних кольорів.
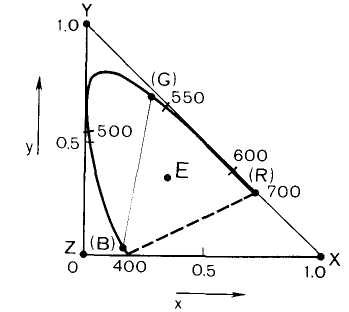
Рис. 1.4 – Кольоровий трикутник XYZ
Таким чином, колірності нових основних кольорів X, Y і Z були вибрані з умов виключення негативних координат. Нам відомо, що основні кольори повинні бути визначені також за відносними яскравостями, тобто повинні бути визначені одиничні кольори. Для спрощення розрахунків прийнято, що яскравості двох основних кольорів – X і Z – дорівнюють нулю. Тоді яскравості кольорів, що отримані змішуванням X, Y і Z, будуть збігатися з яскравістю кольору Y. Фізично не можна отримати і навіть уявити собі кольори з нульовою яскравістю, але в колориметричних розрахунках ми цілковито вільно можемо відокремити яскравість кольору від його колірності, тобто ці характеристики незалежні один від одного.
Як і в системі RGB, суміш рівних кількостей кольорів X, Y і Z дає білий колір з колірністю Е, точка якого лежить в центрі трикутника XYZ. Лінія спектральних кольорів і, отже, всі точки реальних кольорів лежать всередині трикутника XYZ. Кольори R, G і В є спектральними. Тому точки їх колірностей можна знайти на лінії спектральних кольорів. Але в трикутнику XYZ кольори, які співпадають за колірностями з кольорами R, G і В, не співпадають з ними за відносними яскравостями. Це пояснюється тим, що кольори з колірностями R, G і В, що утворюються змішуванням кольорів X, Y і Z, мають відносні яскравості, які не співпадають з яскравостями одиничних кольорів R, G і В. Тому на графіку XYZ вони, на відміну від R, G і В, позначаються (R), (G) і (В).
Очевидно, що колориметричні досліди нереальними кольорами виконати не можна. Система XYZ розрахована за системою RGB і, отже, заснована на тих же колориметричних дослідах з реальними кольорами, на яких заснована система RGB. Співвідношення між кольорами X, Y і Z і кольорами R, G і B виражаються наступною системою рівнянь:
(1.8)
За рівнянням (1.11) можна визначити залежність між координатами кольорів в системах XYZ і RGB, яка має наступний вигляд:
(1.9)
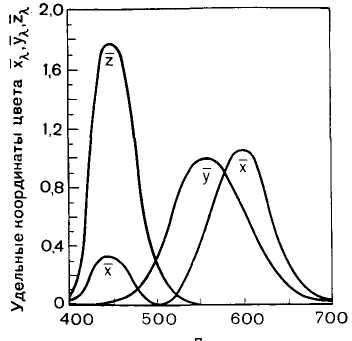
За рівнянням (1.11) можна також визначити питомі координати x, у і z, підставивши в них відомі величини r, g і b. Графіки залежності x, у і z від (криві змішування кольорів) наведені на рис. 1.5. Величини питомої координати у дорівнюють видностям V. Тому яскравість кольору в системі XYZ визначається величиною координати у'. Якщо визначається колір випромінювання, що відображається або проходить через якийсь освітлений зразок, то координата у' чисельно співпадає з коефіцієнтом відображення або пропускання цього зразка. Яскравість кольору визначається за формулою:
(1.10)
Таким чином, в міжнародній колориметричній системі XYZ основними є неіснуючі реально кольори X, Y і Z, які розраховані як математичні комбінації реальних кольорів R, G і В. Колірності і яскравості кольорів X, Y і Z вибрані так, щоб спростити розрахунок координат кольорів і їх яскравостей. Всі закономірності додавання кольорів, вираження кольорового тону і чистоти кольору, які ми розглядали в системі RGB, що застосовуються також і до системи XYZ. Техніка розрахунку координат кольорів х', у' і z' за питомими координатами х, у і z і спектральними складами випромінювань така ж, як в системі RGB.
Питомі координати кольору х, у, z |
|
Рис. 1.5 – Залежність питомих координат кольору від довжини хвилі у системі XYZ