2.10 Вираження колірності в системі xyz

Вимоги до основних кольорів XYZ. Практично використовуваною колориметричною системою є ХУ.

Основні кольори ХУ обрані для максимального спрощення колірних розрахунків і вимірів. Вибір був зроблений таким чином, щоб забезпечити наступні властивості системи:

1. Яркістна характеристика кольору визначається не трьома складовими колірного рівняння, а тільки однією.

2. Колірне рівняння, що виражає будь-який реальний колір, включаючи найбільш насичені – спектральні, не мають негативних координат.

3. При зазначених особливостях системи положення білої точки зберігається в центрі трикутника кольоровості та координати білого кольору є Б (1/3; 1/3; 1/3).

4. Одна з колірних координат великого числа спектральних кольорів дорівнює нулю, і ці кольори, отже, виражаються двочленними рівняннями.

Ці властивості пов'язані з особливостями будови колірного простору ХУ.

Нереальні кольори. За межами площі, обмеженої локусом, розташовуються точки кольорів, яких немає в природі, – більш насичених, ніж спектральні. Виберемо поза полем реальних кольорів точку Бл (рис. 2.19) і охарактеризуємо колір, виразом:

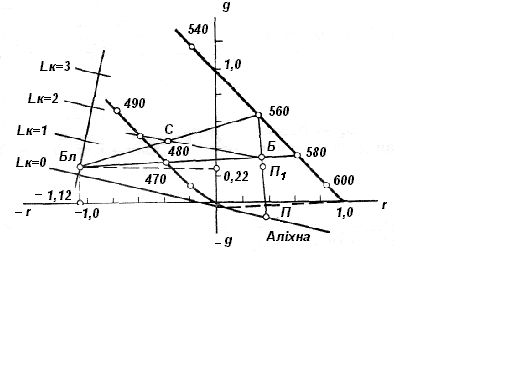
Рис. 2.19. Нереальні кольори на графіку r, g

Одиничний колір Бл – блакитний, за колірним тон тотожний спектральному ₄₈₀, але найбільш насичений.

Крім того, якби удалося одержати випромінювання уявлюваного кольору Бл та змішати його з білим, то суміш має колір монохроматичного ₄₈₀, включаючи його насиченість. Змішуючи випромінювання кольорів Бл та ₅₆₀, можна було б одержати реальний сильно насичений С того ж колірного тону, що і лежачий між ₄₈₀ і ₄₉₀. Для отримання яскравості одиничного кольору Бл необхідно: нанести на діаграму лінії яскравості і скористатися яркістним масштабом (ліва частина рисунка). Уявлюваний одиничний Бл має яскравість близько 0,2680 кд ^. м^–2, а С, отриманий додаванням уявлюваного з реальним, – близько 1,5 680 кд ^. м^–2.

Колір П – пурпурний, додатковий за колірним тоном до кольору випромінювання ₅₆₀. Змішання випромінювання нереального кольору П с жовто-зеленим _5у дало б дуже мало насичений пурпурний П₁. Найцікавіша властивість уявлюваного кольору П – відсутність яскравості: точка, що виражає цей колір, лежить на аліхні.

2.11 Колірний трикутник xyz

Колірний трикутник хуz створювався на базі колірної діаграми rg. На рис. 2.20 вона показана разом з аліхною. Вибір основних кольорів на цій лінії забезпечує їх безяркістністъ. Тому що серед кольорів RGВ найменші яскравості мають В і R, тому на аліхні обирають близькі до них X і Z. Іншими словами, сторона хz трикутника хyz повинна збігатися з аліхною. Третій основний колір Y має яскравість. Його яркістний коефіцієнт зручно прийняти рівним одиниці.

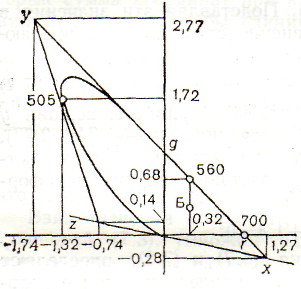
Рис. 2.20 – Положення сторін трикутника хуz, знайдене розрахунковим шляхом

В_Ч=680m(хL_х+уL_у+zL_z), з урахуванням значення яскравості коефіцієнтів (L_х=0; L_y=1; L_z=0), В_Ч=680my.

Отже, В_Ч=680Y.

Таким чином, першою метою є розробка системи, що досягається вибором двох основних кольорів на аліхні. При цьому яскравість у системі ХY визначається не модулем кольору, як у RGВ, а тільки однією координатою Y.

Досягнення другої мети трохи складніше. Так, кольори, що лежать поза трикутником, мають негативні координати. Для формування позитивних координат всіх реальних кольорів локус потрібно помістити усередину трикутника кольоровості ХYZ, обравши положення його сторін (рис. 2.20). При цьому сторона хz збігається з аліхною, тобто відповідає рівнянню g+0,208r+0,013=0.

Сторону ху раціонально вибрати дотичною до локусу. Цим досягається остання мета, поставлена при розробці системи. При такому виборі всі спектральні кольори, що лежать на цій стороні, описуються двочленним рівнянням:

З рис. 2.21 видно, що для будь-якої точки, яка лежить на гіпотенузі трикутника rgb, зберігається рівність r/(1–g)=1, відкіля r+g=1. Координата z для розглянутих кольорів дорівнює нулю і, отже, що складає z=0.

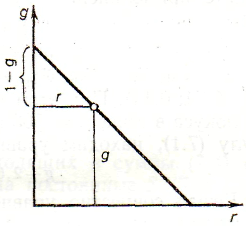
Рис. 2.21 – Ілюстрація властивостей сторони трикутника, що збігається з локусом

Для визначення рівняння сторони ху трикутника хуz (рис. 2.20) необхідно виконати наступні дії. З аналітичної геометрії відоме рівняння прямої, що проходить через дві точки:

де індекси 1 указують координати першої точки, індекси 2 – координати другої точки; x і y – поточні координати.

У позначеннях:

(2.24)

Обравши дві точки на стороні gr: одна з точок верхньої частини прямолінійної ділянки локусу, наприклад =560 нм; остання точка – =700 нм. Їх координати наведені на рис. 2.20. Тоді індекси 1 належать координатам точки ₅₆₀ (0,32; 0,68), а індекси 2 – координатам точки ₇₀₀(1;0). Підставивши ці значення у формулу (2.24), можна одержати рівняння сторони ху, що збігається з прямолінійною ділянкою локусу:

(2.25)

Сторона yz обрана таким чином, щоб координати вершин у і z: у (–1,74; 2,77), z (–0,74; 0,14). При цьому зазначена сторона майже стосується локусу в точці =505 нм. Підставивши координати у формулу (2.24), можна знайти рівняння сторони:

Враховуючи координати точок у і z, можна отримати уточнені значення:

x (1,2750; –0,2778);

y (–1,7393; 2,7673);

z (–0,7431; 0,1409).

Враховуючи дві координати кольоровості, можна знайти третю та написати наступні рівняння

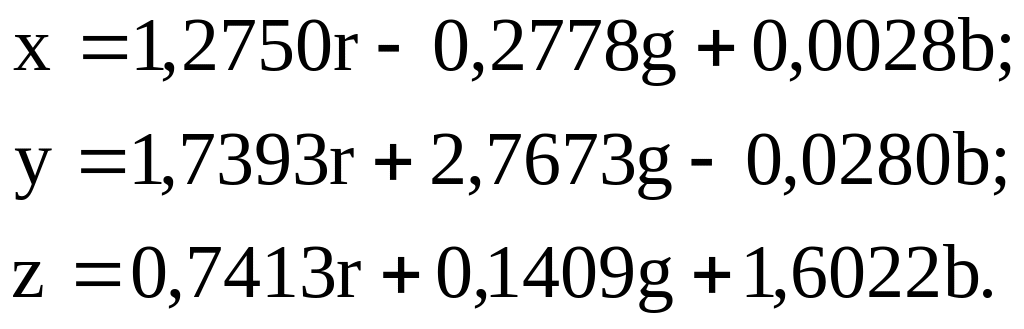(2.26)

Отриманий колірний трикутник наведено на рис. 2.20. Його варто перетворити, насамперед, тому, що біла точка не знаходиться в центрі трикутника і, отже, координати білого кольору не рівні між собою. У цьому можна переконатися, знайшовши суму х + у + z. З рівнянь (2.26) видно, що сумарний колір дорівнює:

Для розташування білої точки у центрі трикутника rgb за одиничні кількості основних прийнято різні їх яскравості, що відповідають співвідношенню L_R:L_G:L_B=1:4,59:0,06.

Цей же прийом застосовується і для зсуву білої точки до центру трикутника хуz при вирішенні задачі не експериментально, а шляхом розрахунку. Її вирішення полягає у визначенні умов, при яких сума координат при кожному з основних (рівняння 2.26) дорівнювала б одиниці:

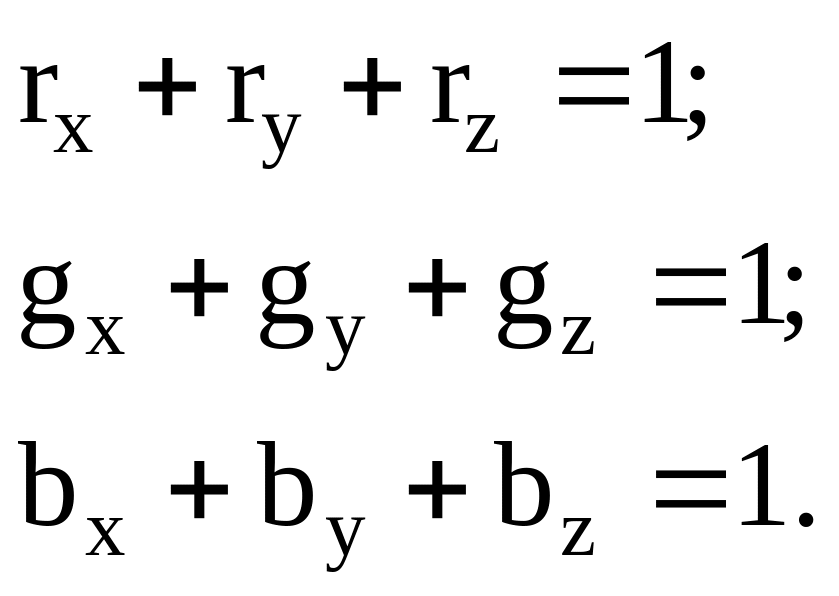(2.27)

Якщо зазначені суми дорівнюють одиниці, то:

Якщо значення координат, що входять у суми (2.27) з рівнянь (2.26), помножимо їх на постійні S, Т і U, то дорівняємо суми одиниці:

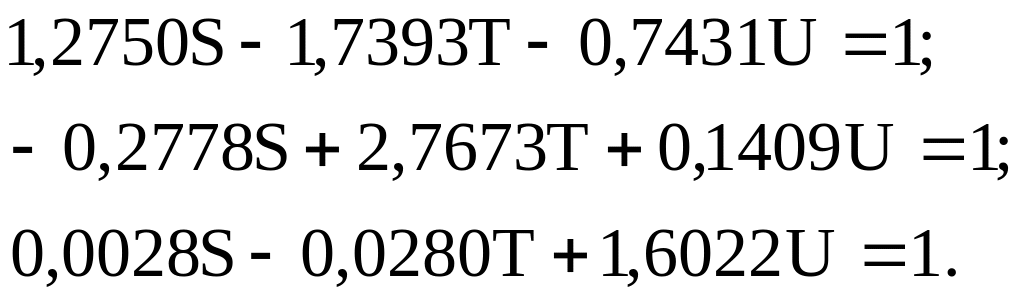
Тоді одержимо S=1,8546; T = 0,5155; U = 0,6299. Множення кожного з рівнянь (2.26) на відповідний коефіцієнт дає систему:

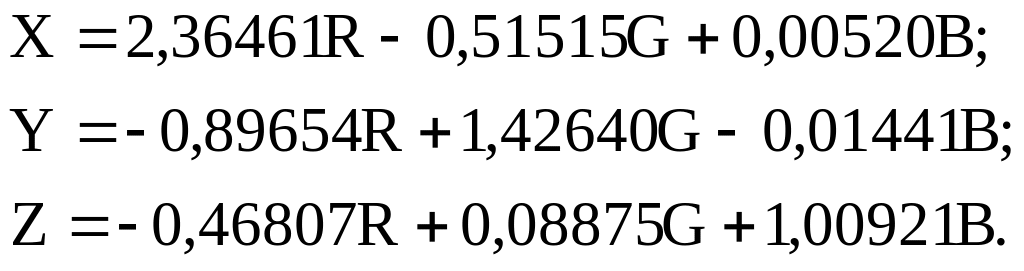(2.28)

Оскільки рівняння (2.27) дотримані, то сума основних має білий колір.

Рівняння (2.28), що зв'язують кольори ХУ і RGВ, у вигляді, в якому вони представлені вище, стандартизовані (ГОСТ 13088–67).

Проте вони не відповідають вимогам до основних X, Y, Z. Для ілюстрації цього визначимо коефіцієнти яскравостей L_х, L_у, L_z за рівняннями (2.28):

(2.29)

Для доведення L_Y до одиниці, що було однієї з задач, поставлених при розробці системи, рівняння (2.29) ділять на 5,65. Тоді формули переходу перетворюються в рівняння (2.30):

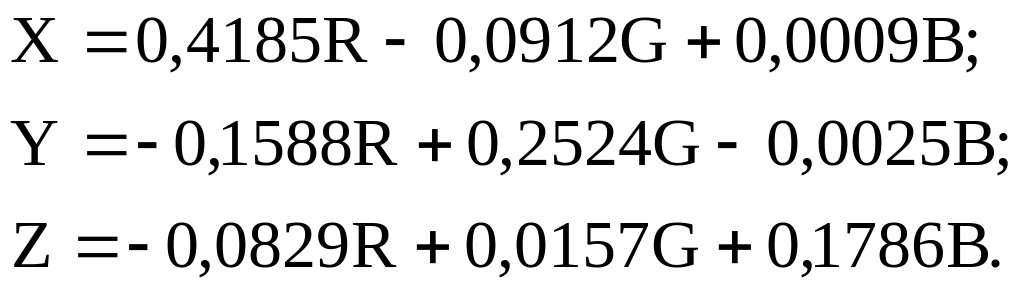(2.30)

Колірний трикутник хуz (рис. 2.20), як і трикутник rgb – непрямокутний. У результаті його проекційного перетворення одержують прямокутний трикутник з локусом, що знаходиться усередині нього, – колірну діаграму ху (рис. 2.22)

Для наочності можна колірні тони основних ХУ представити через домінуючу довжину хвилі. З'єднавши вершини трикутника з білою точкою, знайдемо точки перетинання прямих з локусом. Ці точки вказують домінуючу довжину хвилі кожного з основних. З рисунка _дx498 нм; _дy521 нм; _дz471 нм.

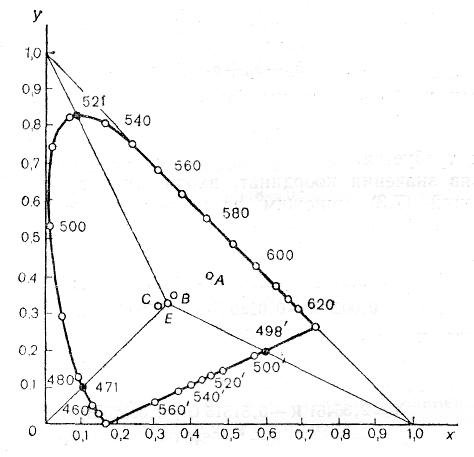
Рис. 2.22 – Колірна діаграма ху (визначення домінуючої довжини хвилі основних кольорів цієї системи)