2.6 Діаграма колірності rgb. Колориметричні властивості прямокутного трикутника
На рис. 2.15 надано трикутник кольоровості rgb з локусом і прямою пурпурних кольорів (поле реальних кольорів), що знаходяться в просторі RGB. Локус показаний на рисунку штриховими лініями, тому що знаходиться в октанті G–RВ. Спроектуємо «зображену на рисунку фігуру на координатну площину GR–R. Тоді проекція вершини b – точка b' збігається з точкою О – початок координат. Вісь Og у цьому випадку – вісь ординат декартової системи, а вісь Оr – вісь абсцис.
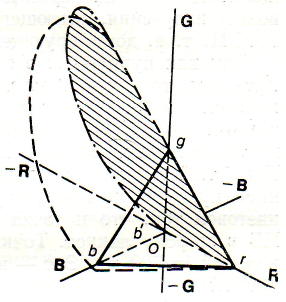
Рис. 2.15 – Проекційне перетворення трикутника rgb з локусом
Проекційно перетворене поле реальних кольорів, включаючи трикутник rgb, показане на рис. 2.15 (заштриховано). На рис. 2.16 воно сполучено з площиною креслення. Колориметричні властивості трикутника, отриманого таким шляхом, не відрізняються від властивостей вихідного рівностороннього.
Рис. 2.16 – До виразу колориметричної чистоти кольору на діаграми rg і виводу рівняння аліхни
1. Значення колірних координат кольорів не змінюються від проекційного перетворення
2. Насиченість кольорів як і раніше зростає від білої точки до локусу.
3. На прямій, що проходить через цілу точку, лежать, як і рівносторонньому трикутнику, кольоровості кольорів постійного колірного тону.
4. На прямій, що з'єднує точки двох кольоровостей, знаходяться точки їх сумарних кольорів; відстані точки сумарного кольору до точок кольорів, що складаються, модулям останніх.
5. Біла точка має, як і раніш, координати Б (1/3; 1/3).
6. Локус залишається границею спектральних кольорів.
7. Аліхна залишається лінією нульових яркостей.
Подібні проекційні перетворення в колориметрії застосовуються часто. Вони спрощують визначення і розрахунки. При них зберігаються метричні властивості не тільки трикутника, але і колірного простору. Широко використовується як ортогональне проектування, так і більш складні, як у розглянутому прикладі, випадки проекційних перетворень.
Сітка прямокутних координат з нанесеним на неї локусом, замкнутим прямій пурпурних кольорів, називається діаграмою колірності або колірним графіком.
2.7 Домінуюча довжина хвилі, колориметрична чистота, умовна чистота кольору
Вираження колірного тону через домінуючу довжину хвилі і насиченості через колориметричну чистоту. Колірний графік можна використовувати для визначення домінуючої довжини хвилі і колориметричної чистоти.
Колірний тон. Візьмемо на діаграмі кольоровості довільну точку К (рис. 2.16). Нехай вона має, наприклад, координати К (0,2; 0,6). З'єднаємо її з білою точкою і продовжимо лінію нагору до перетинання з локусом. На проведеній в такий чином прямій змінюється тільки насиченість, і точка перетинання К=550 відповідає довжині хвилі випромінювання, що має той же колірний тон, що "і колір К, тобто домінуючій довжині хвилі.
Тому що пурпурних у спектрі, а отже, на локусі немає, то для них розглянута характеристика знаходиться таким чином. Візьмемо поблизу лінії пурпурних колір П. Знайдемо колір, тотожний йому за тоном, але максимальної насиченості. Для цього з'єднаємо точку П с білою точкою і продовжимо пряму перетинання з лінією пурпурних. Точка перетинання П виражає той же колірний тон, що і точка П. Продовжимо тепер пряму ПБ убік локусу. Точка перетинання вказує довжину хвилі К=500 нм. Це – колір, додатковий до П. Його довжиною хвилі зі знаком «штрих» позначається точка П на лінії пурпурних. У нашім прикладі домінуюча довжина хвилі дорівнює 500' нм.
Колориметрична чистота кольору. Знаючи положення кольору К на діаграмі кольоровості (рис. 2.16), можна знайти його колориметричну чистоту р за формулою
(2.9)
Замінивши В + 5ВБ = В,' одержимо р = В : В.
Для розрахунку колориметричної чистоти за даними, які можна прочитати на діаграмі:
(2.10)
Перетворимо відношення m/m так, щоб до нього можна було прикласти правило додавання кольорів за формулою:
(2.11)
З огляду на те, що:
(2.12)
Узявши відношення модулів mБ/m замість відношення відрізків КК/КБ, проведемо зворотне перетворення:
(2.13)
(2.14)
де перший співмножник – відношення відстані від точки обумовленого кольору до білої до відстані від білої точки до локусу.
Розрізняють два близьких поняття – умовна чистота кольору рy і власне колориметрична чистота кольору р (іноді її позначають pк). При визначенні ру яркісні коефіцієнти виражають як 1/680 частку колориметричної одиниці основних. У цьому змісті яркісні коефіцієнти рівні між собою. Тоді:
(2.15)
При визначенні р відношення L/L виражається у світлових одиницях яскравості, і, отже,
(2.16)
Для практичних розрахунків відношення відстаней КБ/КБ заміняють пропорційним йому відношенням різностей координат, що легко прочитати по координатних осях діаграми. Наприклад, для кольору К (рис. 2.17):
(2.17)
для кольору К1:
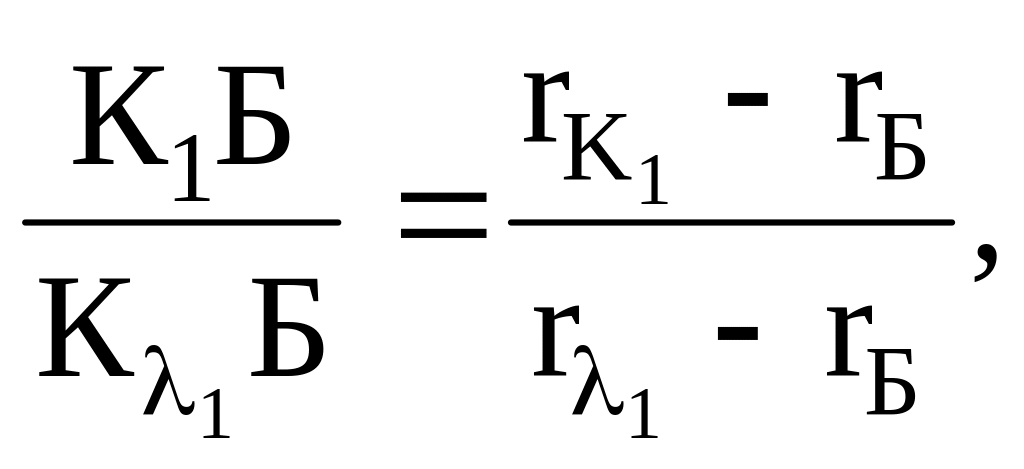(2.18)
для кольору К2 (точка К2 лежить на лінії пурпурних кольорів, збігаючись із точкою П).
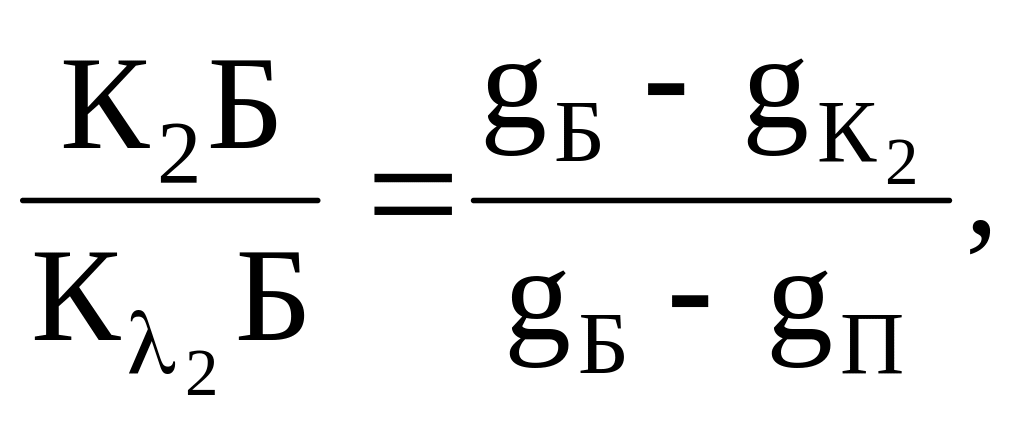(2.19)
Для кольорів, розташованих за локусом, чистота більше одиниці. Так, для К3:
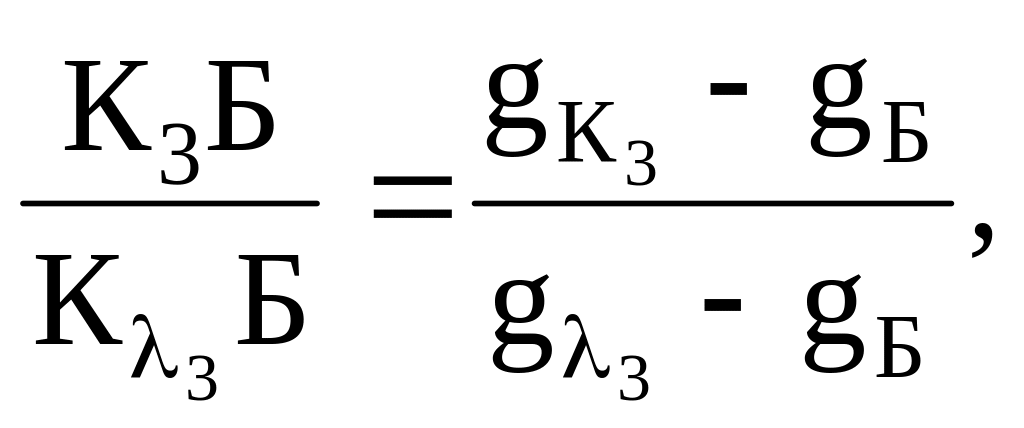(2.20)
де:
У колориметричній практиці застосовують діаграми, на яких точки кольорів однакової чистоти з'єднані лініями. Таким чином, значення цієї величини можна прочитати по діаграмі.
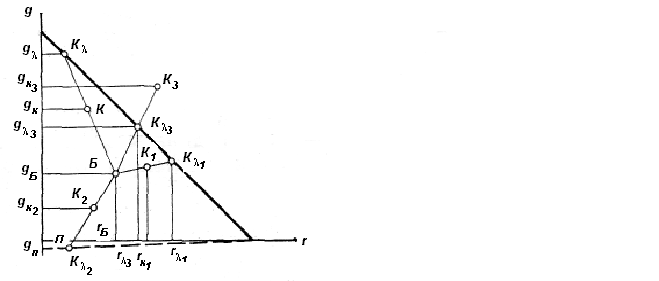
Рис. 2.17 – Схема визначення колориметричної чистоти кольору