10.2.1.1 Интегральный эффект

Интегральный эффект (W), первый показатель общей экономической эффективности.

Интегральный эффект – позволяет сравнить текущую стоимость будущих доходов от вложений с требуемыми в настоящий момент затратами. То есть все будущие доходы от инвестиций приводятся к начальному моменту времени и сравниваются с инвестиционными затратами.

Подсчитанный по формуле де­нежный поток для каждого года суммируется и находится полный денежный по­ток за время осуществления проекта (n):

. (10.10)

Денежный поток за время осуществления проекта показывает полную сумму средств, образующихся на счете предприятия за время осуществления проекта. Однако он ничего не говорит об эффективности проекта, т. к. в нем затраты и результаты разновременны и, следовательно, несопоставимы.

Для нахождения показателя интегрального эффекта (W), рассчитанные по формуле денежные потоки для каждого года реализации проекта (D_t) сумми­руются и приводятся к моменту времени начала реализации проекта с помощью коэффициента дисконтирования:

, (10.11)

где W  интегральный эффект;

D_t  денежный поток t-ro года;

r  норма дисконта времени (коэффициент приведения разновремен-ных затрат r = 0,1);

n  время реализации инвестиционного проекта.

Критерий принятия решения с помощью интегрального эффекта одинаков для любых видов инвестиций и организаций:

• если W > 0, то инвестиционный проект считается экономически выгодным и его следует принять;

• если W < 0, то инвестиционный проект нецелесообразен, и принимать его не следует.

Положительный интегральный эффект означает, что текущая стоимость доходов превышает текущую стоимость затрат и следовательно, следует ожидать увеличения благосостояния инвесторов.

Расчет интегрального эффекта сводится в таблицу 10.8. так же в данную таблице рассчитываем нарастающую итоговую выручку NPV, для вычисления дисконтированного срока окупаемости.

Таблица 10.8  Интегральный эффект W при ставке дисконта r = 0,1

Т	2012	2013	2014	2015	2016	2017	Всего
(1+r)-t	1,0000	0,9091	0,8264	0,7513	0,6830	0,6209	–
Dt	-1,10	-1,29	0,66	0,66	0,66	0,66	1,25
W	-0,70	-0,85	0,55	0,50	0,45	0,41	0,37
NPV	-0,70	-1,55	-1,00	-0,50	0,05	0,36	­–

В данном случае W>0, следовательно, согласно критерию, инвестиционный проект системы электроснабжения производственного корпуса Завода «Стройтехника» считается экономически выгодным и его стоит принять.

10.2.1.2 Внутренняя норма рентабельности

Знание лишь одного показателя интегрального эффекта недостаточно для принятия инвестиционного проекта, т.к. все инвестиции различны и по технико-экономическим характеристикам, и по целевым установкам (как краткосрочным, так и долгосрочным), и поэтому необходимо знание внутренней нормы рентабельности капиталовложений.

Внутренней норма рентабельности (Е) представляет собой ту норму дисконта, при которой величина дисконтированных доходов становится равной инвестиционным вложениям, т.е. такая норма дисконта, при которой интегральный эффект проекта становится равным нулю.

Эффективность капитальных вложений (Е) должна быть дифференцирована в зависимости от стоящих перед инвестором целей. В зарубежной практике инвесторы, в зависимости от возникающих перед ними задач, делят капитальные вложения на пять классов:

1класс  инвестиции с целью сохранения позиций на рынке, направленные на замену некоторых элементов производственного аппарата. В этом случае Е>0,05  0,06. При меньшем значении Е капитальные вложения не выгодны.

2класс  инвестиции с целью обновления основной массы производствен-ных фондов, для повышения качества продукции, E>0,12.

3класс  инвестиции с целью внедрения новых технологий, создание новых предприятий, E>0,15.

4класс  инвестиции с целью накопления финансовых резервов для осу-щест­вления крупных инвестиционных проектов, Е>0,2.

5класс  рисковые капитальные вложения с целью реализации проектов, ис­ход которых до конца не ясен, E>0,25.

Для определения внутренней нормы рентабельности используем формулу:

. (10.12)

Значение интегрального эффекта W при различных (1+Е)^-t представлены в таблице 10.9.

Таблица 10.9  Значение интегрального эффекта W при различных (1+Е)^-t

t	E
	0,1	0,12	0,15	0,17	0,2	0,22	0,25	0,3	0,4	0,5
2012	-0,700	-0,700	-0,700	-0,700	-0,700	-0,700	-0,700	-0,700	-0,700	-0,700
2013	-0,854	-0,839	-0,817	-0,803	-0,783	-0,770	-0,752	-0,723	-0,671	-0,626
2014	0,545	0,526	0,499	0,482	0,458	0,443	0,422	0,390	0,336	0,293
2015	0,495	0,469	0,433	0,412	0,381	0,363	0,337	0,300	0,240	0,195
2016	0,450	0,419	0,377	0,352	0,318	0,297	0,270	0,231	0,171	0,130
2017	0,409	0,374	0,328	0,301	0,265	0,244	0,216	0,177	0,122	0,086
Итого	0,347	0,250	0,121	0,044	-0,059	-0,121	-0,205	-0,303	-0,499	-0,620

По данным таблицы 10.9 строится график зависимости интегрального эффекта от нормы рентабельности (рисунок 10.1).

Получаем, что норма рентабельности E 0,17. E>0,15 что относится к 3-му классу капитальных вложений, где необходимы инвестиции с целью внедрения новых технологий на предприятии.

W

Е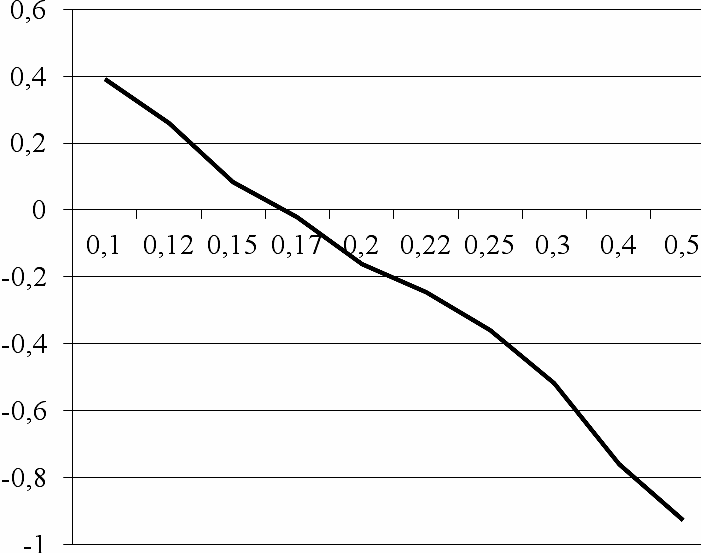

Рисунок 10.1  График зависимости интегрального эффекта

от нормы рентабельности.