4. Анализ устойчивости сар

Построим D-разбиение в плоскости параметра k₇. Решаем уравнение :

.

Подставляя в данное уравнение значения всех коэффициентов и численные значения параметров САР (см. задание) и решая его относительно

коэффициента k₅, получаем следующее выражение:

Воспользовавшись программой RADIS, определим действительную и мнимую составляющие частотной функции k₅ для ряда значений частот. В результате расчёта и построения получаем кривую D-разбиения для положительных значений частот (рис.7).

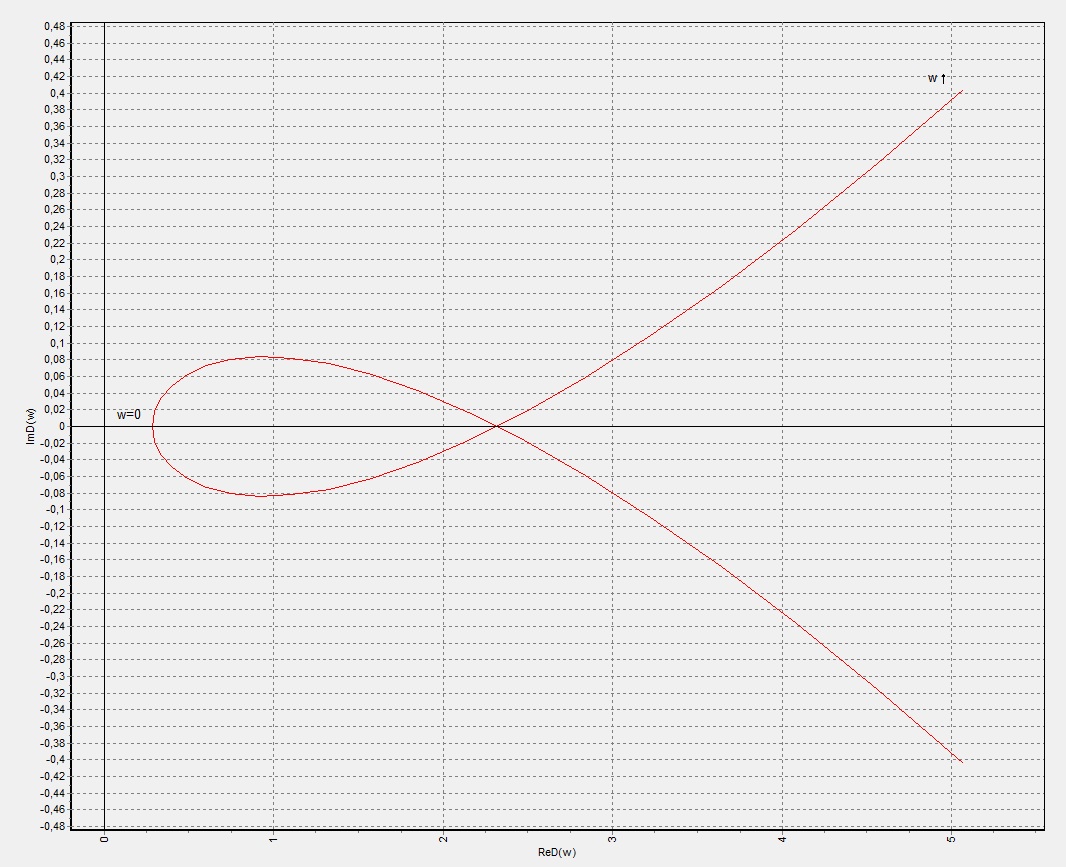
Рисунок 7 – D - разбиение в плоскости коэффициента k₅: I – область наибольшей вероятности устойчивой работы; II, III – области неустойчивой

работы САР

Кривая D-разбиения заштриховывается с левой стороны по мере возрастания частоты колебаний. Воспользовавшись правилом подсчёта корней характеристического уравнения для каждой из выделенных областей D- разбиения определяем область I , соответствующую наибольшему числу корней с отрицательной вещественной частью, т.е. более вероятную область устойчивости САР.

Для проверки устойчивости САР в области I зададимся величиной Re k₅ , взятой из этой области: k₅=0,5, и запишем характеристический полином или собственный оператор замкнутой САР с числовыми значениями коэффициентов:

.

Для проверки устойчивости САР по критерию Рауса-Гурвица составим квадратную матрицу Гурвица из коэффициентов a₀…a_n:

при проанализируем знаки диагональных миноров:

;

;

.

Все диагональные миноры положительны, следовательно, САР устойчива и область I D-разбиения является областью устойчивости САР.

Для проверки устойчивости по критерию Найквиста анализируется АФЧХ разомкнутой системы. Передаточная функция разомкнутой САР при принятых значениях коэффициентов имеет вид:

;

Вначале определяется устойчивость системы. Для этого используется собственный оператор разомкнутой САР с числовыми значениями коэффициентов:

Воспользовавшись программой Mathcad, рассчитывается и строится АФЧХ разомкнутой САР. Так как САР содержит интегратор в прямой цепи, то АФЧХ САР берет начало (при ) в вдоль мнимой оси. Из представленного на рис. 8 графика следует, что АФЧХ разомкнутой САР не охватывает точку с координатой (-1;j0), следовательно, замкнутая САР будет устойчива.

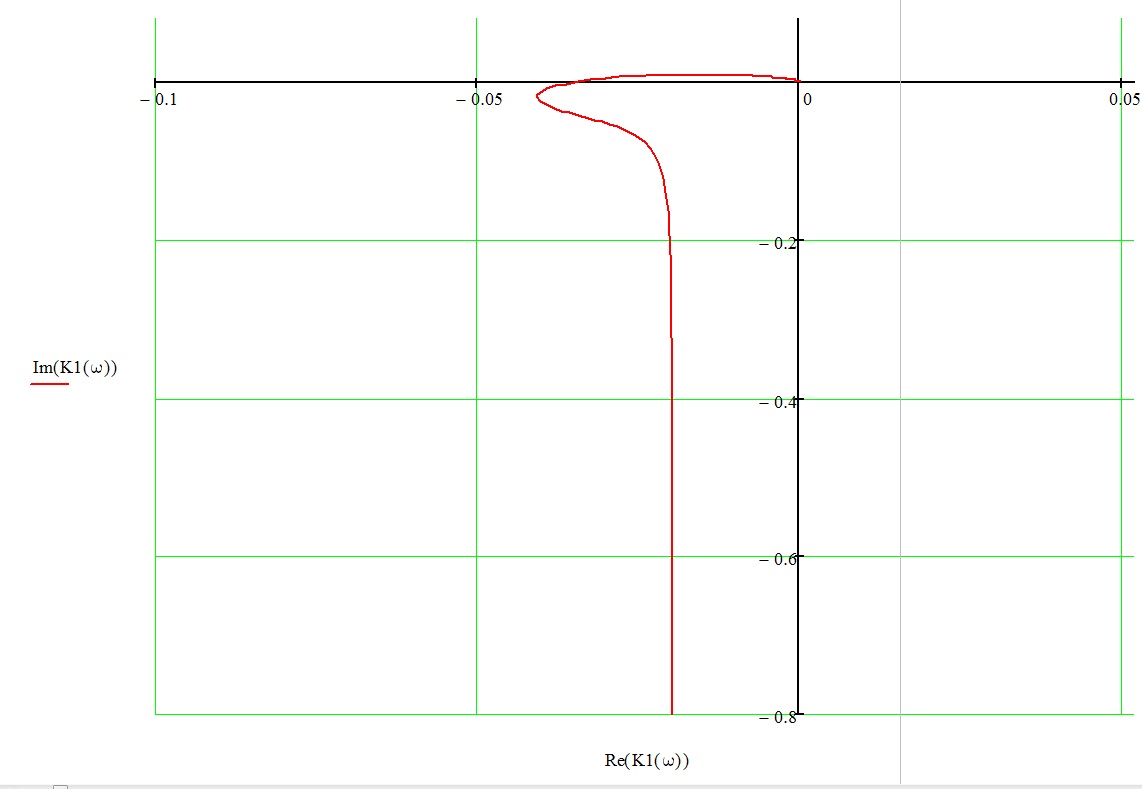
Рисунок 8 – Амплитудно-фазочастотная характеристика разомкнутой САР частоты вращения ГТД

5. Оценка качества регулирования сар

Качество регулирования САР определяется по показателям качества переходного процесса при ступенчатом управляющем и возмущающем воздействиях. Переходные характеристики рассчитываются по алгоритму и программе RADIS.

При заданных исходных данных передаточная функция замкнутой САР при управляющем воздействии имеет вид:

Задаваясь тремя значениями коэффициента k₇ из области устойчивости D- разбиения, например, k₇ =0,5; 1,5; 2,1, определяем переходные характеристики при ступенчатом возмущающем воздействии . Переходные характеристики рассчитываем по последнему выражению с использованием программы RADIS. Шаг интегрирования принимаем равным с, время интегрирования с.

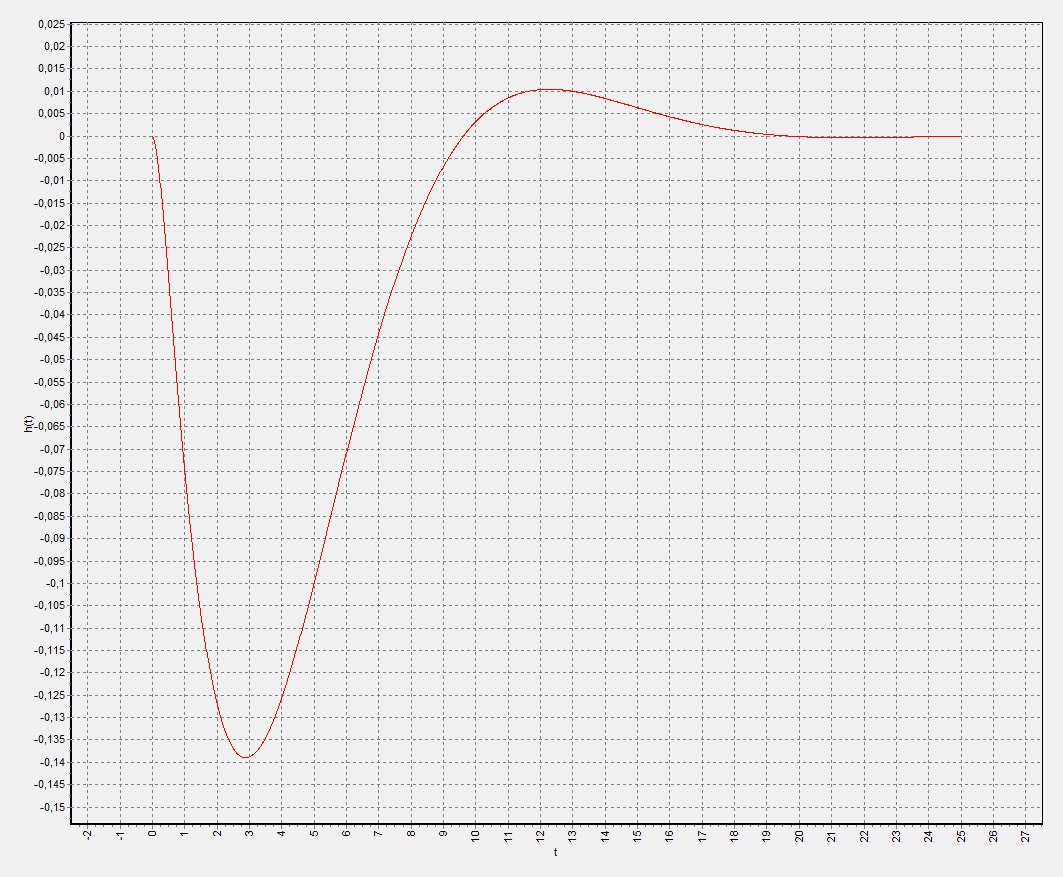
Рисунок 9 – Переходные характеристики САР частоты вращения

авиационного ТРД при k₅ =0,5

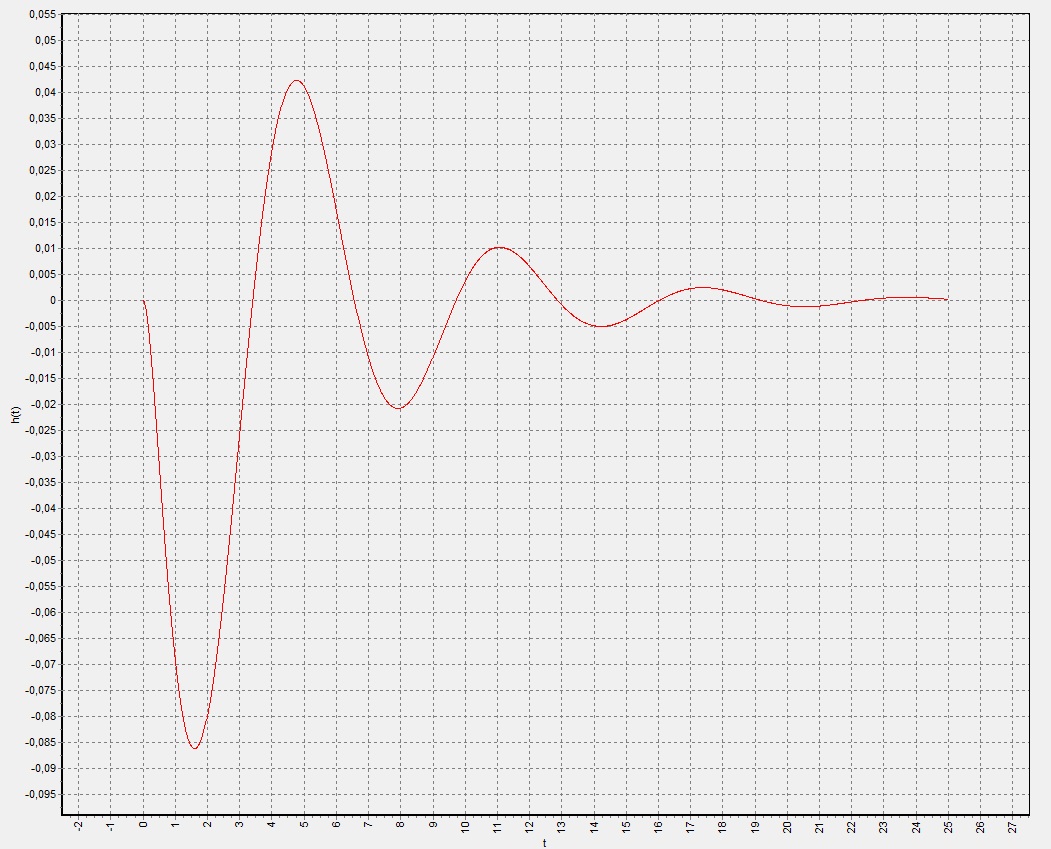
Рисунок 10 – Переходные характеристики САР частоты вращения

авиационного ТРД при k₅ =1,5

Рисунок 11 – Переходные характеристики САР частоты вращения

авиационного ТРД при k₅ =2,1

	0,138	0,087	0,075
	15	15	15,1
	1,5	2,3	2,7
	-	0,98	1,16

Из анализа графических зависимостей следует, что увеличение коэффициента усиления звена k₅ в прямой цепи регулирования САР приводит к колебательному переходному процессу и в тоже время к снижению статической погрешности поддержания заданного расхода топлива через дроссельный кран. Изменяя коэффициент k_5, можно добиться приемлемых показателей качества регулирования.