МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА

РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное образовательное учреждение

высшего профессионального образования

«Курская государственная сельскохозяйственная академия

имени профессора И.И. Иванова»

Кафедра физики и ТМ

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

по организации

самостоятельной работы студентов

по дисциплине «Физика»

Направление подготовки бакалавров: 110800 Агроинженерия

Профиль "Технологическое оборудование для хранения и переработки с.-х. продукции"

Профиль "Технические системы в агробизнесе"

Профиль "Технический сервис в АПК"

Профиль " Электрооборудование и электротехнологии "

Факультет: инженерный

Форма обучения: очная

Курск – 2011

Тема № 3 «Кинематика и динамика вращательного движения твердого тела»

Вопросы для самостоятельного изучения

(см. вопросы к гл.4,5[1] и гл. 2,4 [7] )

1. Дайте определение угловой скорости. Углового ускоре­ния. Напишите соответствующие формулы. В каких едини­цах измеряются эти величины?

2. Выведите формулу для вычисления угловой скорости при равнопеременном вращении.

3. Выведите формулу для вычисления угла поворота при равнопеременном вращении.

4.Дайте определение момента силы. В каких единицах измеряется момент силы?

5.Выведите основной закон динамики вращательного движения твердого тела.

6.Дайте определение момента инерции. В каких едини­цах измеряется эта величина? Каков ее физический смысл?

7.Дайте определение момента импульса. Выведите закон сохранения момента импульса замкнутой системы вращаю­щихся тел. Приведите примеры применения этого закона.

8.Выведите формулу кинетической энергии вращающе­гося тела.

Задания

Общие

1. Составьте глоссарий по изучаемой теме. Включите в него следующие и другие (самостоятельно подобранные по данной теме) термины: материальная точка, система отсчета, мгновенная скорость, нормальное и тангенциальное ускорение, угловая скорость и ускорение, момент силы, момент инерции, момент импульса. (ОК-1, ПК- 19 )

2. Изучите и запомните следующие формулы(ПК-1, ПК-19 )

Наименование величины или физический закон	Формула
Угловая скорость и вычисление углового перемещения по угловой скорости
Угловое ускорение и вычисление угловой скорости по угловому ускорению
Связь между линейными (v и )и угловыми ( и )величинами при вращательном движении	V=
Угловая скорость при равнопеременном вращении
Угол поворота при равнопеременном вращении
Связь между угловой скоростью а, час­тотой вращения и периодом враще­ния Т при равномерном вращении
Связь между углом поворота и числом оборотов N
Основное уравнение динамики враща­тельного движения (связь между угло­вым ускорением, моментом силы М и моментом инерции J вращающегося те­ла)
Моменты инерции некоторых тел а) материальной точки массой m на расстоянии г от оси вращения
б)полого цилиндра радиусом R
в)сплошного цилиндра или диска ра­диусом R
г) однородного тонкого стержня дли­ной а относительно оси, проходя­щей через его конец
Момент импульса L
Закон сохранения момента импульса
Кинетическая энергия вращающегося тела

3. Разберите самостоятельно следующие задачи (ОК-1, ПК- 1, ПК-3, ПК-19 )

ЗАДАЧА № 1

Цилиндрический барабан ультрацентрифуги, применяю­щийся для разделения высокомолекулярных соединений, имеет диаметр 20 см и массу 5 кг. Для остановки барабана, вращающегося с частотой 9000 об/мин, к нему, после вык­лючения электродвигателя, прижали тормозную колодку. Какую силу трения нужно' приложить к боковой поверхно­сти барабана, чтобы остановить его за 20 секунд? Сколько оборотов он сделает до полной остановки? Какова будет работа силы трения?

Решение

2R=20 см = 0,2 м m=5 кг

v₀=9000 об/мин=150 t=20 с

_

N=?F = ?A = ?

Момент силы трения, при­ложенной к поверхности бара­бана M = FR. Считая барабан сплошным цилиндром, можно написать, что его момент инер­ции равен

J =

N=?F=?A=?

Из основного уравнения динамики вращательного движе­ния следует, что M = J, где е — угловое ускорение. Следо­вательно,

_{FR= и F=} (1)

Угловая скорость тела, вращающегося с угловым ускоре­нием вис начальной скоростью . по происшествии времени t от начала движения будет равна: . Так как ба­рабан по условию задачи останавливается, то . Поэто­му 0= . Отсюда

Подставляя это выражение в формулу (1), получим:

F= (2)

(знак минус означает, что сила замедляет вращение бара­бана).

Считая вращение барабана равнозамедленным, можно написать, что величина угла поворота

Но так как , то

(3)

С другой стороны, угол поворота связан с полным чис­лом оборотов барабана соотношением

(4)

Приравнивая правые части выражений (3) и (4), полу­чаем:

Откуда (5)

Работа силы трения, необходимая для полной остановки, барабана, будет равна его кинетической энергии, т. е.

(6)

Проверим размерности формул (2) и (6)'.

Таким образом, полученные формулы дают правильные размерности силы и работы.

Сделаем подстановку числовых значений заданных вели­чин:

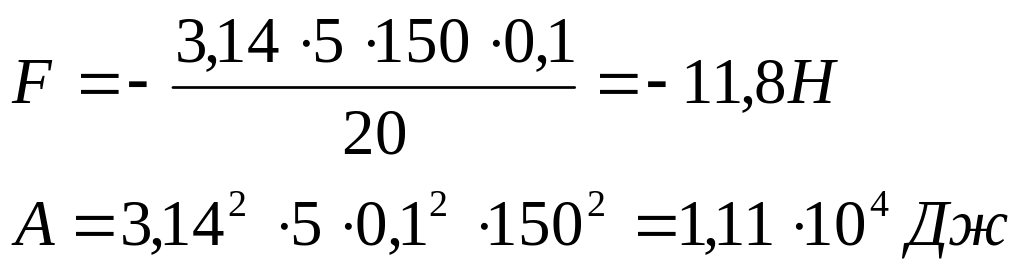
ЗАДАЧА № 2

Горизонтальная платформа массой 150 кг вращается во­круг вертикальной оси, проходящей через центр платформы, делая 6 об/мин. Человек массой 60 кг стоит при этом на краю платформы. С каким числом оборотов будет вра­щаться платформа, если человек перейдет от края платфор­мы к ее центру? Считать платформу круглым однородным диском, а человека — точечной массой.

Решение

m = 150 кг На основании закона сох-

- ранения момента импульса

60 кг можно записать:

,

- ? где J — момент инерции платформы с человеком, стоящим на ее крае, а — момент инерции платформы с человеком в ее центре.

Считая платформу однородным диском и человека то­чечной массой, можно написать:

Так как момент инерции точечной массы, находящейся в центре вращения платформы, равен 0, то

Таким образом , так как , то

.

Отсюда ,

Подставим числовые значения:

Итак, число оборотов платформы возрастет и станет 0,45 с

ЗАДАЧА № 3

Косилка - измельчитель предназначена для скашивания тра­вы и одновременного измельчения кормов для скота, Зависи­мость угла поворота барабана косилки КС-1 от времени да­ется уравнением:

=A+Bt+Ct², где В=0,6 рад/с и С=0,25 рад/с².

Найти угловую скорость вращения барабана и линейную скорость точек на его поверхности через 10 с от начала враще­ния. Диаметр барабана 0,5 м.

Решение

Угловая скорость есть

производная углового переме-

щения по времени

м Подставляя числовые данные получим:

_________________

=

Линейная скорость

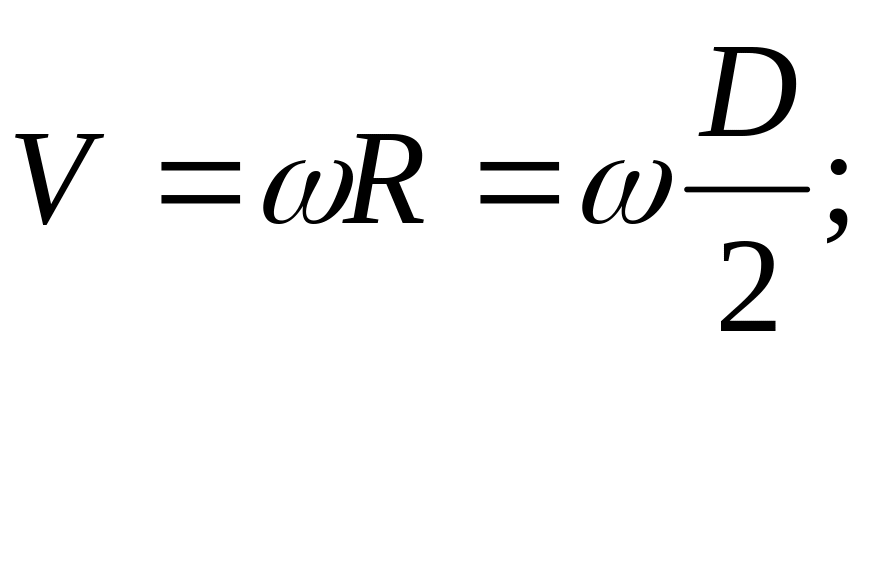
Угловая скорость равна 5,6 рад/с, и линейная скорость равна 1,4 м/с.

Задача 4

Через блок радиусом 4 см перекинули шнур, к концам которого привязаны грузы массами 50 г и 60 г. При этом блок пришел в движение с угловым ускорением 1,5 с^-2. Определить момент инерции блока. Трение при вращении не учитывать .

Решение. Воспользуемся основными уравнениями динамики поступательного и вращательного движений. Для этого рассмотрим силы, действующие на блок и на каждый груз в отдельности. На первый и второй грузы действуют силы тяжести и натяжения нити: m₁g, T₁, m₂g, T₂. На блок моменты сил M₁=T₁r и M₂=T₂r (при этом M=I), где соответственно:

T₁ и T₂ – силы натяжения нити, действующие на грузы и на блок ;

I – момент инерции блока;

 – угловое ускорение.

Составим уравнения движения каждого из тел системы «грузы – блок» в векторной форме:

;

;

а из основного уравнения динамики вращательного движения получим:

.

Спроецируем первые два уравнения на ось x, которую направим вертикально вниз. С учетом знаков проекций будем иметь:

;

;

.

С учетом того, что нить нерастяжима и не проскальзывает по блоку, получим a₁=a₂=a, a=r и тогда написанные выше уравнения перепишем в виде:

;

;

.

Решая систему трех уравнений с тремя неизвестными, найдем интересующий нас момент инерции

.

После проверки размерностей левой и правой частей, полученного соотношения и подстановки численных значений, входящих в него величин, будем иметь

кгм².

Ответ: I=2,5210^-3 кгм².

Индивидуальные задания

1. Решите задачу из задачника [2] (ПК-1, ПК-3) № 1,46; 1,47; 3,8; 3,10; 3,15; 3,16; 3,20; 3,21; 3 35; 3.36.

Тема № 4 «Уравнения неразрывности и Бернулли. Вязкая жидкость.»