5. Біртекті және біртекті емес жылуөткізгіштік теңдеулерге қойылған шекаралық есепті Фурье әдісімен шешу.

Мына -цилиндрде біртекті жылу өткізгіш

(4.9)

теңдеудің бірінші текті шекаралық

(4.10)

шарттарды және

(4.11)

бастапқы шартты қанағаттандыратын регулярлық шешімін табу керек.

Есептің шешімін

(4.12)

түрінде іздеп, оны (4.9) теңдеуге қойсақ, нәтижеде

(4.13)

(4.14)

екінші ретті бір-біріне тәуелсіз екі біртекті жай дифференциалдық теңдеулер аламыз.

Ал (4.12) шешімді есептің (4.10) шекаралық шарттарына қойып, (4.14) теңдеуді шешу үшін

(4.15)

біртекті шекаралық шарттар аламыз. (4.14)-(4.15) Штурм-Лиувиль есебі, ал оның меншікті сандары мен меншікті функциялары:

. (4.16)

Бұл меншікті сандарды (4.13) теңдеу-лерге қойып, ол теңдеудің

(4.17)

шешімдерін анықтаймыз.

Олай болса (4.9)-(4.11) есеп формалды шешімі

(4.18)

түрінде болады, мұндағы - белгісіз еркін коэффициенттер; оларды есептегі (4.11)-бастапқы шарт орындалатындай таңдаймыз, яғни (4.18) шешімді (4.11) шартқа қойып

өрнегін аламыз. Егер бұл өрнекті функцияның синус функция бойынша Фурье қатарына жіктелгені деп қабылдасақ (ол заңды, себебі ) онда

(4.19)

Фурье коэффициенті ретінде анықталады. Міне осы (4.19) коэффициент мәнін (4.18) өрнекке қойып (4.9) – (4.11) есептің тұрпаттама шешімін

(4.20)

аламыз, мұндағы

. (4.21)

3. Біртексіз есеп: - цилиндрлік аймақта (4.22)

теңдеуді

(4.23)

шекаралық және

(4.24)

бастапқы шарттарды қанағаттандыратын шешімін табу керек.

Есептің шешімін

(4.25)

түрінде іздейміз; мұндағы функцияны (яғни түріндегі белгілі функция) шарт-тарды қанағаттандыратындай таңдап аламыз, ал - жаңа белгісіз функция

, (4.26)

(4.27)

(4.28)

есептің шешімі.Бұл (4.26)-(4.28) есептің шешімін түрінде қарастырамыз, мұндағы - жоғарыдағы (4.9)-(4.11) есептің шешімі ((4.20) формула бойынша):

, (4.29) ал функция мына (4.30)

есептің шешімі. (4.30) есеп шешімін

(4.31)

түрінде іздейміз; ал (4.30) есептегі белгілі функцияны да бойынша қатарға жіктеп:

(4.32)

қатарды және (4.31) өрнектерді (4.30) есепке қойып, ондағы белгісіз функцияларды анықтайтын

(4.33)

Коши есебіне келеміз. Бұл жердегі (4.31)-(4.32) қатарлардағы функциялар (4.9)-(4.11) есептегі Штурм-Лиувиль есебінің меншікті функциялары. Ал (4.33) –Коши есебінің шешімі

. (4.34)

Бұл (4.34) шешімді (4.31) өрнекке қойып (4.30) есептің шешімін, ал оны (4.29) шешімге қосып біртексіз (4.22)-(4.24) есеп шешімін аламыз:

(4.35)

мұндағы

,

ал

6. Гармоникалық функциялардың қасиеттері.

Гармоникалық функция дегеніміз Лаплас теңдеуін қанағаттандыратын, екі рет үзіліссіз дифференциалданатын функциялар, мұндағы - Лаплас операторы.

1. Қарапайым қасиеттері

1-теорема. (Нормалдық туындының интегралы). Егер аймақтағы -гармониялық функция болса, онда ол аймақ шекарасында

. (5.17)

Дәлелдеуі. Теорема шарты бойынша , яғни үшін Грин формулалары орынды: 1-Грин формуласынан деп, ал - гармониялық функция екенін ескерсек, онда алынады; демек 1-теорема дәлелденді.

Салдар. Егер Лаплас теңдеуі үшін Нейманның ішкі есебін

қарастырсақ, онда осы есептің шешілуі үшін

(5.18)

орындалуы қажетті.

Ескерту. Бұл (5.18) шарт сыртқы Нейман есебі үшін де есептің шешілуінің де қажетті шарты болады, бірақ кеңістікте бұл шарт орндалуы міндетті емес.

2-теорема (дифференциалданатыны). Егер функция аймақта гармониялық болса, ол сол аймақта шексіз дифференциалданады.

Дәлелдеу. Шекарасы болған аймақты алайық. Бұл аймақта гармониялық функция

интегралдық өрнекті қанағаттандырады.

Егер болса, онда (себебі ) үшін. Сондықтан интеграл астындағы өрнек үзіліссіз; олай болса оны (яғни интгералды) айнымалы бойынша шексіз дифференциалдауға болады.

3-теорема (орта мәні туралы). Егер функция - шарда гармониялық және тұйық сферада үзіліссіз болса, онда функцияның сферадағы орта мәні сол сфераның центріндегі мәніне тең, яғни

(немесе ).

Дәлелдеу. - шарда гармониялық функция үшін

(5.19)

интгералдық өрнек орынды.

Ал - сфера үшін

(5.19´)

(5.19) сфераға нүктедегі - сыртқы нормаль бойынша туынды

(5.20)

Бұл алынған (5.19´)-(5.20) өрнектерді (5.19)-ға қойып

мұндағы және оң жақтағы бірінші интеграл 1-теорема бойынша нөлге тең. 3-теорема дәлелденді.

!!!!!Это на всякий случай первая и вторая формула Грина,вдруг спросят!!!!!

,

7. Лаплас теңдеуі үшін шеттік есептің қойылуы және шешімдердің жалғыздығы.

Лаплас теңдеуі

,

- айнымалы, - параметрлі нүктелер; - және векторлардың скаляр көбейтіндісі; 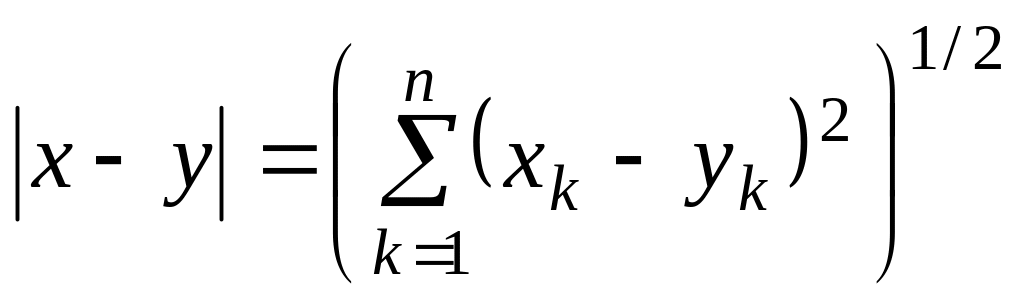- және нүктелердің ара қашықтығы деп қабылдаймыз.

Бір байланысты бет ( жағдайда) аймақты - ішкі және - сыртқы, шексіз нүктелерді қамтитын аймақтарға ажыратады. Шенелген аймақ шекарасын (немесе ) әрпімен белгілейік; деп сол бетке сырттай тұрғызылған - бірлік вектор, мұндағы - вектордың бағыттаушы косинустары.

Егер болып Лаплас теңдеуін аймақта қанағаттандырса, оны Лаплас теңдеуінің регулярлық шешімі деп айтады; оны әдетте гармониялық функция дейді. Ал, егер Лаплас теңдеуінің шешімі функция шексіздік нүкте төңірегінде: жазықтықта шенелген, ал кеңістікте түрінде баяу азайса ( ұмтылғанда), яғни жалпы жағдайда болса, онда функцияны шексіздікте регулярлықта деп айтады.