25

48. Екінші ретті дербес туындылы дифференциалдық теңдеудің классификациясы және канондық түрі.

Екінші ретті айнымалы немесе тұрақты коэффициентті сызықтық дербес туындылы теңдеу, жалпы түрде, мәселен, екі аргумент функция үшін

(1.12)

түрінде береді, мұндағы және белгілі жатық функциялар.

1. Теңдеуді сараптау

а) - (1.12) теңдеудегі екі аргументті болсын;

Теңдеудің коэффициенттерінен дискриминантты есептейміз, егер болса, онда (1.12) теңдеу гиперболалық, болса – эллиптикалық, ал болса, параболалық теңдеулер болады.

б) (1.12) теңдеудегі - аргументі болса, яғни ол теңдеу мына

(1.13)

түрде болады, онда (1.13) теңдеуге сәйкес жоғарғы туындылы мүшелерінен

(1.14)

квадраттық форманы түземіз, мұндағы - теңдеу анықталған аймақтағы тұрақтандырылған кез келген нүкте.

Ол (1.14) квадраттық форманы ерекшеліксіз түріндегі түрлендіру нәтижесінде оны - квадраттық форманың канондық түріне келтіреді, мұндағы және , .

Егер барлық болып бір таңбалы болса, онда (1.13) теңдеу эллиптикалық, ал болып ең болмағанда біреуі қалғандарына кері таңбалы болса, онда (1.13) – гиперболалық; ал енді ішінде ең болмағанда біреуі нөлге тең болса, онда ол теңдеу параболалық болады.

Екінші реттік (1.12) теңдеуді канондық түрге келтіру

Жаңа, (еркін түрде) айнымалылар

(1.15)

енгізейік. Бұл жаңа айнымалы алмастыру ерекшеліксіз деп, яғни алмастыру якобианы

(1.16) деп қабылдайық.

Бұл жаңа айнымалы енгізген жағдайда күрделі функция болады, сондықтан

(1.17)

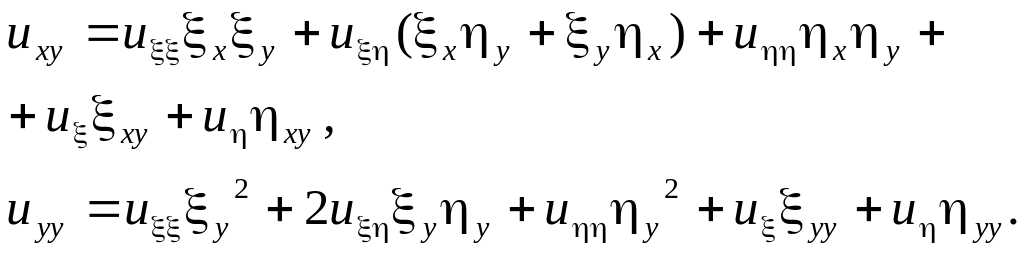
Бұл (1.17) туындыларды (1.12) теңдеуге қойып,

(1.18) теңдеуді аламыз, мұндағы

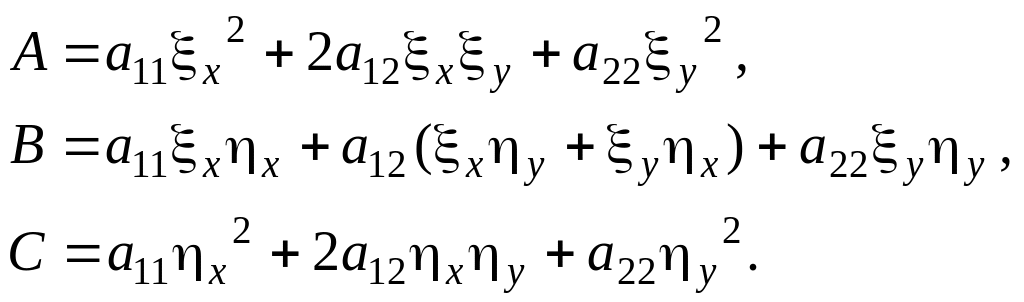(1.19)

Жоғарыдағы (1.15) алмастырудың еркіндігін пайдалану қажет. Сондықтан (1.18) өрнектегі болатындай етіп, жаңа алмастыру (1.15) таңдайық. Ал, және деген теңдеулер жаңа айнымалылар мен мына

(1.20)

теңдеудің шешімдері ретінде алу деген жағдай. Мына жай дифференциалдық теңдеу

. (1.21)

(1.20) теңдеуге сәйкес келген жоғарыдағы (1.12) теңдеудің сипаттаушы теңдеуі, ал оның шешімдері сипаттаушылары деп аталады.

Сол (1.12) теңдеудің коэффициенті деп қабылдап, (1.21) теңдеуді туынды арқылы шешейік, онда . (1.22)

Міне осы теңдеудің шешімдері (интеграл-дары) жоғарыдағы (1.15) алмастыру өрнектерін анықтайды. Енді сол айнымалылар түрлерін (1.12) теңдеудің қайсы түрге (типке) жататын байланысты анықтап, (1.12) теңдеуді канондық түрге келтірейік.

I. (1.12) теңдеу гиперболалық болсын, онда . Жай дифференциалдық (1.22) теңдеулердің нақты айнымалы, сызықты тәуелсіз екі шешімдері болады. Міне осы шешімдер

(1.15)

гиперболалық (1.12) теңдеуді (1.23)

канондық түрге келтіреді. Бұл теңдеуді шамаға бөліп, одан кейін деп тағы да алмастыру енгізсек, онда (1.23) теңдеу

(1.23')

кәдімгі гиперболалық теңдеудің канондық түріне келтірілген болады.

II. (1.12) теңдеу эллиптикалық болсын, онда болып, (1.22) жай дифференциалдық теңдеудің

(1.24)

түріндегі комплекс айнымалы шешімдері болады. Егер жаңа айнымалыны (1.24) шешімінен түрінде алып (жоғарыдағыдай) алмастырсақ, онда (1.18) мына

теңдеуге айналады, бірақ мұндағы мен комплекс айнымалы болады. Ал, канондық теңдеу нақты айнымалыда болсын деп мақсат қойсақ, онда жаңа айнымалы үшін (1.24) шешімдердегі

жаңа айнымалыларды таңдаймыз. Бұл жағдайда

екенін ескерсек, онда (1.18)

канондық түрге келеді.

III. (1.12) теңдеу параболалық болсын, онда болып (1.22) теңдеудің бір-біріне тең бір ғана нақты айнымалы шешімі болады.

Бұл жағдайда жаңа айнымалы үшін - алынған шешім, ал екіншіні - еркін түрде, бұл екеуін түрлендіру Якобианы нөлге тең емес (яғни сызықтық тәуелсіз) болатын етіп таңдап алады.

Нәтижеде, (1.18) теңдеу параболалық болған жағдайда, немесе канондық түрлеріне келтіріледі.

1-ескерту. Егер функция көп аргументті болса, онда бұларда мына төмендегі канондық түрлерге гиперболалық теңдеу

; параболалық теңдеу

; эллиптикалық теңдеу

келтіріледі, бұлардағы Лаплас операторы делінеді.

2-ескерту. Кейбір жағдай жоғарыда келтірілген канондық теңдеулерді бірден интегралдау (шешу) мүмкін болмайды, себебі, теңдеуде функцияның өзі және бірінші туындылары ыңғайсыз араласып келеді. Бұл жағдайдағы канондық теңдеуді түрінде алмастыру енгізіп, теңдеудегі ыңғайсыз мүшелерді еркін тұрақтылар мен -лерді әртүрлі таңдау нәтижесінде интегралданатын түрге келтіруге болады.

3-ескерту. Екінші ретті жай дифференциал-дық теңдеулердің жалпы шешімі екі еркін тұрақты шамаларға тәуелді болса, ал дербес туындылы теңдеу үшін жалпы шешім ұғымы енгізілмейді. Бірақ, кейбір түрлендірулер нәтижесінде екінші ретті дербес туындылы теңдеу бір аргумент бойынша екі рет интегралдау нәтижесінде шешім алынады. Бұл жағдайда жай дифференциалдық теңдеу теориясы секілді жалпы шешім ұғымы пайда болады, ол екі еркін функцияға тәуелді болады.

1. Біртекті толқын теңдеуі үшін Коши есебі. Дюамель қағидасы..

аймақта

(1.1)

Теңдеудің бастапқы шарттарын (1.2)

(1.3)

Қанағаттандыратын регулярлық шешімін табу керек.

(1.1) теңдеудің сипаттаушы теңдеуі

Оның сипаттаушылары , . Егер , алмастыруын жасасақ, онда (1.1) теңдеудің екінші канондық формасы (1.4) теңдеуін аламыз. Теңдеу (1.4) жалпы шешімі түрінде жазылады. Кері түрлендіру жасап, (1.1) теңдеудің жалпы шешімін

(1.5) түрінде жазуға болады. Мұнда толқын жылдадықпен оң бағытта, ал кері бағыттығы қозғалысын сипаттайды. Белгісіз пен функцияларын бастапқы шарттарды пайдалынып табамыз:

, немесе

.

Осы теңдіктерден

.

Табылған пен функциялары (1.5) теңдікке қойсақ, онда

(1.6)

Даламбер формуласын аламыз. Егерде функция , болса, онда (1.6) формуламен анықталған функция және (1.1)-(1.2)-(1.3) Коши есебінің регулярлық шешімі болатынын тексеру қиын емес.

Дюамель қағидасы. Дюамель қағидасы біртекті Коши есебінің шешімін біле отырып, біртекті емес теңдеудің де шешімін табуға көмектеседі. Біртекті емес толқын теңдеуі үшін коши есебі.

аймақта біртекті емес теңдеудің (1.7)

Бастапқы шарттары (1.8)

Болатын регулярлық шешімін табу керек. Қойылған (1.7)- (1.8) Дюамель қағидасын пайдаланып отырып шешеміз. Дюамель қағидасы бойынша мынадай көмекші есепті құрамыз

(1.9)

(1.10)

. (1.11)

Егерде көмекші (1.9)- (1.10)- (1.11) есептің шешімі болса, онда Дюамель қағидасы бойынша бастапқы (1.7)- (1.8) есептің шешімі (1.12)

теңдікпен анықталады. Тексеріп көрейік. (1.12) теңдіктен болады. Туындысы шарт (1.10) ескерсек, онда . (1.13)

Осыдан . (1.12) теңдікті аргумент бойынша 2-рет, ал (1.13) теңдікті бойынша бір рет дифференциалдап мына теңдіктерді

аламыз. Енді (1.9)- (1.11) ескерсек, онда

Яғни (1.12) интегралмен анықталған функция теңдеу (1.7) және нөлдік шарттар (1.8) қанағаттандырады. Сонымен (1.7) -(1.8) Коши есебі шешімін табу үшін көмекші есеп (1.9) (1.10) -(1.11) шешімін табу керек. Көмекші есептің бастапқы шарты түзуінде берілгендіктен Даламбер формуласынан

(1.14)

Болады. Теңдік (1.14) оң жағын (1.12) формуласына қойсақ, онда (1.7)- (1.8) есептің шешімі

(1.15) формуламен анықталады.

Егерде функция болса, онда және онда (1.7)- (1.8) есептің шешімі.

Жалпы түрде берілген Коши есебі біртекті емес (1.7) теңдеудің бастапқы шарттары (1.2)- (1.3) болатынын есептің шешімі (1.6) мен (1.15) теңдіктердің қосындысынан тұрады. Қорытқанда мына тұжырымдамаға келеміз:

Теорема. Егер функция , , болса, онда жалпы қойылған Коши есебінің регулярлық шешімі мына формуламен

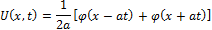
(1.16) анықталады.

2. Толқын теңдеуге қойылған аралас шекаралық есепті Фурье әдісімен шешу.

Штурм-Лиувиль есебінің меншікті функциялар жүйесі салмағымен , кеңістігінде толық жүйе. Жалпы жағдайда да кеңістікте меншікті мән мен меншікті функциялар туралы есеп.

(1.5)

(1.6)

эквивалентті симметриялық интегралдық теңдеуге келтіруге болады. Ғылыми еңбектерде эллиптикалық өзіне-өзі түйіндес оператор үшін негізгі шекаралық есептердің Грин функциясы бар және біртекті емес теңдеудің шешімі,

(2.11)

формуламен өрнектелетіні дәлелденген. Грин функциясы симметриялы, яғни (2.11) теңдікті пайдалансақ, онда (1.5)-(1.6) есепке сәйкес

(2.12)

интегралдық теңдеуді аламыз. Симметриялық теңдеуге келтіру үшін (2.12) теңдеудің екі жағын да көбейтіп, мына белгілеулерді

,

енгізіп, эквиваленті симметриялық интегралдық теңдеу

(2.13)

аламыз. (2.13)-теңдеу үшін жоғарыда келтірілген тұжырымдардың бәрі орындалады.

Фурье әдісімен шекаралық есептерді шешу жоғрыда (1.5)-(1.6) меншікті мәндер мен меншікті функциялар есебінің нөлдік емес шешімдерінің бар екенін, меншікті мәндері санаулы жиын құрайтынын, оларды өсуі бойынша келесі түрде жазуға болады:

Ал меншікті функциялар салмағымен толық ортогоналдық жүйе құрайтыны, функция ортогоналдық жүйе бойынша регулярлы жинақталатын Фурье қатарына жіктелетіні дәлелденді. Дәлелденген тұжырымдарды пайдаланып біртекті және біртекті емес гиперболалық, параболалық және эллиптикалық 2-ретті дербес туындылы теңдеулер үшін шекаралық есептерді Фурье әдісімен шешуге болады.

1. Біртекті гиперболалық теңдеу үшін (11)-(12)-(13) есепті шешу.

Шекаралық есеп. Шекарасы S облыс теңдеудің

(3.1)

бастапқы шарттар:

, (3.2)

шекаралық шарт:

(3.3)

орындалатын регулярлық шешімін табу керек .

Есептің шешімін Фурье әдісі бойынша,

түрде іздейміз. (3.1)-теңдеуге қойсақ, онда

айнымалыларды бөліп, меншікті мән қасиеттерін ескеріп

теңдігін аламыз. Осыдан мына теңдеулер

(3.4)

(3.5)

ал шекаралық (3.3) шарттан

(3.6)

теңдігі шығады.

Есептің (3.5)-(3.6) нөлдік емес шешімдері бар, олардың саны санаулы жиын құрайды. Меншікті мәндер болсын, ал меншікті функциялар

(3.7)

теңдеу (3.4) параметр деп алсақ, жалпы шешімі

түрде жазылады. тұрақты сандар.

Біртекті теңдеудің (3.1) дербес шешімдері болатынын көрсетуге болады, ал жалпы шешімін,

(3.8)

түрде аламыз. - белгісіз коэффициенттер.

Қатар (3.8) анықталған функция теңдеу (3.1) мен шекаралық шартты (3.3) қанағаттандырады. Белгісіз коэффициенттерді (3.2) бастапқы шарттардан табамыз. Бастапқы шарттарды пайдалансақ, онда

осы теңдіктер жүйе (3.7) ортогоналды болғандықтан, белгісіз коэффициенттер мына формулалармен анықталады:

,

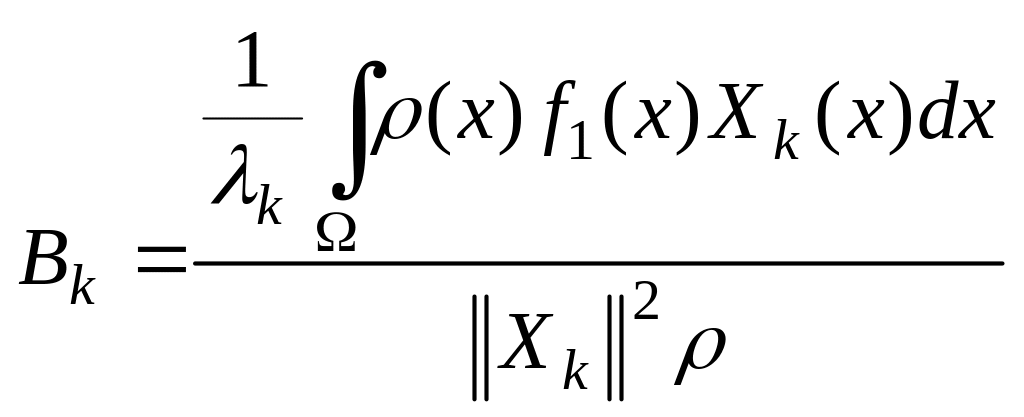
Коэффициенттерді (3.9)-теңдікке қойып, (3.1)-(3.3) есептің шешімін табамыз.

2. Фурье әдісімен біртекті емес теңдеу үшін шекаралық есептерді шешу.

Есеп. Біртекті емес теңдеу:

(3.9)

бастапқы шарттар:

, (3.10)

шекаралық шартты (3.3) қанағаттандыратын регулярлық шешімін табу керек. Уақыттың әрбір мәнінде шешімін Стеклов В.Н. теоремасы бойынша келесі қатар түрде іздеуге болады:

(3.11)

Белгісіз коэффициент,

(3.12)

функция үшін (3.6) шарт орындалғандықтан (3.12) қатармен анықталған функция шекаралық шартты (3.9) қанағаттандырады. Белгісіз табуға көшейік, ол үшін берілген функция ортогоналдық жүйе шектелсін.

(3.13)

(3.9) теңдеудегі функция мен орындарына қатарлар (3.11) мен (3.13) қойсақ және белісіз ескеріп мына теңдеуді аламыз:

(3.14)

ортогоналдық және толық болғандықтан. Бастапқы шарттар (3.10) шарттардан

(3.16)

теңдіктер орындалады.

Есептің (3.15)-(3.16) шешімі,

(3.17)

формуласымен анықталады.

Теңдіктен (3.17) табылған функцияны , (3.12) қатарға қойсақ, шекаралық есептің (3.10)-(3.11)-(3.3) шешімін аламыз.

Ескерту1. Шекаралық есепті (3.10)-(3.11)-(3.3) шешуді Дюамель қағидасын пайдаланып та шешуге болады. Ол үшін алдымен көмекші есеп қарастырайық:

, , , .

Егер де көмекші есептің шешімі болса, онда шекаралық есептің (3.10)-(3.11)-(3.3) шешімі келесі формуласымен анықталады:

(Тексеріңдер).

Ескерту 2. Егер де бастапқы шарттар (3.11) нөлдік емес болса,

, (3.18)

онда шекаралық есепті (3.10)-(3.18)-(3.3) екі есепке бөлуге болады.

есебі: ,

, ,

.

есебі: ,

, ,

.

Фурье әдісімен мен есептердің шешімдерін табу жолы жоғарыда көрсетілді. Егер де есептің шешімі , ал есебінің шешімі болса, онда қойылған(3.10)-(3.18)-(3.3) есептің шешімі,

болатынын тексеру қиын емес.

Фурье әдісімен жалпы түрде берілген шекаралық есепті шешу.

Есеп. Біртекті емес теңдеу (3.10).

Бастапқы шарттар (3.18) және шекаралық шарт,

(3.19)

қанағаттандыратын шешімін табу керек.

Фурье әдісін қолдану үшін шекаралық шарттар нөлге тең болуы керек. Шекаралық шартты (3.19) нөлдік шартқа келтіру үшін функция анықталған облыста және шекарада табу керек.

Егер де осындай табылса, онда белгісіз орнына жаңа белгісіз функция енгізіп белгісіз үшін щекаралық есеп:

(3.20)

, (3.21)

(3.22)

аламыз. Мұнда,

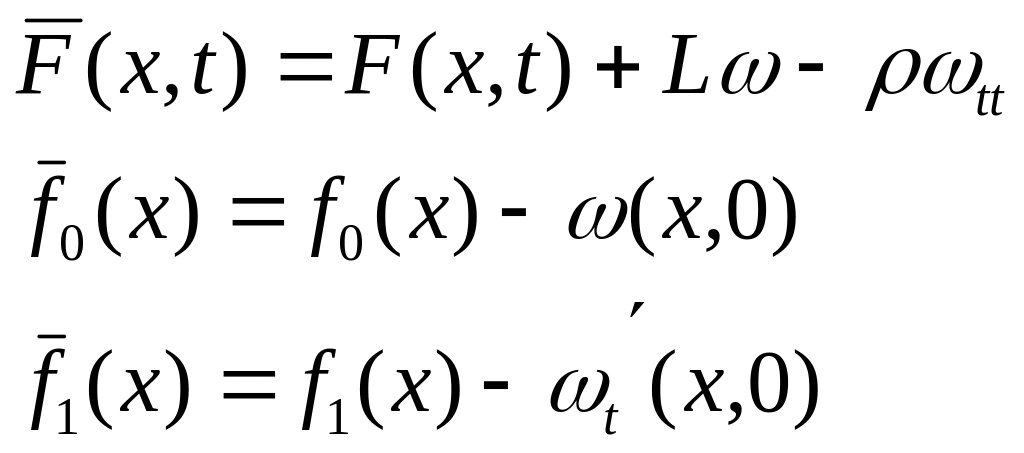
Алынған (3.20)-(3.21)-(3.22) есепті Фурье әдісімен шешуге болады. Фурье әдісімен (3.20)-(3.21)-(3.22) шекаралық есептің шешімі табылса, онда жалпы түрде берілген шекаралық есептің шешімі мына теңдікпен өрнектеледі:

.

Кезкелген облыс үшін (3.19) шекаралық шартты қанағаттандыратын функция оңай емес. Кейбір қарапайым шекаралық есептер үшін түрліше әдістер табуға болады.

3. Біртекті емес жылуөткізгіштік теңдеу үшін Коши есебі.

Есептің қойылымы жылуөткізгіш теңдеудің

аймақта, бастапқы шартты қанағаттандыратын,регулярлық шешімін табу керек.Ол үшін (1.1)-(1.2)есебін Дюамель әдісімен шығарамыз: (1.1)-(1.2)Есептерін 2–ке бөлеміз:А есебі: ;

Б есебі:

А есебінің шешімі

формуласы арқ жаз\ы.Б есебін Дюамель принципін қолдану арқ шығарамыз.Ол үшін В көмекші есебін қарастырамыз. .

Көмекші В есебін де Пуассон формуласы арқ өрнектеледі,

Дюамель принципі б\ша Б есебінің шешімін келесі формула арқ табамыз:

Сондықтан (1.1)-(1.2)Коши есебінің шешімі А мен Б есептерінің шешімінің қосындысы :

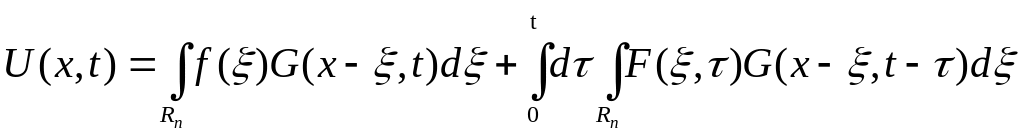
Формуласы арқылы табылады.

4. Жылуөткізгіштік теңдеу үшін экстремум қағидасы және оның қолданылуы.