6. Эйлер-Пуассон теңдеуі
Вариациялық есептер шеттері бекітілген және бекітілмеген есеп деп бөлінеді. Шеттері бекітілген есепті қарастырайық.
Берілген
(2.12)
функционалының
шекаралық шарттарын қанағаттандыратын
экстремумын табу керек. Мұндағы,
және
белгілі тұрақтылар. Әлсіз экстремумды
функциялар
класында іздейміз.
Есептің
геометриялық мағынасы: берілген
және
нүктелерін қосатын барлық
,
жатық қисықтарының арасынан
функционалына экстремум беретін қисықты
табу керек. Бұл есеп шеттері бекітілген
есеп немесе вариациялық есептеудің
қарапайым есебі деп аталады.
Ал
функционалы экстремум қабылдайтын
функциясы экстремаль деп аталады. Енді
функциясы
,
,
жиынында екі рет үздіксіз дифференциалданатын
фцнкция болсын деп ұйғарайық.
Егер
функциясы
өсімшесін алса, онда
функционалы қарастырылады. Мүмкін
болатын
өсімшелері
(2.13)
шарттарын
қанағаттандырсын. Шынында да, қисықтардың
шеттері бекітілген болғандықтан.
,
,
,
теңдіктерінен (2.12) шарттары орындалады.
Теорема
функциясы (2.12) шарттарды қанағаттандырып
және (2.12) функционалға экстремум берсе,
онда ол
(2.14)
Эйлер-Пуассон теңдеуінің шешімі болады.
Дәлелдеуі Берілген (2.12) функционалының бірінші вариациясының (2.4) формуласын пайдаланамыз, яғни,
Егер
функциясы (2.12) функциясына экстремум
беретін болса, онда экстремумның қажетті
шарты бойынша функционалдың вариациясы
нөлге тең болуы керек, яғни
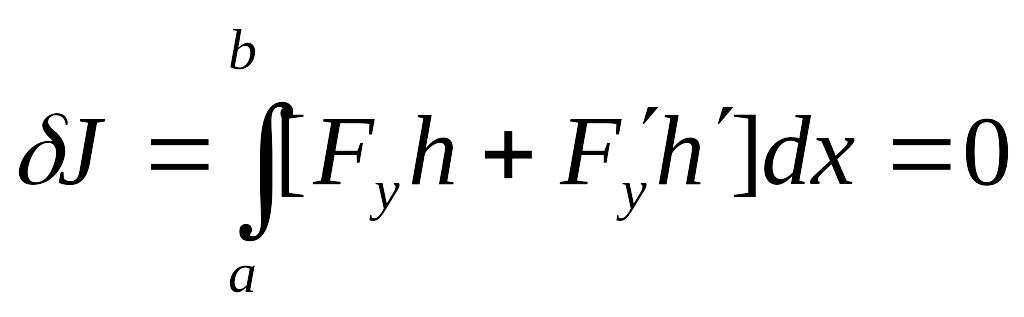(2.15)
Соңғы (2.15) өрнектегі екінші қосылғыштың интегралына бөліктеп интегралдау амалын қолданып және (2.13) шекаралық шарттарды пайдаланып, келесі теңдікті аламыз:
Осы
теңдікті (2.4) теңдеуге қойғанда
(2.16)
түріндегі теңдеу алынады.
Теңдіктің
сол жағындағы интеграл астындағы
функциясы
аралығында үздіксіз. Ал кез келген
функцясы осы аралықта үздіксіз және
(2.13) шекаралық шарттарды қанағаттандырады.
Олай болса, вариациялық есептеудің
негізгі леммасы бойынша
тепе-теңдігі алынады, яғни,
функциясы Эйлер-Пуассон теңдеуін
қанағаттандырады.
Эйлер-Пуассон теңдеуінің шешімі болатын функциялар экстремальдар деп аталады.
Егер
функциясы Эйлер-Пуассон теңдеуінің
шешімі болса, онда ол функцияның бірінші
вариациясының нөлге тепе-тең болғанымен
бірдей нәтиже. Сондықтан, бұл теңдеуді
қанағаттандыратын функцияларды
стационарлық функциялар деп атауға
болады еді. Бірақ та, вариациялық есептеу
теориясындағы әдет бойынша функционалдың
экстремальдары деп аталады.
7. Вариациялық есептеу. Қарапайым есеп. Әлді минимум. Әлсіз минимум. Функцинал өсімшесі.
Анықтама
1.1
Егер
жиынының әрбір
элементіне,
,
белгілі бір
саны
сәйкес келтірілсе, онда
жиынында
функционалы анықталған дейді.
Қарастырып
отырған
кеңістігінің
функционалының
аргументінің өсімшесі немесе вариациясы
деп
элементтерінің
айырымын айтады. Вариациялық есептерде
вариациясы
функциясын экстремумға зерттеу
есептеріндегі тәуелсіз айнымалының
өсімшесінің рөлін, ал функционал
вариациясы функцияның дифференциалының
рөлін атқарады. Ал
шамасын
өсімшесіне сәйкес функционал
өсімшесі
деп атайды. Алдын – ала
-ті
белгілеп алатын болсақ, онда
өсімшесі
-тің
функционалы болады. Өсімшені
қосындысы түрінде өрнектеуге болсын
деп ұйғарайық. Мұндағы,
функционалы
вариациясы бойынша сызықты, ал
шамасы
пен салыстырғанда жоғары ретті шексіз
аз шама. Осы
өсімшесінің басты
бойынша сызықты бөлігін
функционалының вариациясы деп атайды
және оны
деп белгілейді, яғни,
.
Әлсіз локәлдік минимумның қажетгі
шарттары әлді локәлдік минимумның да
қажетті шарттары болады.
Жай есеп. Мына есепті қарастырайық:
(3)
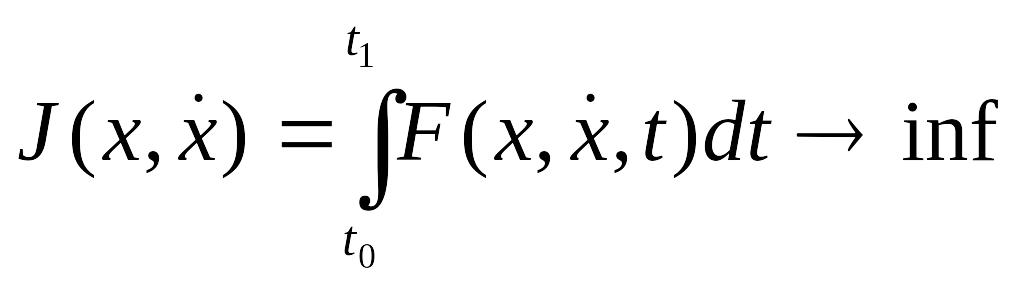
Функционалын
(4)
жиынында минимумдау керек.
1-анықтама.
Егер
орындалатын
кез
келген
ұйғарымды
функциясы
үшін
теңсіздігі
(мұндағы
)
орындалатын
саны
табылса,
онда
(5) (немесе
(3), (4)) есебіндегі
функционалын
функциясы
әлді
локәлдік
минимумге
жеткізеді
дейміз.
2-анықтама. Егер
(6)
орындалатын
кез
келген
ұйғарымды
функциясы
үшін
теңсіздігі
орындалатын
ε
>
0
саны
табылса
онда
(5)-(немесе
(3), (4)) есептегі
функционалын
функциясы
әлсіз
локәлдік
минимумге
жеткізеді
дейміз.