3. Сызықсыз программалау есебін шешу алгоритмі
Сызықсыз программалаудың келесі есебін шешудің тәртібін көрсетейік:
,
(1)
,
(2)
мұндағы
ал
- ашық,
дегі дөңес
жиынын қамтитын жиын, дербес жағдайда
алдыңғы лекциядағы (6)-(8) өрнектерінің
негізінде
.
1 . Әуелі
екендігіне көз жеткіземіз. Ол үшін
Вейерштрасстың теоремаларына сүйенеміз.
2. (1) - (2) есебі үшін жалпыланған Лагранж функциясын құрамыз
3.
,
(3)
(4)
(5)
шарттарынан
нүктелерін табамыз, мұндағы
-
берілген сан, дербес жагдайда
.
а) Егер
немесе
,
онда (4) шартын алмастырамыз:
.
(6)
Бұл жағдайда
түріндегі
белгісіздерді анықтауүшін ((3), (6), (5))
алгебралық теңдеулердің
жүйесін аламыз.
б) Егер алгебралық
теңдеулерді ((3), (5), (6)) немесе (3) - (5)
жүйелерін шешкен соң
болса, онда (1) - (2) есебі ерекшеленбеген
деп аталады. Ерекшеленбеген есептегі
(3) шартты неғұрлым қарапайым
шартымен алмастыруға болады. Егер
ерекшеленбеген есептегі
жұбы
Лагранж функциясының
қайқы нүктесі болса, онда
глобәлдік минимум нүктесі.
4. Сызықсыз программалаудың келесі есебін қарастырайық
(7)
(8)
Бұл (7), (8) есебі
(1)-(2) есебінің дербес жағдайы.
.
Егер
векторлары сызықты тәуелсіз болса, онда
(7) - (8) есебіндегі
нүктесі қалыпты минимум нүктесі делінеді.
Ескерту: егер
қалыпты нүкте болса, онда (7) - (8) есебі
ерекшеленбеген есеп болғаны. Шынында
да (7) - (8) есебі үшін
(9)
тендігі орындалады.
Егер мұндағы
,
онда
векторларының
сызықты тәуелсіздігінен алатынымыз:
.
Сонда
.
Бұл (З)-ке қайшы.
(7)- (8) есебінің
қалыпты нүктесі делік. Онда
деуге болады да Лагранж функциясы
түрінде
өрнектеледі.
4.Түйіндестік теориясы
5. Сызықтық программалаут есебін шешу. Симплекc әдісі
Канондық түрдегі сызықты программалау есебін қарастырайық:
(1)
мұндағы
-
берілген векторлар, А- берілген
ретті матрица.
матрицасын
түрінде жазуға
болады. Мұндағы
векторы шарттар векторлары деп, ал
- шектеулер векторлары деп аталады. Енді
теңдеуі
түрінде жазылады. Мына
,
жиындары аффиндік жиындар, яғни дөңес,
онда (1) - есеп дөңес программалау
есебі болып шығады.
Симплекс-әдіс.
Тұңғыш рет (1) - есептің шешімі
симплексінде қарастырылғандықтан
сызықты программалаудың мұндай есептерін
шешу әдісі симплекс әдіс деп аталды.
1 анықтама.
Егер
нүктесі
түрінде өрнектелмейтін болса, онда ол шеткі (немесе бұрыштық) нүкте деп аталады.
Осы анықтамадан шеткі нүкте U жиынындағы ешбір кесіндінің ішкі нүктесі болмайтындығын көреміз.
1 Лемма.
Шеткі нүктенің
оң координаттарының саны m
- нен аспайды.
2 Лемма. Шеткі нүктенің оң координаттарына сай шарттар векторлары сызықты тәуелсіз.
2-анықтама.
Егер ұйғарымды векторлардың оң
координаттарының саны А матрицасының
рангынан кем болмаса (яғни
,
тендеуіндегі нөлден ерекше қосылғыштар
А матрицасының рангынан кем болмаса),
онда (1) -түрдегі есеп сызықты программалаудың
канондық түрдегі ерекшеленбеген есебі
деп аталады.
3-лемма.
Айталық
.
Егер ерекшеленбеген есептегі ұйғарымды
векторының дәл m
оң координаты болса, онда u
- U жиынындағы шеткі нүкте.
Дәлелі.
Мәселен
ұйғарымды векторы дәл m
оң координатқа ие болсын делік. Сонда
u
- U жиынындағы шеткі нүкте екендігін
көрсетейік.
Қарсы жориық:
(
нүктесі шеткі нүкте емес болатын)
саны мен
нүктелері табылсын дейік. Бұл өрнектен
шығатыны:
Айталық:
.
Демек
.
Байкайтыныныз:
кез келген
кезінде
.
Мәселен,
векторының алғашқы m
координаттарының ішінде терістері де
бар болсын дейік. Онда
ды 0-ден
дейін ұлғайтып,
векторының алғашқы m
координаттарының бірі оң, ал қалғандары
теріс болатын
санын табамыз. Дәл осылай, егер
онда
ды 0 ден
ке дейін азайтып, кайшылыққа ұрынамыз.
Лемма дәлелденді.
Ескерту: егер
онда сызықты программалаудың (1) есебі
ерекшеленбеген деп кесіп айтуға болмайды.
4-лемма.
Кез келген
нүктесін U жиынындағы шеткі нүктелердің
дөңес сызықты комбинациясы ретінде
өрнектеуге болады, яғни
-
U жиынындағы шеткі нүктелер.
5-лемма.
U
-
дегі дөңес, шектелген, тұйық жиын делік,
яғни
.
Онда
функциясының U жиынындағы минимум U
жиынының шеткі нүктесінде болады. Егер
U -дың бірнеше шеткі нүктелерінде
U жиынындағы минимумына жетсе, онда
тап сол минимум мәніне кез келген
нүктелерінде жетеді.
Дәлелі.
Мәселен
нүктесінде U -дағы минимуміне жетсін.
Егер,
шеткі нүкте болса, онда лемма дәлелденді.
Айталық
- қандай да бір U
жиынындағы шекаралық немесе ішкі нүкте
болсын. Ендеше 4-леммадан
,
мұндағы
- U
жиынының шеткі нүктелері. Функция мәні
мұндағы
Мәселен
.
Онда
Осыдан
,
демек U -дағы
нүктесінде болады.
Мәселен
делік, мұндағы
- U жиынының шеткі нүктелері. Енді
екенін көрсетейік, мұндағы
.
Шынында да
.
Лемма дәлелденді.
Жоғарыдағы 4-5
леммалар шектелген дөңес түйық U жиыны
бар, (1)- түріндегі канондық формадағы
барлық сызықты программалау есебі ұшін
ақиқат екендігін байқаймыз. 1-5 леммалардан
көретініміз: канондық түрдегі сызықты
программалау есебін шығару алгоритмі
U жиынындағы бір шеткі нүктеден екінші
шеткі нүктеге көшуге негізделуі керек,
әрі көшкен кезде соңғы шеткі нүктедегі
функциясының мәні алдыңғы шеткі нүктедегі
мәнінен кем болуы керек. Мұндай алгоритм
(1) есеп шешімін санаулы қадамнан соң
алуға мүмкіндік береді, өйткені U
жиынының шеткі нүктелерінің саны
берілген
санынан аспайды (ақаусыз есеп жағдайында
).
Әрбір
шеткі нүктесінен
шеткі нүктесіне көшкен сайын, осы
шеткі нүктесі (1)-(2) есебінің шешімі
болатындығына көз жеткізу қажет. Ол
үшін әр нүктеде оңай тексерілетін
тиімдліктің жалпы баламасы болуы керек.
Төменде канондық формадағы ерекшеленбеген
сызықты программалау есебі үшін тиімділік
баламасы келтірілген.
Мәселен (1)-есеп
ерекшеленбеген және
нүктесі (1) есебінің шешімі дейік. Онда
5 леммаға орай,
нүктесі шеткі нүкте. Яғни (1)-есеп
ерекшеленбеген, ендеше
шеткі нүктесі дәл m
оң координатқа ие. Жалпылыққа нұқсан
келтірмей,
векторының алғашқы m
координаты оң деп санаймыз, яғни
векторы мен А матрицасын келесі түрде
өрнектейік:
мұндағы
2 - леммаға орай,
шеткі нүктесінің оң кординаттарына
сәйкес шарттар векторлары
-
сызықты төуелсіз, яғни
матрицасы айрықша емес, демек кері
матрицасы табылады.
6-лемма. (Тиімділік баламасы) шеткі нүктесі ерекшеленбеген канондық түрдегі (1), (2) сызықты программалау есебінің шешімі болуы үшін
(2)
шарты орындалуы қажетті және жеткілікті.
Дәлелі.
Қажеттілігі.
Мәселен
шеткі нүктесі ерекшеленбеген есептің
шешімі болсын делік, мұндағы
,
.
Айталық
,
мұндағы
- еркін нүкте.
нүктесіндегі ұйғарымды
бағыттар жиынын анықтайық. Ескерту:
барлық
кезінде
болатын
саны табылса, онда
векторы
нүктесіндегі ұйғарымды бағыт делінеді.
Вектор
түрінде
өрнектелсін, мұндағы
.
Мына
тиістілігінен
.
онда
демек, соңғы теңдіктен
.
Осыдан
.
Жеткілікті аз
кезінде
теңсіздігі орындалады, ендеше
нүктесіндегі ұйғарымды бағыттар
(3)
өрнегінен анықталады.
Сонымен, еркін
векторларын тандау арқылы табатынымыз
және әр элементі
түріндегі (яғни
)
ұйғарымды L
бағытын құрамыз. Енді кез келген
нүктесін
,
түрінде
жазамыз. Демек,
.
онда
нүктесінде
теңсіздігі орындалуы қажет (5 -лекция).
Осыдаы мынаны
ескерсек:
.
болғандықтан
.
Бұдан (2) - формуладағы
мәнін қойсақ
.
Осыдан (2) теңсіздігі шығады. Қажеттілік
дәлелденді.
Жеткіліктілігі.
Мәселен (2) теңсіздік орындалсын делік.
шеткі
нүкте екендігін көрсетейік.
функциясы дөңес U жиынындағы дөңес
функция, ендеше
теңсіздігі орындалуы қажетті және
жеткілікті. Осыдан, дербес жағдайда
,
алатынымыз
,
.
Онда
.
Демек,
нүктесінде U
–дағы
минимумына жетеміз. 5-леммаға орай,
- шеткі нүкте. Лемма дәлелденді.
Тиімділік баламасы
(2)
нүктесі үшін жасалған симплекс кесте
арқылы оңай тексеріледі.
Кестенің 1-бағанында
шеткі нүктесінең оң координаттарына
сәйкес шарттар векторы толтырылған.
Матрица
2-бағанда шеткі нүктенің оң координаттарына
сай
векторлары толтырылған: 3-бағанда шеткі
нұктенің тиісті оң координаттары
толтырылған ; келесі бағандарда
векторының
векторы бойынша
жіктелуі толтырылған; соңғы бағанда
мағынасы келесі лекцияда ұғындырылатын
мәндері толтырылған; сонғы екі жатық
жолдағы мәндері жете қарастырайық
векторлары сызықты тәуелсіз (2-лемма),
ендеше_олар
евклид
кеңістігінде базис құрайды, яғни кез
келген
векторын берілген жалғыз базис бойынша
жіктеуге болады. Симплекс кесте
-
Базис
C
…
…
…
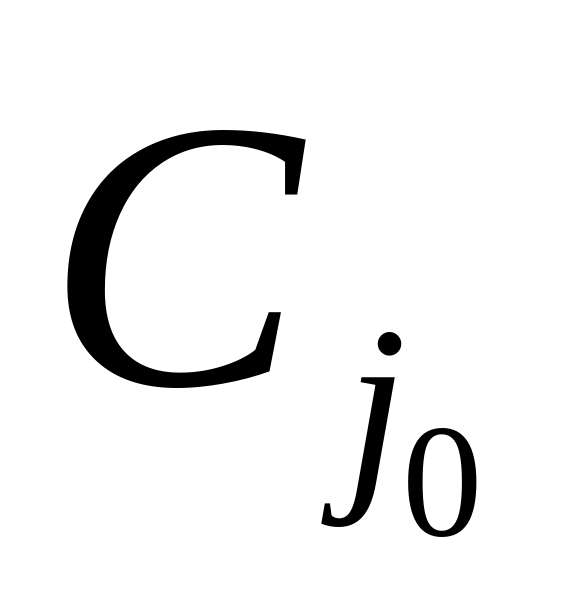
b
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
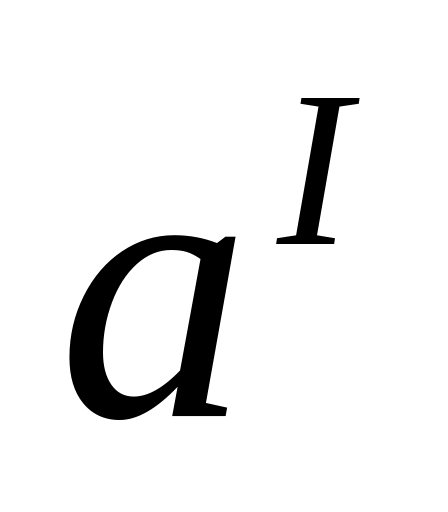
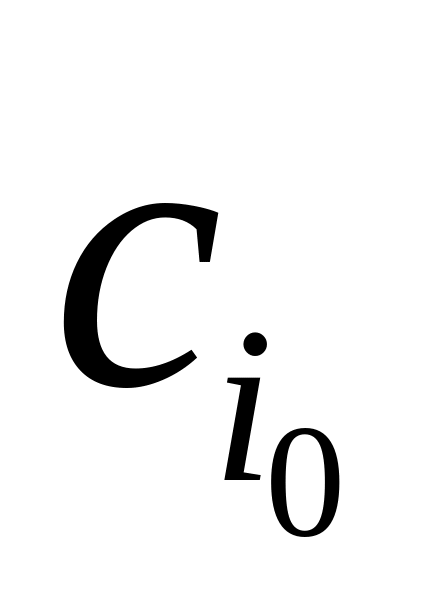
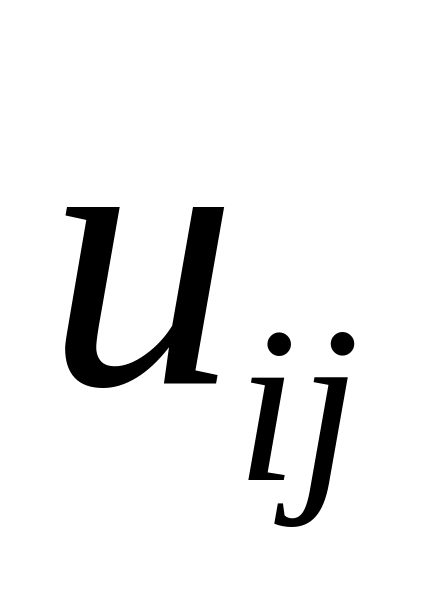
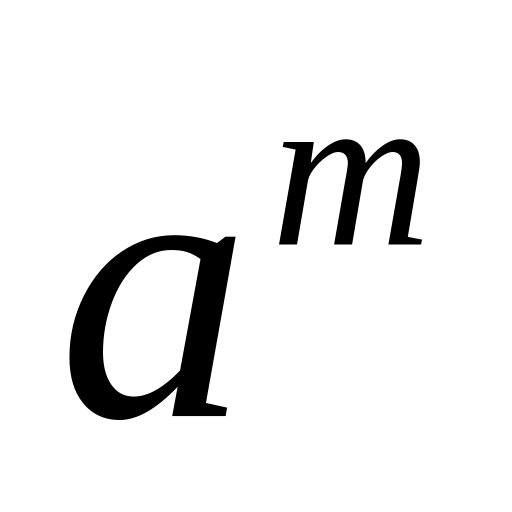
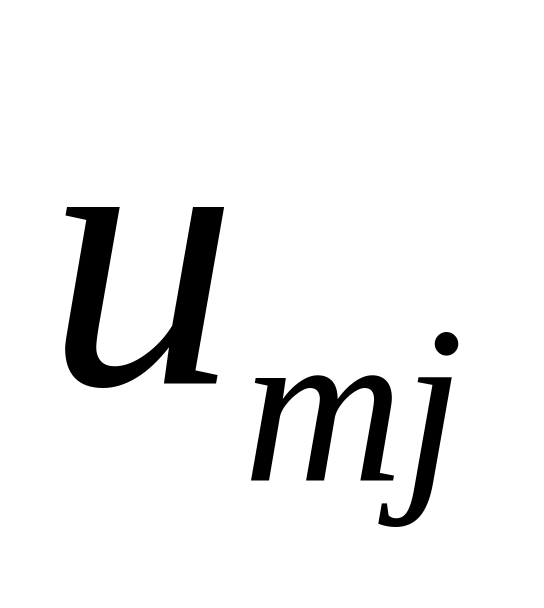
z
…
…
…
0
…
…
…
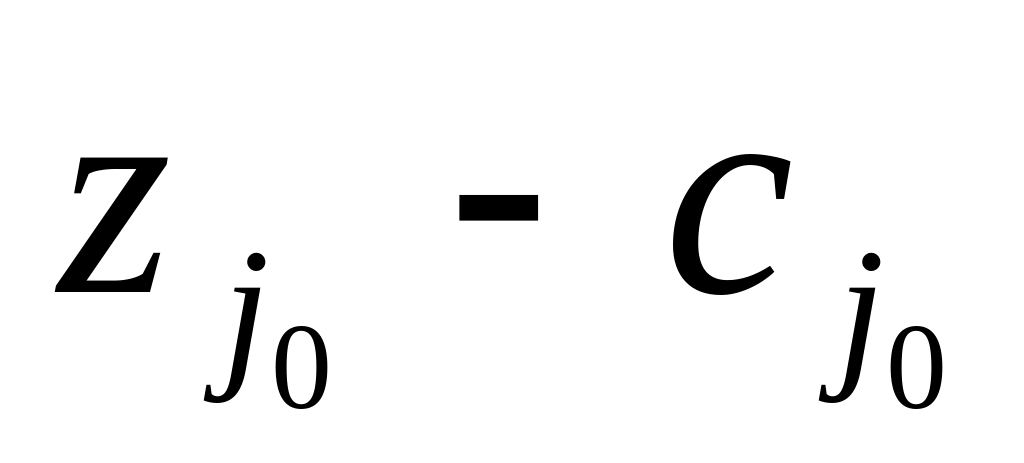
Демек,
Осыдан
.
Белгілеу енгізейік:
.
Аңғаратынымыз:
өйткені
.
Онда
,
мұндағы
Ал
болғандықтан
.
Демек,
.
Осы
өрнекті
тиімділік
баламасымен
(2) салыстырсақ
шеткі
нүктесі
есептің
шешімі
болуы
үшін
мына
болуы
қажетті
және
жеткілікті.
Сонымен симплекс кестенің соңғы жолының таңбасына қарап нүктесінің (1),(2) есебінің шешімі болатынын немесе болмайтынын анықтаймыз.