80)Голоморфты функция нөлдері және олардың реттері. Голоморыфты функцияның жалғыздығы туралы теорема.

Анықтама. Егер функциясы нүкте маңайында дәрежелік қатарға жіктелсе, онда нүктесінде голоморфты функция деп аталады.

дің жинақталу радиусы. -нің қосындысы функциясы жинақталу дөңгелегінде аналитикалық функция.

Функция голоморфтығы оның сол нүкте маңайында аналитикалық болуымен эквивалентті. Себебі, егер функция нүктесінде гoломорфты болса, онда болатын дөңгелек табылады және бұл дөңгелекте дәрежелік қатар. бойынша жіктеледі. функциясы дәрежелік қатар қосындысы ретінде нүктеде аналитикалық функция болады, және керісінше, егер аналитикалық функция болса, онда оны дәрежелік қатарға жіктеуге болады, яғни голоморфтық болады.

Анықтама. aналитикалық функциясының облысында нөлі деп, теңдеуін қанағаттандыратын нүктені айтады.

функциясы облысында гломорфты функция болады және нүктеде нөлге тең

-дың барлық, коэффиценттері бірдей тең0(нөл) бола алмайды. Олардың ішінде нөлге тең емес коэффицентті бар салардың ішіндегі ең кішісін арқылы белгілейміз.

нүктесі функциясы –ші ретті нөлі деп аталады.

Егер болса, онда нөлді қарапайым нөл деп атайды. Ал нөлді еселі нөл деп атайды.

Голоморфты функцияның жалғыздығы.

Теорема.Голоморфты функция дәрежелік қатарға жіктеледі.

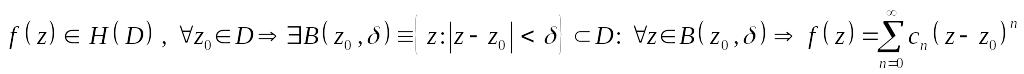
және осы жіктеу жалғыз.

Дәлелдеу: Айталық, дөңгелегінде функциясы мынадай түрде жіктелсін. _{және бізге екенін көрсету керек. тура сол сияқты . Ары қарай индукция бойынша дәлелденеді.}

81)Аналитикалық жалғастыру: аналитикалық жалғастыру принципі.Аналитикалық функция дегеніміз облыстаың кез келген нүктесінде ақырлы туындысы бар функция. Егер функциясының бірінші ретті туындысы бар болса, онда оның осы облыста барлық ретті туындыоары бар және олар аналитикалық функция.

Аналитикалық жалғастыру. Айталық, келесі шарттар орындалсын:

1. функциясы жиынында анықталған.

2. функциясы жиынын қамтитын облысында регулярлы болсын.

3. Егер болғанда, онда функциясы функциясының аналитикалық жалғастыруы болады.( жиынынан облысына). Аналитикалық жалғастырудың маңызды қасиеттерінің бірі оның жалғыздығы.

Теорема.(Аналитикалық жалғастыру принципі). Айталық, жиынының облысында тиісті шектік нүктесі болсын. Онда жиынынан облысына аналитикалық жалғастыру жалғыз болады.

Дәлелдеу: Aйталыық, жиынында анықталған функциясының облысында екі аналитикалық жалғастыру болсын: Eгер үшін болғандықтан, онда жалғыздық теоремасы бойынша облысында болу керек. Дербес жағдайда егер облысында жатқан қисық болса немесе облысының ішкі облысы болса, онда функциясының облысында бірден көп аналитикалық жалғастыруы болмайды.

Мысалы. функциясының аналитикалықжалғастыруын табайық. Бұл қатар шеңберінде жинақталады және регулярлы функция болады. функциясы облысында регулярлы (бұл комплекс жазықтықтың кеңейуі, нүктесін алмағанда) және егер болғанда . Осылайша, функциясы функциясының жиынына облысына аналитикалық жалғастыруы (жалғыз) болып табылады.