76.Кешен сандар өрісі. Кешен санның нақты және жорамал бөлігі, модулі мен аргументі.

Натурал сандар белгілі бір заттарды санау үшін қажет болды. теңдеуінің натурал сандар жиынында шешімі жоқ. Сондықтан да, оны кеңейту қажеттігі туындады. Осылай бүтін сандар жиыны пайда болды. теңдеуінін бүтін сандар жиынында шешімі жоқ, сондықтан оны да кеңейту қажет болды. Осыдан рационал сандар жиыны пайда болды. теңдеуінің рационал сандар жиынында шешімі жоқ, сондықтан нақты сандар жиыны пайда болды. теңдеуі нақты сандар жиынында шешімі жоқ, оны да кеңейту қажеттігі туындады, сондықтан да комплекс сандар жиыны пайда болды.1778 жылы Эйлер санын арқылы белгіледі. Ал комплекс сан дегенді Карно енгізді.

Теорема 1. 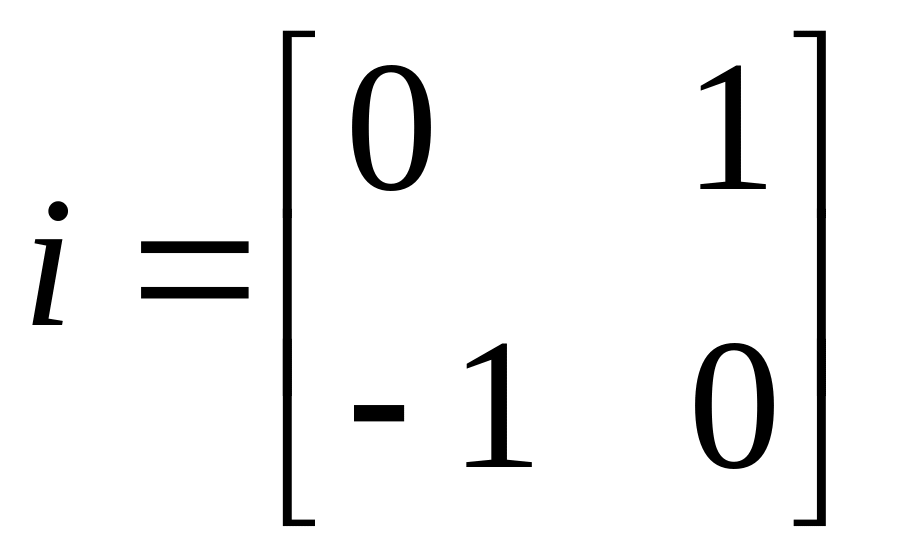матрицасы матрицалық теңдеуін қанағаттандырады.

Дәлелдеуі матрицалық қатынасының тікелей тексерісі арқылы қорытындылайды, яғни

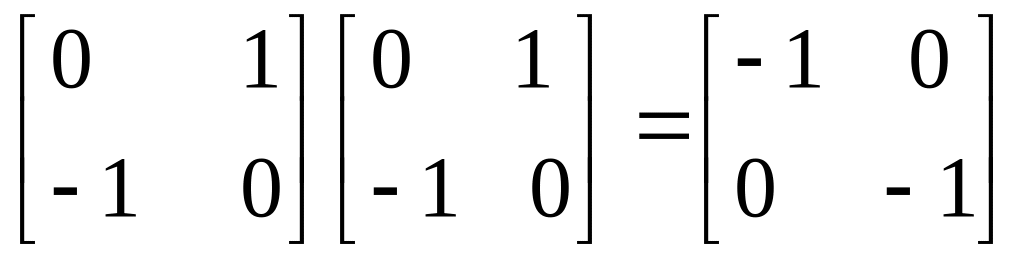
Арнайы матрицалар жиынын келтірейік

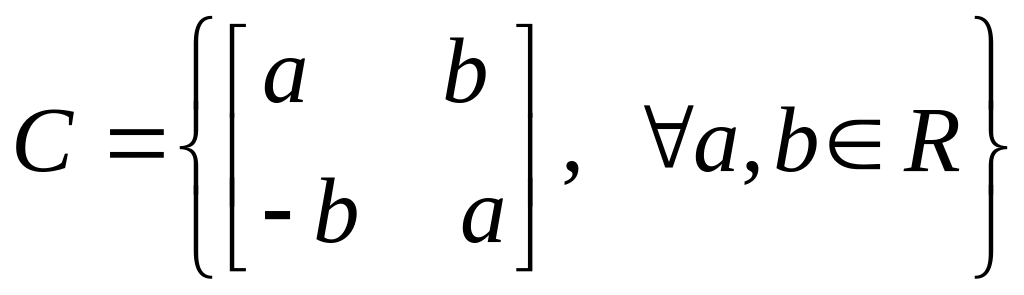
Теорема 2. С жиыны М жиынының және матрицасының кеңейуі болып табылады.

Дәлелдеуі . Егер b=0 болғанда, онда 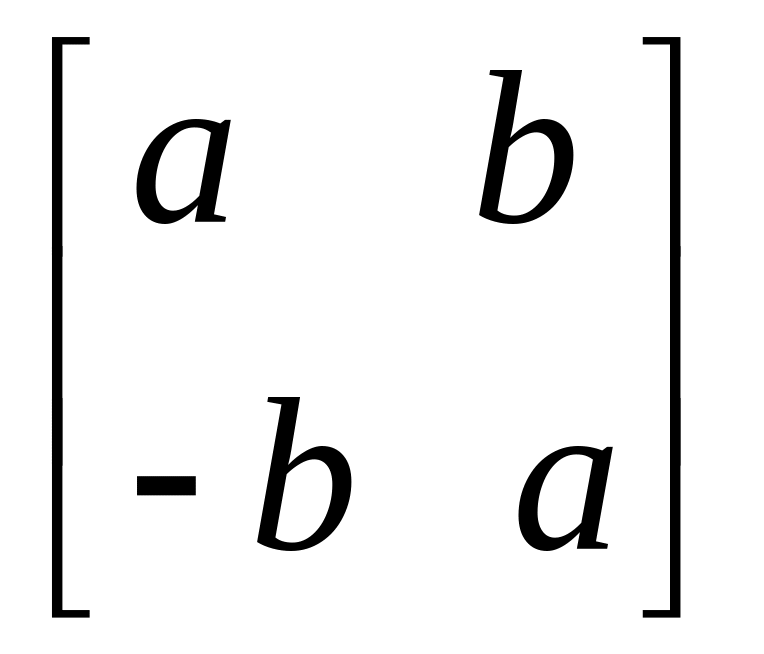түріндегі матрица М жиынына тиісті. Егер b=1, a=0 болса, онда түріндегі матрица i матрицасымен беттеседі.

Комплекс санның алгебралық түрі. Алдағы уақытта жоғарыда келтірілген матрицаны төмендегідей екі бекітілген матрицаны сызықтық комбинациясы түрінде өрнектеген қолайлы

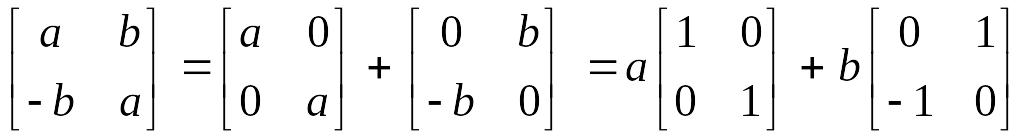
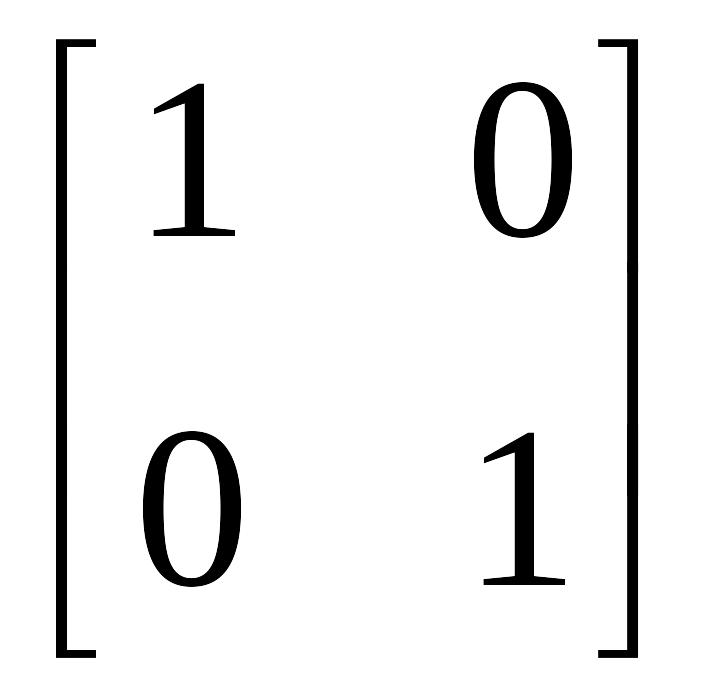бірлік матрицасы жиынына тиісті, сондықтан 1 нақты санына сәйкес келеді және оны жай ғана бірлік деп атаймыз. Екінші 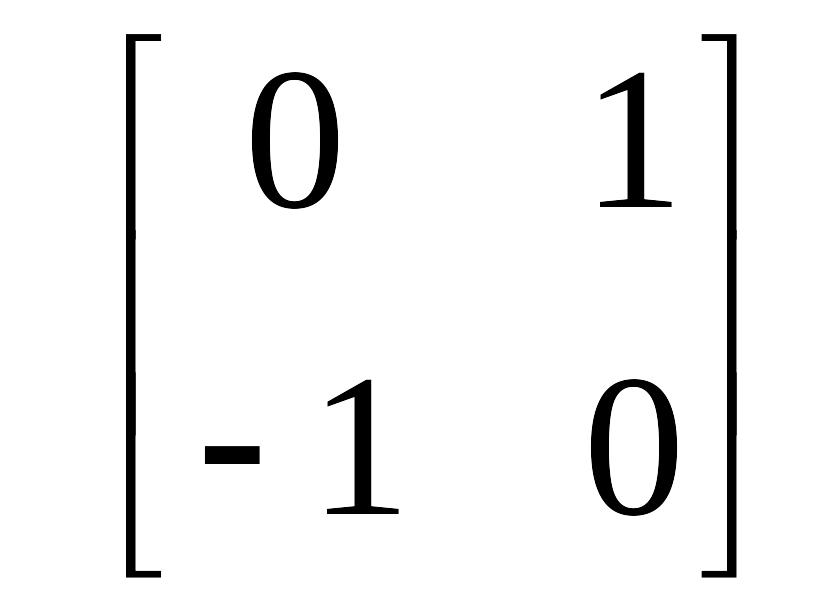матрицасы матрицасымен беттеседі, алдағы уақытта жорамал бірлік деп атаймыз. Сонымен келесі орынды:

Тұжырым. Кез келген комплекс сан бірлік және жорамал бірліктің сызықтық комбинациясын бола алады, яғни комплекс сан мына түрде жазылады: . Сызықтық комбинация коэффициенттері нақты сандар. Осылайша комплекс саннық алгебралық түріна аламыз.

Комплекс санның тригонометриялық түрі.

Бізге жұбы жазықтықта вектор бола алатыны белгілі.

Полярлық координаттар жүйесінде комплекс саны түрде жазылады, мұндағы - векторының ұзындығы, - векторының бағытына сәйкес бұрышы. шамасы модулі деп аталады, бұрышы аргументі деп аталады және сәйкесінше және белгіленеді.

Комплекс санның көрсеткіштік түрі.

Тұжырым 2 Жорамал бірлік дәрежесі тек төрт мәнді қабылдайды:

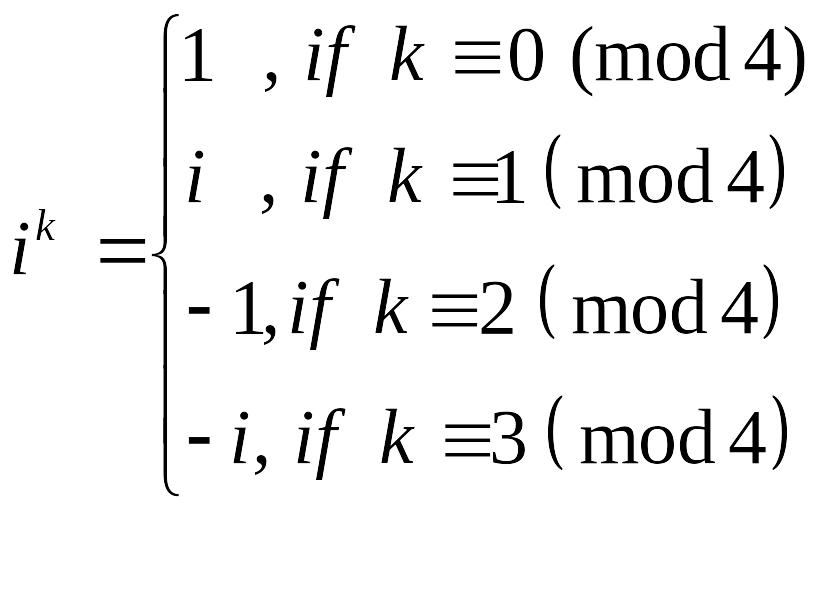
Тұжырым 3. үшін Тейлор қатары:

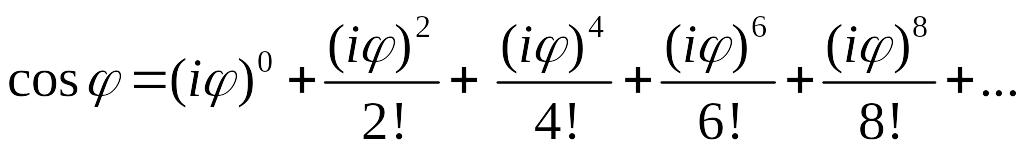
_{Дәлелдеу. Алдымен Тейлордың стандартты жіктелуін жазайық:}

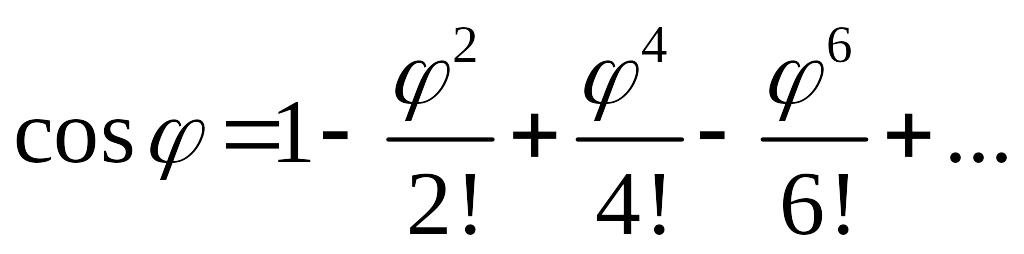
_{Тұжырым 2-ге сәйкес, жорамал бірліктің жұп дәрежелері кезектесіп} +1 және -1. Нәтижесінде 3 тұжырымын аламыз.

Тұжырым 4. үшін Тейлор қатары:

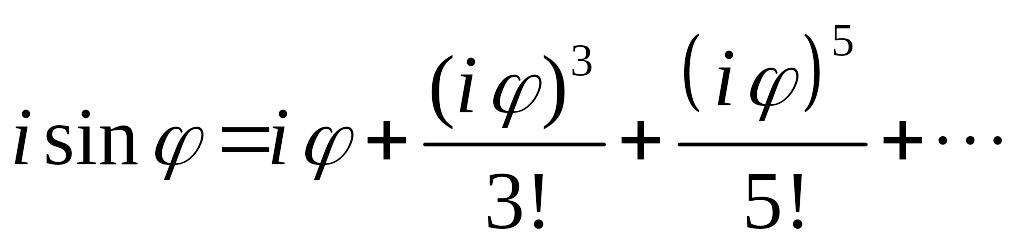
Теорема. Жорамал аргументті экспоненттік функция тригонометриялық функцияларының сызықтық комбинациялары бола алады, яғни барлық нақты үшін теңдігі орынды.

Дәлелдеуі. 3 тұжырымы бойынша мына қатынасты аламыз:

4 тұжырымнан келесі теңдік шығады: Енді оң бөліктерін қосу ғана қалады. Жоғарадағы теорема бойынша, комплекс санының экспоненттік түрін аламыз: , - комплекс сан модулі ал - аргументі.

77. Кешен айнымалы дифференциалданатын және голоморфты функциялар. Коши-Риман шарты.

Анықтама-1: Айталық кешен айнымалысы қайсыбір D облысында өзгеретін болсын. Егер айнымаласының әрбір мәніне өзге кешен айнымалысының бір немесе бірнеше мәндері сәйкес қойылса, онда кешен айнымалысын облысында анықталған -ке тәуелді кешен айнымалы функция деп атайды және оны арқылы белгілейді. Егер мұнда әрбір мәніне тек бір ғана кешен айнымалысы сәйкес қойылса, онда функциясын бірмәнді функция деп, ал егер әрбір мәніне екі немесе одан да көп кешен айнымалылары сәйкес қойылса, онда функциясын көпмәнді функция деп атайды.

Егер айнымалысы кешен айнымалысына тәуелді функция болса, онда және айнымалылардың әрқайсысы және -ке тәуелді функциялар болады: . Сонда , . Керісінше, теңдігіндегі функцияларының әрқайсысы және -ке тәуелді нақты айнымалы функциялар болса, онда айнымалысын кешен айнымалысына тәуелді функция деп санауға болады ( ).

Анықтама-2: Айталық функциясы с нүктесі маңында анықталған (фукнция осы с нүктесінде анықталмауы да мүмкін) болсын. Егер кез келген e>0 саны үшін d>0 саны табылып, теңсіздігін қанағаттандыратын әрбір үшін теңсіздігі орындалса, онда A санын функцияның болғандағы шегі деп атайды және оны былай белгілейді:

Анықтама-3: Айталық функциясы нүктесінде және оның маңында анықталған болсын. Егер

теңдігі орындалса, онда функцияны нүктесінде үздіксіз деп атайды. Егер функция D облысының әрбір нүктесінде үздіксіз болса, онда функцияны осы D облысында үдздіксіз деп атайды.

Анықтама: (Кешен айнымалы туынды). Айталық функциясы z₀ нүктесінің қайсыбір аймағында анықталған болсын. Егер шегі бар болса, онда функцияны z₀ нүктесінде дифференциалданады деп, ал осы шек мәнін функциясының z₀ нүктесіндегі туындысы деп атайды және оны f¢(z₀) арқылы белгілейді:

(1)

Анықтама: Егер функциясың D облысының әрбір нүктесінде үздіксіз туындысы бар болса, онда функцияны осы D облысында аналитикалық функция деп атайды.

Анықтама. Комплекс айнымалысы мағынасында туындысы бар функция голоморфты функция деп аталады.

функциясының z₀ нүктесіндегі туындысы:

_.

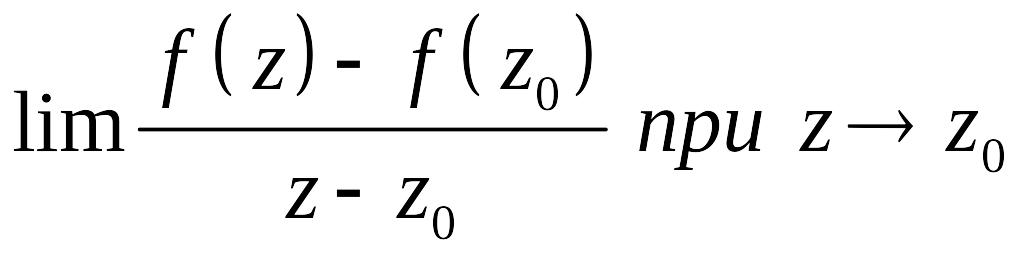Айталық, функциясы анықталу облысының ішкі нүктесінде голоморфты болсын.Бұл

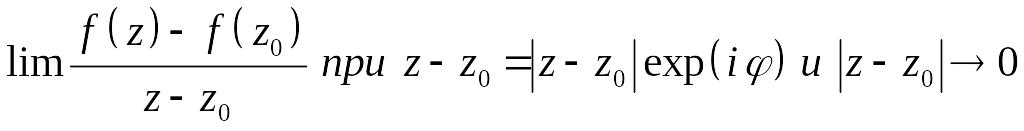
шегінің бұрышына тәуелді емес екендігін білдіреді. Берілген шектерді және 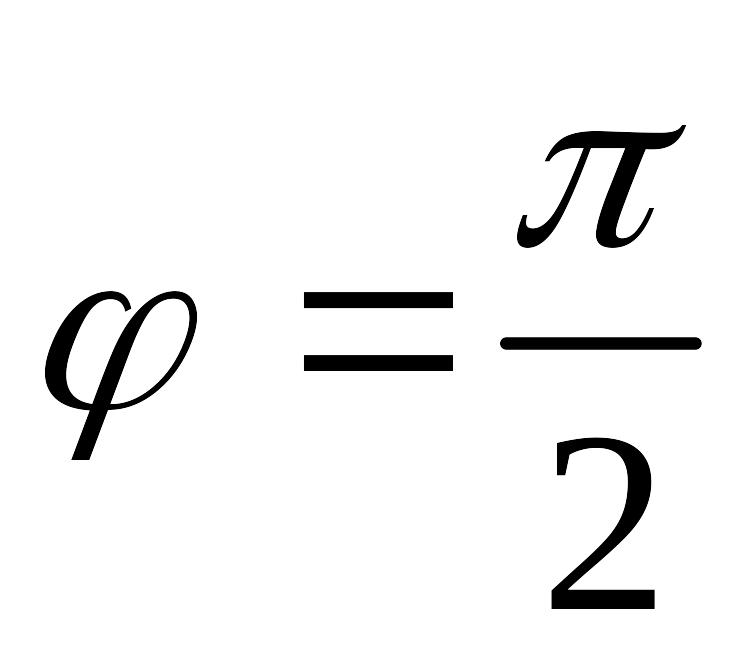болғанда салыстырайық:

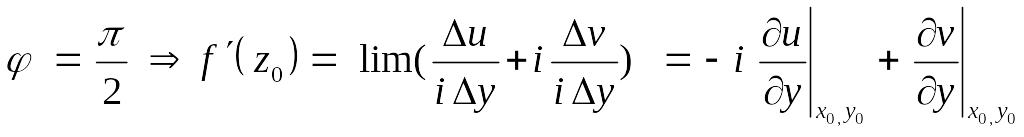
мұндағы . Бұдан шыққан функциялардың нақты және жорамал бөліктің дербес туындылары өзара тәуелді екенін көреміз, Яғни

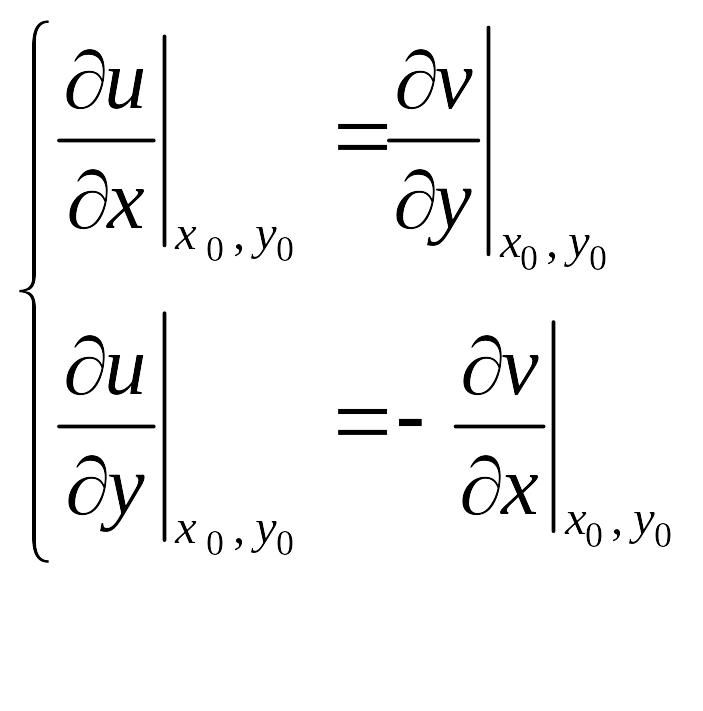
Бұл шартты Коши –Риман шарты деп атаймыз.