
1 Жинақы тізбек
1-
анықтама.
Егер
![]() санға белгілі бір ереже (заң) бойынша
санға белгілі бір ереже (заң) бойынша
![]() нақты саны сәйкестендірілсе, онда сан
тізбегі немесе жай тізбек берілген
дейді.
нақты саны сәйкестендірілсе, онда сан
тізбегі немесе жай тізбек берілген
дейді.
Тізбекті
![]()
![]()
![]()
![]() символдарының
біреуімен белгілейді.
символдарының
біреуімен белгілейді.
2-
анықтама.
Егер кез келген
![]() санына сәйкес N=N(
санына сәйкес N=N(![]() )
саны табылып,
)
саны табылып,
![]() үшін
үшін
![]()
теңсіздігі
орындалса, а санын
![]() тізбегінің шегі деп атайды да оны былай
жазады:
тізбегінің шегі деп атайды да оны былай
жазады:
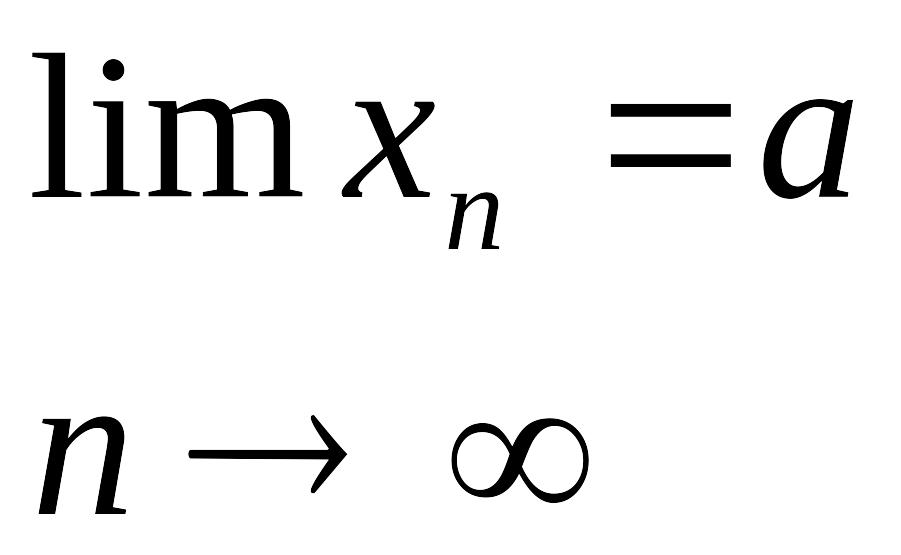
3-
анықтама.
Егер тізбек шегі
![]() саны тиянақты (шекті) сан болса, онда
оны а санына жинақты дейді.
саны тиянақты (шекті) сан болса, онда
оны а санына жинақты дейді.
1-теорема. Жинақты тізбектің тек бір ғана шегі бар.
яғни
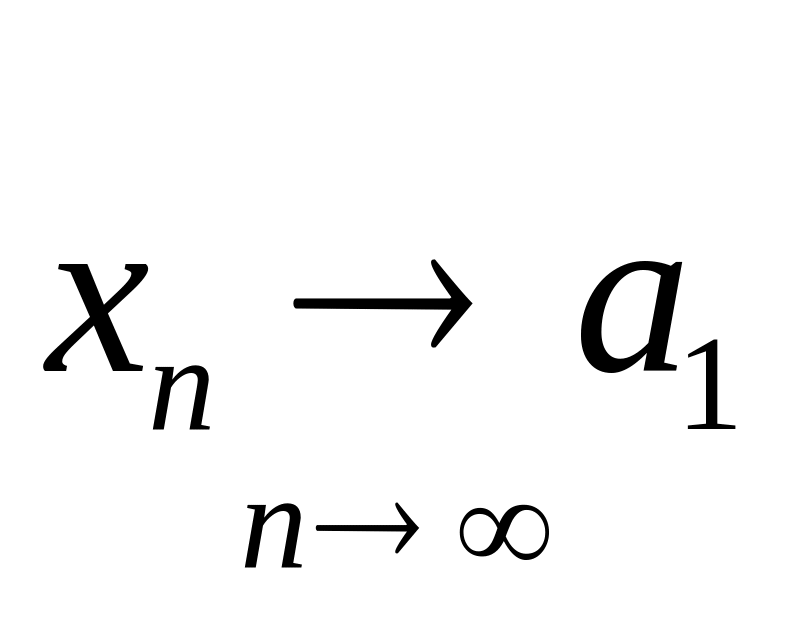
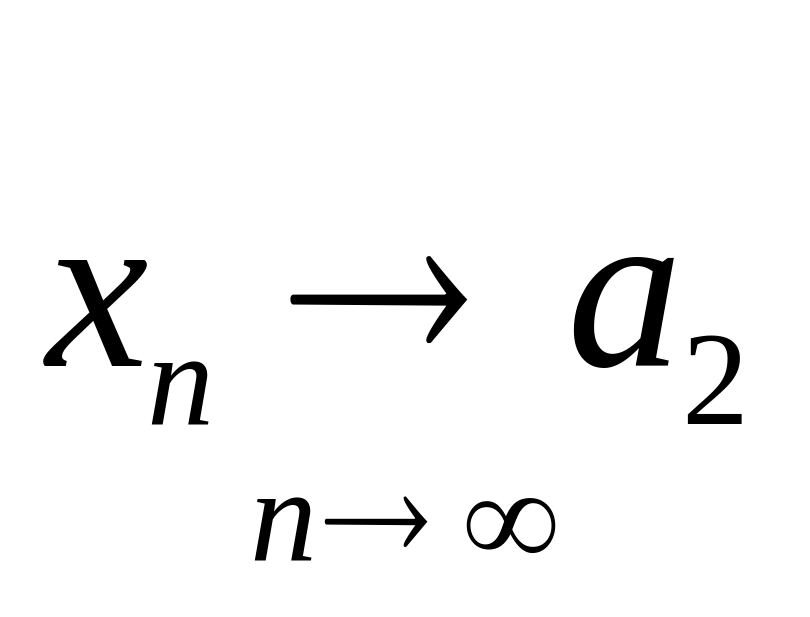

Д-уі:
:
![]()
:
![]() .
.
![]()
![]() ,яғни
,яғни
![]() Дәлелденді.
Дәлелденді.
2-теорема. Кез келген жинақты тізбек шектелген.
Ескерту. Кез келген шектелген тізбек жинақты деуге болмайды.
3
–теорема.
Егер {xn},
{yn}
тізбектері жинақты және
,
 болса, онда
болса, онда
{xn
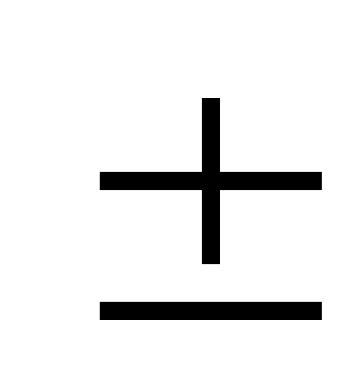 yn}
тізбегі жинақты,
lim(xn
yn)
= a
b.
yn}
тізбегі жинақты,
lim(xn
yn)
= a
b.
n![]()
{xn
 yn}
тізбегі
жинақты,
lim(xn
yn)
=
a
b.
yn}
тізбегі
жинақты,
lim(xn
yn)
=
a
b.
n
{
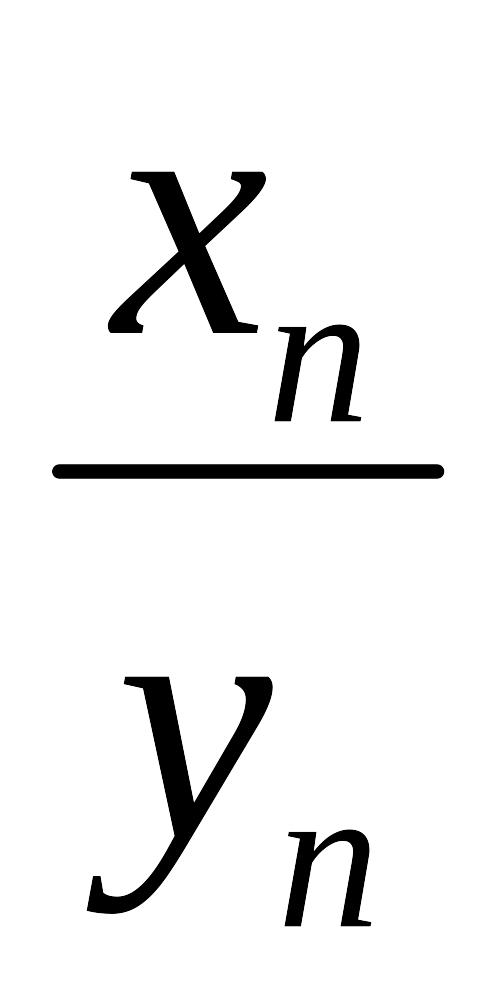 },
b
},
b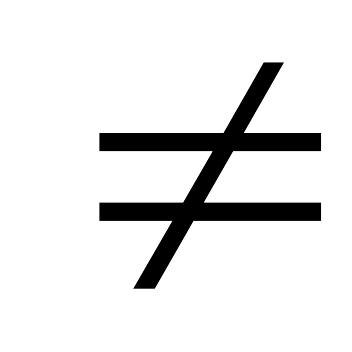 0
тізбегі
жинақты,
lim
=
0
тізбегі
жинақты,
lim
=
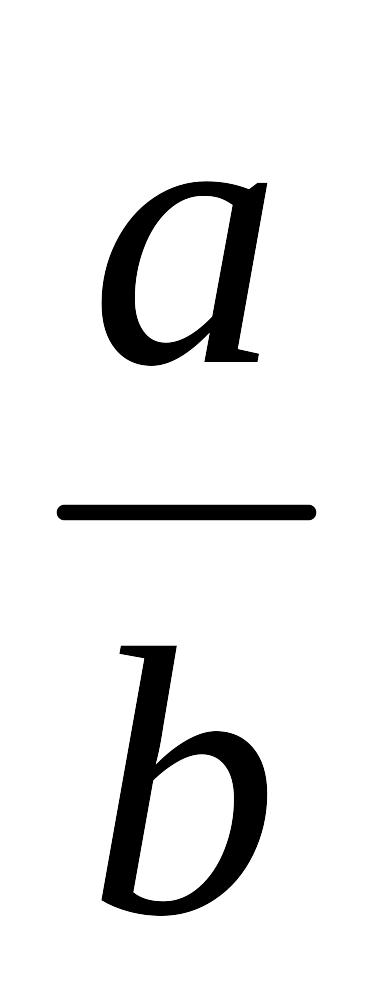
n
4
–теорема.
{xn},
{yn},
{zn}
үш тізбек үшін xn
![]() zn
yn
теңсіздігі
орындалса және lim xn=
a, lim yn=
b болса, онда lim zn=
a
zn
yn
теңсіздігі
орындалса және lim xn=
a, lim yn=
b болса, онда lim zn=
a
n n n
5.Егер
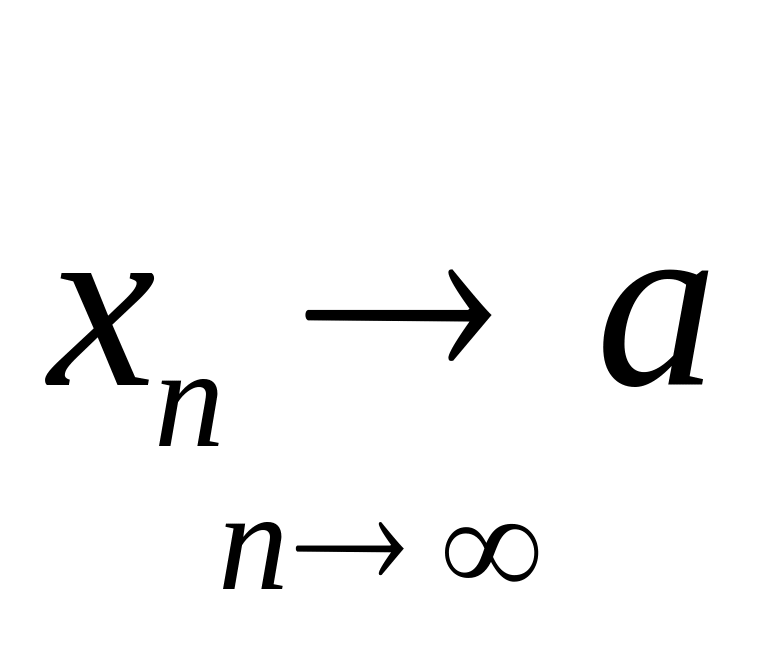
![]()
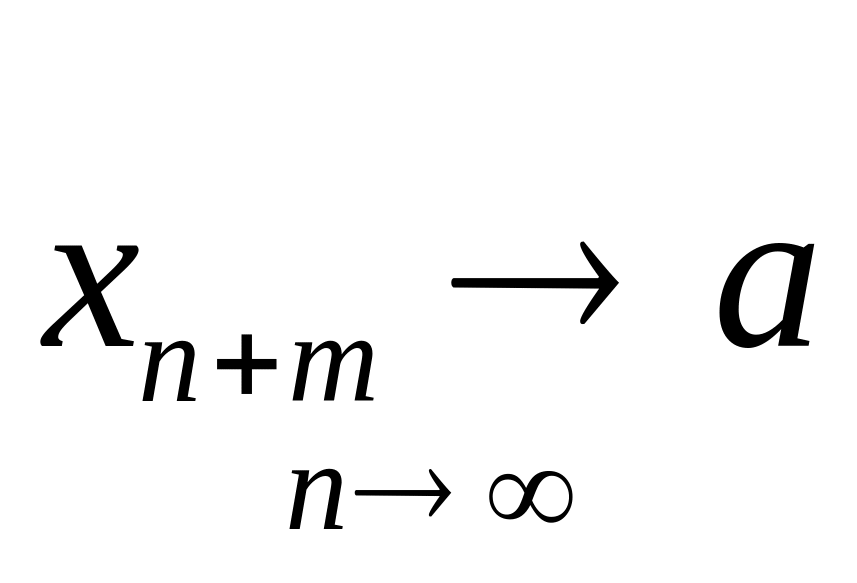
Д-уі:
дегеннің анықтамасы:
![]() онда келесі өрнек ақиқат
онда келесі өрнек ақиқат
![]()
![]() .
Дәлелденді.
.
Дәлелденді.
2 Tейлор
Айталық, f(x) функциясы [a,b] кесіндісінде n-1 - ретке дейінгі үзіліссіз туындысы бар болсын, ал (a,b) интервалында f(x) функциясының n –ші ретті туындысы бар болсын, онда [a,b] аралығындағы кез келген x0 және x үшін , осы екі нүктенің аралығында жататын ξ нүктесі бар болады және
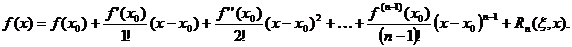 .
.
Төмендегі өрнекті
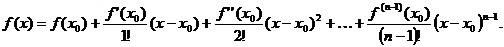
f(x) функциясы үшін x0 нүктесінің маңайындағы n-1 ретті Тейлор көпмүшелігі деп атаймыз.
Rn(ξ,x) өрнегі Тейлор формуласының қалдық мүшесі деп аталады.
Ескерту: егер х0 =0 болса, онда Тейлор формуласын кейде Маклорен формуласы деп атаймыз.
![]() ([a,b]
нақты
сандар жиынында анықталсын)
([a,b]
нақты
сандар жиынында анықталсын)
![]() (n-рет
туындысы бар болсын)
(n-рет
туындысы бар болсын)
![]() (n-ші
ретті туындысы үзіліссіз болса)
(n-ші
ретті туындысы үзіліссіз болса)
![]() (n+1
ретті туындысы бар болсын)
(n+1
ретті туындысы бар болсын)
![]()
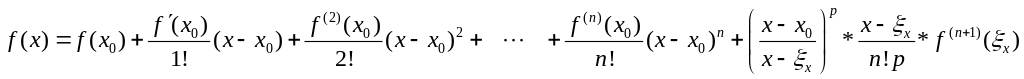
Д-уі:
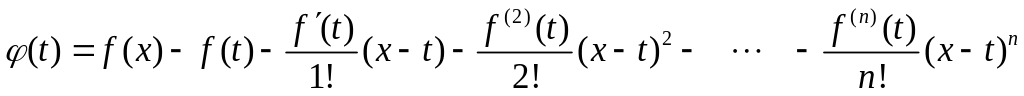
![]() аралығында
зерттейік.
аралығында
зерттейік.
![]()
![]() аралығында
дифференциалданады (туындысы
бар)
аралығында
дифференциалданады (туындысы
бар)


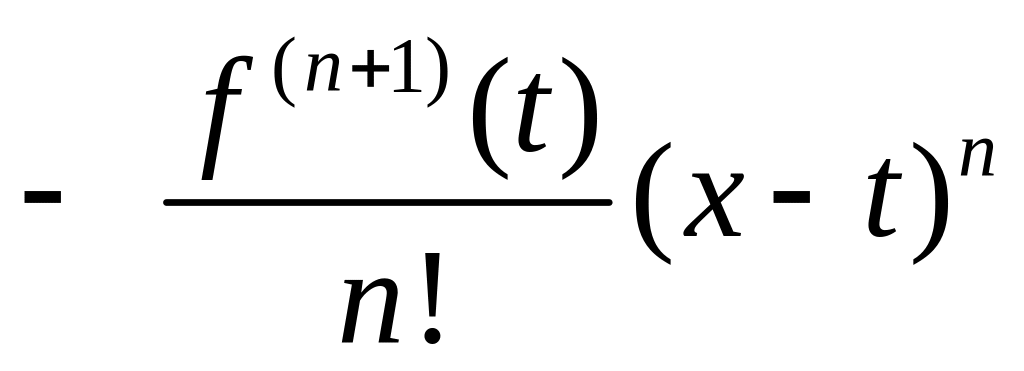 ,
,
яғни
![]()
![]() .
Енді Коши теоремасын қолдансақ.
.
Енді Коши теоремасын қолдансақ.
Коши теоремасы:
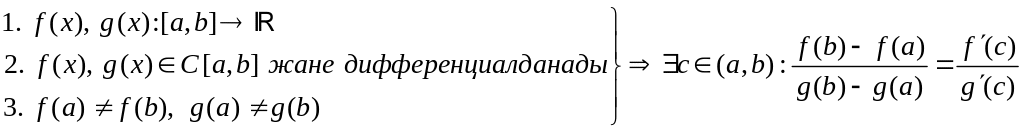
Осы Коши теоремасын қолдансақ.
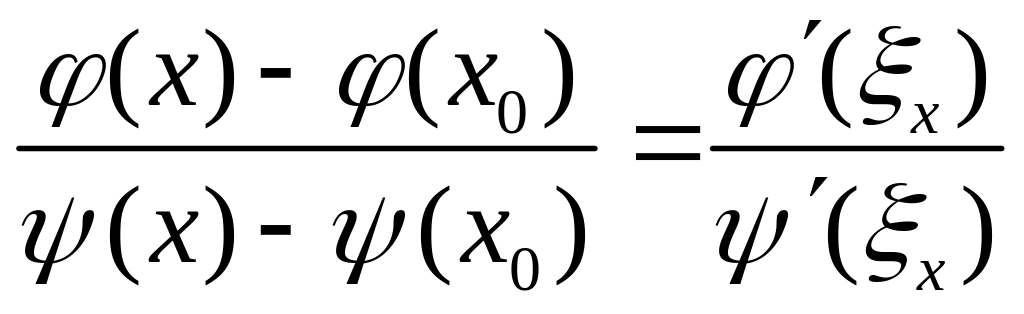
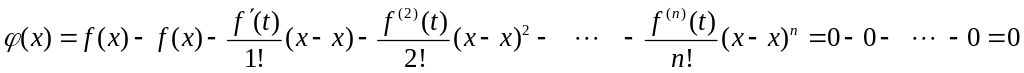
Яғни
![]()

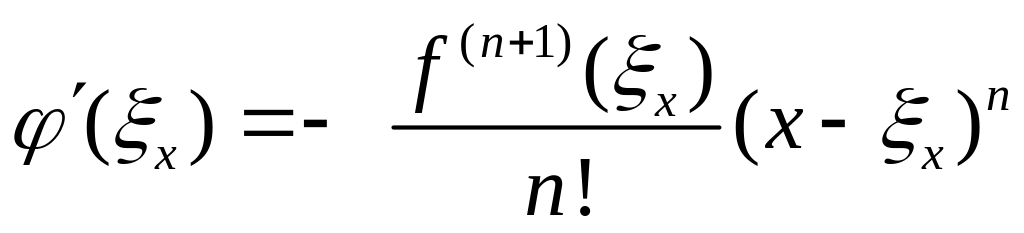
![]()
Яғни
![]()
![]()
![]()
Осы табылған мәндерді Коши теормасына қоямыз, сонда
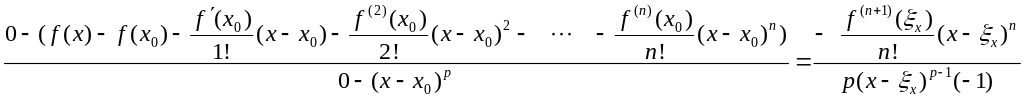
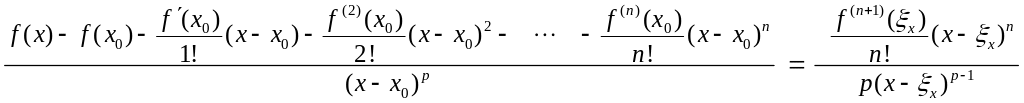
Дәлелденді.
3.Анықталған интегралдың орта мән теоремасы
Анықталған интеграл ертеректе жазық фигуралардың ауданын табу негізінде туындады. Ал қазір анықталған интеграл барлық техникалық ғылымдардағы аз шаманың үлкен сандарының қосындысын табуға арналған есептерді шешуде қолданылады.
Анықтама
1. Қисық
сызықты
трапеция деп ![]() жазықтығындағы
жазықтығындағы ![]() осімен,
осімен, ![]() және
және ![]() түзулерімен
шектелген облысты айтамыз,
мұндағы
түзулерімен
шектелген облысты айтамыз,
мұндағы ![]() және
және ![]() функциясының
графигі
функциясының
графигі ![]() аралығында
үзіліссіз .
аралығында
үзіліссіз .
Қарапайымдылық
үшін, ![]() деп
қарастыралық, яғни, қисық сызықты
трапеция
осінен
жоғары орналасқан. Бұл қисық сызықты
трапецияның ауданын жуық шамамен оны
мәндері
деп
қарастыралық, яғни, қисық сызықты
трапеция
осінен
жоғары орналасқан. Бұл қисық сызықты
трапецияның ауданын жуық шамамен оны
мәндері ![]() функциясының
кейбір таңдап алынған нүктелеріндегі
мәндерге тең болатын табаны мен
биіктіктері өте аз тік төртбұрыштардың
аудандарының қосындысымен алмастыру
көмегімен табуға болады.
функциясының
кейбір таңдап алынған нүктелеріндегі
мәндерге тең болатын табаны мен
биіктіктері өте аз тік төртбұрыштардың
аудандарының қосындысымен алмастыру
көмегімен табуға болады.
Анықтама
2. ![]() кесіндісін
тең
кесіндісін
тең ![]() бөлікке
бөлу деп осы кесіндіден алынған
бөлікке
бөлу деп осы кесіндіден алынған ![]() сандар
жиынтығын айтамыз, мұндағы
сандар
жиынтығын айтамыз, мұндағы ![]() және
және ![]() .
.
Әрбір
бөлік ![]() кесіндіден
қандай да бір
кесіндіден
қандай да бір ![]() нүктесін
аламыз, мұндағы
нүктесін
аламыз, мұндағы ![]()
Бұндай
бөліктеуді ![]() әрпімен,
ал әр бөліктің ұзындығын
әрпімен,
ал әр бөліктің ұзындығын ![]() арқылы
белгілейміз.
кесіндісінде
қандай да бір
арқылы
белгілейміз.
кесіндісінде
қандай да бір ![]() функциясы
анықталған болсын.
функциясы
анықталған болсын.
Анықтама
3.
функциясының
кесіндісін
бөліктеуден
тұрғызылған интегралдық
қосындысы деп ![]() таңдалынған
нүктесіндегі функцияның мәнінің бөліктің
ұзындығына көбейтінділерінің қосындысын
айтамыз.
таңдалынған
нүктесіндегі функцияның мәнінің бөліктің
ұзындығына көбейтінділерінің қосындысын
айтамыз.
Бұндай қосындыны былай белгілейміз:
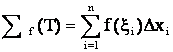 .
.
Егер
,
онда ![]() интегралдық
қосындысы табаны
интегралдық
қосындысы табаны ![]() және
биіктігі
және
биіктігі ![]() болатын
тік төртбұрыштардан тұратын
баспалдақты фигураның ауданына тең,
яғни,
қосындысы
жуық шамамен оған сәйкес қисық сызықты
трапецияның ауданына тең.
болатын
тік төртбұрыштардан тұратын
баспалдақты фигураның ауданына тең,
яғни,
қосындысы
жуық шамамен оған сәйкес қисық сызықты
трапецияның ауданына тең.
Анықтама 4. функциясының кесіндісіндегі анықталған интегралы деп осы функцияның кесіндісін бөліктеудегі интегралдық қосындыларының -дің максимал мәні нөлге ұмтылғандағы шегін айтамыз, яғни,
 .
.
Егер аралығында болса, онда бұл интеграл сәйкес қисық сызықты трапецияның тура ауданын өрнектейді.
Орта мән туралы бірінші теорема:

Д-уі
:
![]() ,
онда
,
онда
![]() ;
ал бізде
;
ал бізде
![]() оң функция болғандықтан келесі теңсіздік
орынды:
оң функция болғандықтан келесі теңсіздік
орынды:
 осы
теңсіздікті
осы
теңсіздікті
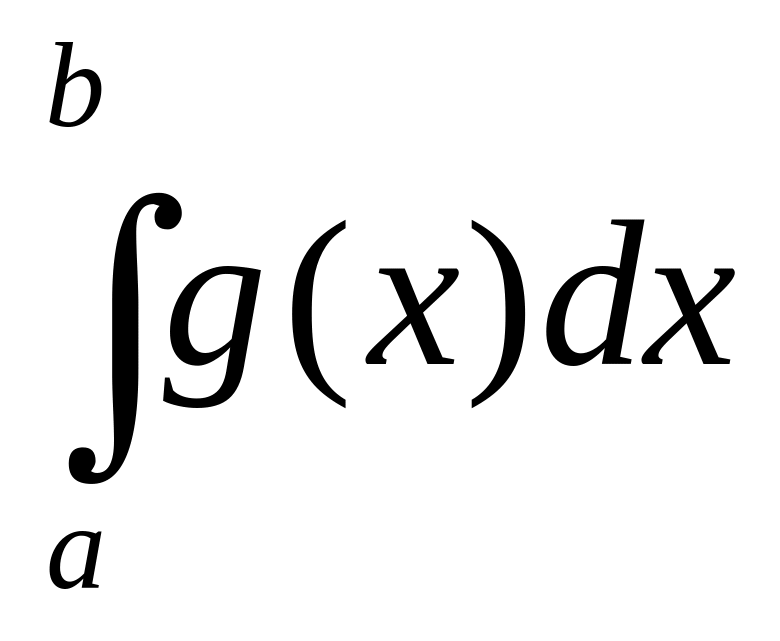 бөлейік, сонда
бөлейік, сонда
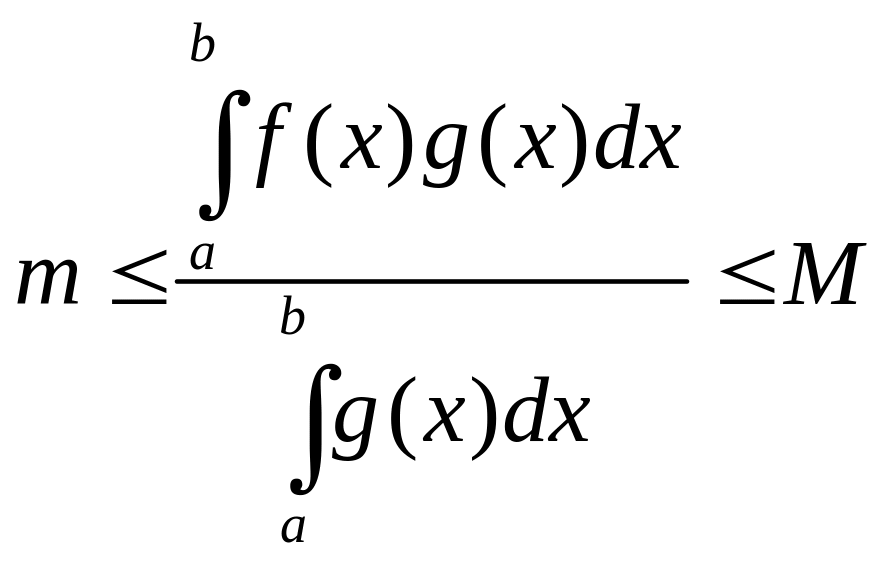
![]()
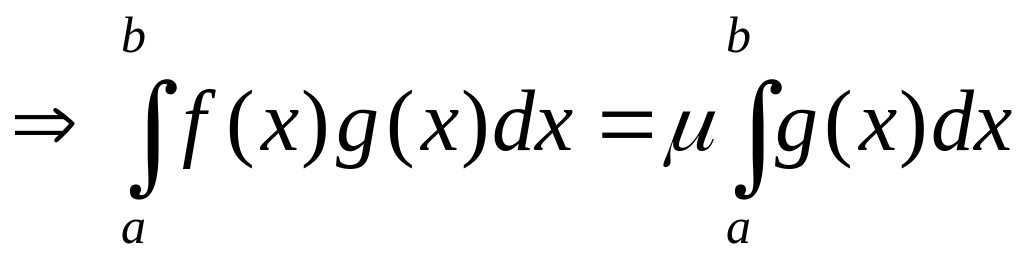
Дәлелденді.
Салдар:
Егер
![]() болса, онда
болса, онда
 ал бұдан
ал бұдан
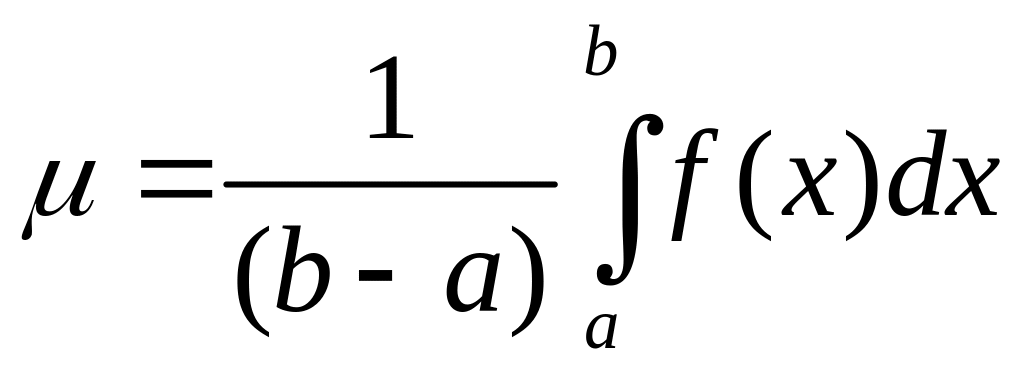
Орта мән туралы теорема 2
![]()
![]()
g(x),![]() монотонды
Бонне формуласы
монотонды
Бонне формуласы
дәлелдеу:
g(x)
монотонды, анықтық үшін монотонды өспелі
деп алайық, онда
![]()
![]()
![]()
![]()
![]()
