3.4.²ЭубхЩ³ызэ есбу»лЭ»сЗ п³йбхубхЩб

¸Зп³сПнбХ бг ·Н³ЫЗЭ С³Щ³П³с·бхЩ ³ЭубхЩ³ЫЗЭ есбу»лЭ»сЗ Пбс»сЗ П³йбхубхЩБ н»сЙбхН³П³Э »Х³Э³Пбн µ³н³П³Э ¹Ен³сЗЭ ¨ Н³н³ЙбхЭ ³ЯЛ³п³Эщ ¿: Ье³п³П³С³сЩ³с ¿ ы·п³·бсН»Й С³Щ³П³с·г³ЫЗЭ Щб¹»Й³нбсЩ³Э »Х³Э³ПЭ»сЗу Щ»ПБ` “Matlab Simullink” Нс³·ЗсБ: ²Ыл Щ»Гб¹ЗП³Ыбн С³н³щн³Н ¿ ЭП.13-бхЩ µ»сн³Н Щб¹»ЙБ: ВбХ³сПбхЩБ (Step) Зс³П³Э³унбхЩ ¿ t=0 е³СЗЭ, µ»йЗ С³н»ЙбхЩБ (Step1) t=4 е³СЗЭ:

ä³ñ³å ÁÝóóùáí ÃáÕ³ñÏÙ³Ý åñáó»ëÇ Ïáñ»ñÁ µ»ñí³Í »Ý Ýϳñ X–áõÙ н³сПЫ³Э п»Х³Щ³лбхЩ, бсп»ХЗу бсбЯнбхЩ »Э бс³ПЗ убху³ЭЗЯЭ»сБ:

²й³н»Й³·бхЫЭ ³с³·бхГЫбхЭЭ ¿ ω_max=82,94: ²é³í»É³·áõÛÝ Ñáë³ÝùÁ` I_max=164: Рбл³Эщбн С»п³¹³сУ П³еБ ЩЗ³ЭбхЩ ¿ ·бсНЭ³П³ЭбхЩ t=0 е³СЗЭ ¨ ПпснбхЩ t=t₁ å³ÑÇÝ:

асбЯбхЩ »Эщ ·»сП³с·³нбсбхЩБ ¨ Блп СблЭщЗ ·»сµ»йЭЩ³Э`

σ = (ω_max – ω_ëÝ) / ω₀ = (81-71,4) / 82,94 = 0.11

кп³пЗП лЛ³ЙБ ³Эн³Э³П³Э µ»йЗ ¹»ещбхЩ`

∆ω_c / ω₀ = (ω₀ – ω_ëÝ) / ω₀ = (82,94-71,4) / 82,94 =0.13

ÜÏ. 13

ÜÏ. 14

3.5.ºЭг³сПнбХ п³й³н³сЩ³Щµ ¿й»Ппс³µ³э»уЩ³э с³щ³п³с·

кп³пЗП лЛ³ЙЗ н»с³уЩ³Э ¨ ¹ЗЭ³ЩЗП убху³ЭЗЯЭ»сЗ Йн³уЩ³Э С³Щ³с Й³ЫЭ п³с³НбхЩ ¿ лп³у»Й §Щб¹»Й³ЫЗЭ ыепЗЩбхЩ¦ »Х³Э³ПБ:

о»ЩеЗ ³й³з³¹сЗг ¨ П³с·³нбсЗгЭ»с:

ЬП.15-бхЩ µ»сн³Н ¿ Л³сЗлЛЗ Сбл³ЭщЗ ¨ ³с³·бхГЫ³Э »ЭГ³сПнбХ П³й³н³сЩ³Щµ ¿Й»Ппс³µ³Э»уЩ³Э С³Щ³П³с·З лпсбхПпбхс³ЫЗЭ лЛ»Щ³Э:

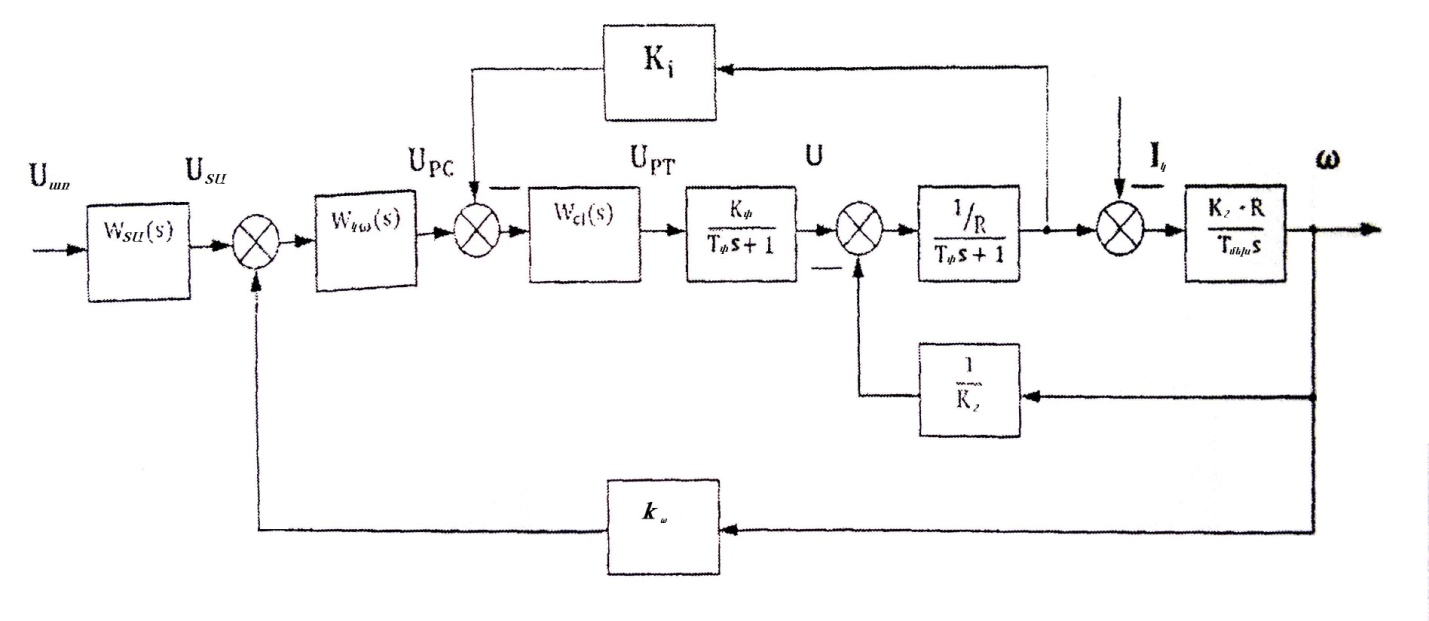
ÜÏ. 15

о»ЩеЗ о² ³й³з³¹сЗгБ С³·»убхЩбн ЗЭп»·сбХ ыХ³П ¿` ЭП.16

ÜÏ.16î»ÙåÇ ³é³ç³¹ñÇãÇ µÝáõó·ÇñÁ

²Ûëï»Õ -Б ГбХ³сПЩ³Э ³й³з³¹сн³Н Е³Щ³Э³ПЭ ¿: ²Ыл ¹»ещбхЩ ³й³з³¹сЗгЗ чбЛ³ЭуЩ³Э эбхЭПуЗ³Э ПЙЗЭЗ`

ÂáÕ³ñÏÙ³Ý ³í³ñïÇó Ñ»ïá ¨ С»п³·³ЫбхЩ µ»йЗ С³н»ЙЩ³Э Е³Щ³Э³П есбу»лЭ»сЭ БЭГ³ЭбхЩ »Э ³й³Эу о² Щ³лЭ³ПубхГБ³Э: Рбл³ЭщЗ C_I ¨ ³ñ³·áõÃÛ³Ý C_ω П³с·³нбсЗгЭ»сБ лбнбс³µ³с П³йбхунбхЩ »Э ые»с³уЗбЭ ъаф бхЕ»Х³с³сЭ»сЗ µ³½³ЫЗ нс³: афЕХ³с³сБ бхЭЗ л»ч³П³Э С»п³¹³сУ П³е, бсБ П³½Щн³Н ¿ R_ÑÏ, C_ÑÏ Ï³Ù K_ÑÏ (ПбЭп³ПпЗ ч³П) п³сс»сЗу (ЭП. 17): О³с·³нбсЗгЭ»сЗ µбЙбс U_Ùù, U_»Éù ³½¹³Ýß³ÝÝ»ñÁ ë³Ñٳݳ÷³Ïí³Í »Ý áõŻճñ³ñÝ»ñÇ ëÝÙ³Ý É³ñÙ³Ý ³é³í»É³·áõÛÝ U_úàõmax ³ñÅ»ùáí:

Îëï³Ý³Ýù ѻﳹ³ñÓ Ï³åÇ ·áñͳÏÇóÝ»ñÇ ³ñÅ»ùÝ»ñ`

ÁݹáõÝ»Ýù

²Ûëï»Õ U_imax ¨ U_ωmax–Б С»п³¹³сУ П³е»сЗ П³ебхХЗЭ»сЗ »ЙщЗ ³½¹­³Э­Я­³­Э­Э»с­­­­Э »Э:

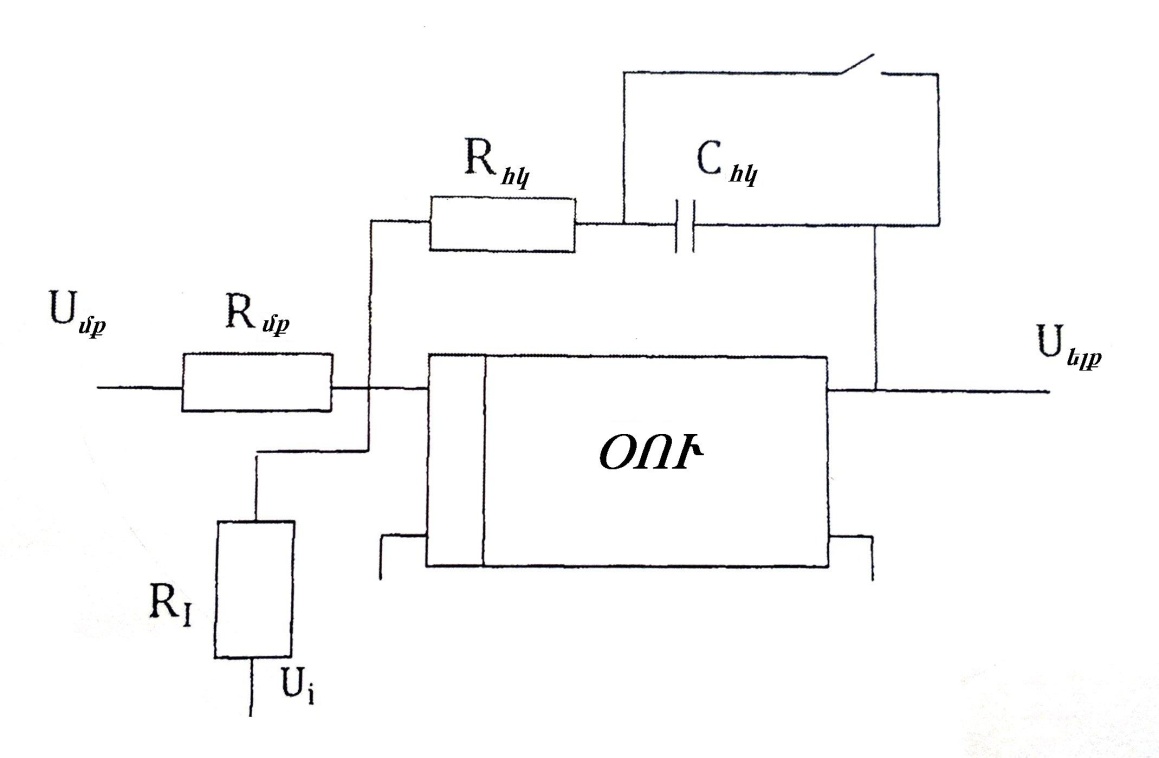
ÜÏ. 17

Р³Щ³У³ЫЭ §Щб¹»Й³ЫЗЭ ыепЗЩбхЩ¦ »Х³Э³ПЗ Сбл³ЭщЗ П³с·³нбсЗгЗ чб­Л³Э­­у­Щ³Э эбхЭПуЗ³Э ¿`

-PI пЗеЗ П³с·³нбсЗг:

ъепЗЩ³Й³ун³Н Сбл³ЭщЗ ПбЭпбхсЗ чбЛ³ЭуЩ³Э эбхЭПуЗ³Э ¿`

²с³·бхГЫ³Э П³с·³нбсЗг чбЛ³ЭуЩ³Э эбхЭПуЗ³Э ¿`

ЗлП ыепЗЩ³ун³Н ³с³·бхГЫ³Э ПбЭпбхсЗ чбчбЛЩ³Э эбхЭПуЗ³Э`

²ЫлеЗлЗ С³Щ³П³с·бхЩ N₂(s) ¨ N₃(s) µЭбхГ³·сбХ С³н³л³сбхЩЭ»сБ ыепЗЩ³Й³ун³Н »Э, щ³ЭЗ бс г»Э БЭ¹·сПбхЩ T_¿Ù, T_Ù»Ë Щ»Н Е³Щ³Э³ПЗ С³лп³пбхЭЭ»с:

д³с³е БЭГ³ущбн ГбХ³сПЩ³Э ¹»ещбхЩ ³с³·бхГЫ³Э ПбсБ бсбЯнбхЩ ¿`

µ³Ý³Ó¨Çó, ÇëÏ Ñáë³ÝùÇ ÏáñÁ`

µ³Ý³Ó¨Çó:

²Ûë Ïáñ»ñÇ ¹ÇݳÙÇÏ ¨ ëï³ïÇÏ óáõó³ÝÇßÝ»ñÁ ѳÛïÝÇ »Ý δ = 0, σ< 0.05:

´»йЗ С³н»ЙЩ³Э ¹»ещбхЩ ³с³·бхГЫ³Э ³ЭПЩ³Э ¹ЗЭ³ЩЗП³Э ЭП³с³·сн³Н ¿`

²ПЭС³Ып ¿, бс µ»йЗ С³н»ЙЩ³Э ¹»ещбхЩ ³с³·бхГЫ³Э лп³пЗП ³ЭПбхЩБ

кп³пЗП ³ЭПбхЩБ н»с³уЭ»Йбх С³Щ³с ПЗс³йнбхЩ ¿ PI пЗеЗ ³с³·бхГЫ³Э П³с·³нбсЗг`

гٳݳϳñ·Á ëï³ïÇÏ ¿ áã ÙdzÛÝ Áëï ϳé³í³ñÙ³Ý U_առ ³é³ç³¹ñ³ÝùÇ, ³Ûɨ I_աнс¹бнЩбхЭщЗ, щ³ЭЗ бс

¨ s = = 0

ВбХ³сПЩ³Э Е³Щ³Э³П ³с³·бхГЫ³Э ³ЭубхЩ³ЫЗЭ есбу»лБ ыепЗЩ³ун³Н ¿: о²-З ³йП³ЫбхГЫ³Э ¹»ещбхЩ ГбХ³сПЩ³Э Е³Щ³Э³ПЗ ¹ЗЭ³ЩЗП Сбл³ЭщБ л³СЩ³Э³ч³ПнбхЩ¿ t_³ – З БЭпсбхГЫ³Щµ, щ³ЭЗ бс`

ЬП. 18 ºЭГ³сПнбХ П³й³н³сЩ³Э »Й»Ппс³µ³Э»уЩ³Э »сППбЭпбхс С³Щ³П³с·З лП½µбхЭщ³ЫЗЭ ¿Й»Ппс³П³Э лЛ»Щ³Э

²é³Ýó ѻﳹ³ñÓ Ï³å»ñÇ

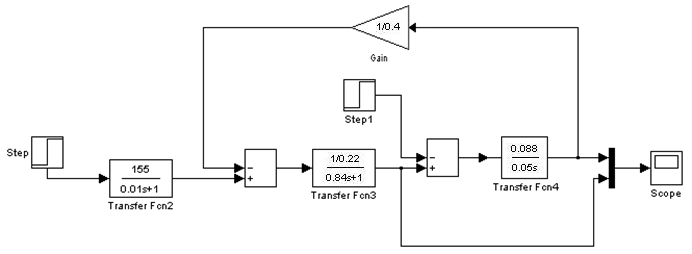
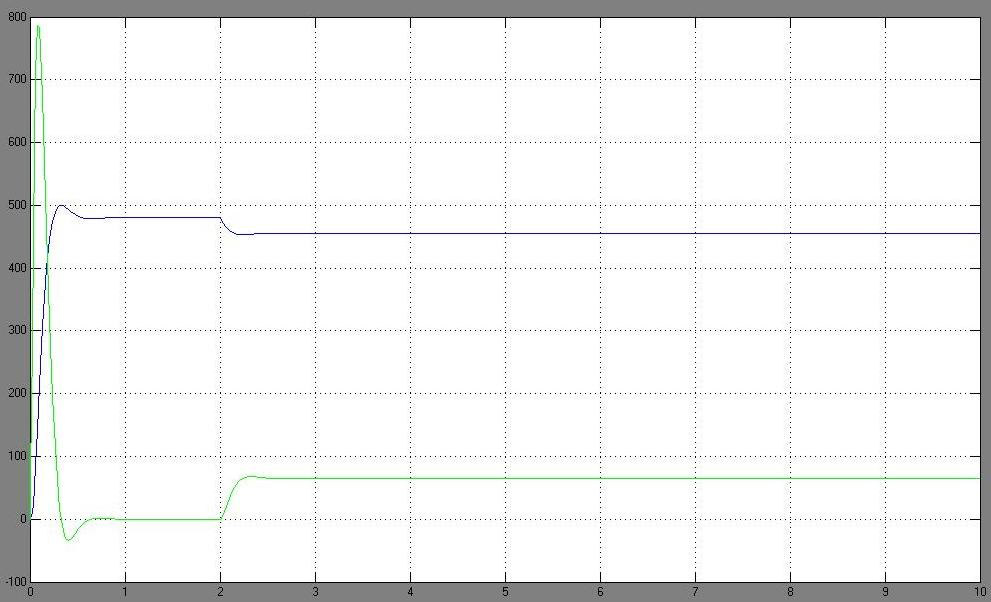
ÜÏ. 19