13 Расчёт прочности элементов с тавровым и двутавровым профилем

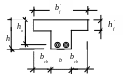
Тавровое сечение состоит из полки и ребра. Обычно в практике встречается тавровое сечение с полкой в сжатой зоне. В сравнении с прямоугольным сечением тавровое сечение экономичнее, так как при одной и той же несущей способности элемента в нём расходуется меньше бетона вследствие сокращения размеров растянутой зоны. Сжимающие напряжения в полках тавровых балок уменьшаются от ребра к краям полки, поэтому пункт 3.16 СНиП 2.03.01-84^* ограничивает ширину свеса полки, вводимой в расчёт. Ширина b_f^' вводится в расчёт из условия, что ширина свесов полки в каждую сторону от ребра должна быть не более 1/6 пролёта элемента и не более при наличии поперечных рёбер или при h_f^'0.1h - 1/2 расстояния в свету между продольными рёбрами. При решении задач сечений, имеющих полку с нейтральной линией проходящей в ней, рассматривается, в первую очередь значение момента, которое может воспринимать полка. Если внешний момент сжатия больше момента воспринимаемого полкой M>M_f , x<h_f^' , то нейтральная линия будет проходить в ребре, а если момент меньше или равен моменту воспринимаемому полкой M<M_f , x<h_f^' , то нейтральная линия проходит в полке. При решении задач рассматривается, как правило, работа тавровых сечений конструкции с нейтральной линией проходящей в полке. Этот случай расчёта считается случаем №1.

Если нейтральная линия проходит в полке, дополняем сечение до прямоугольного с координатами b_f^' и h_o и решаем задачи аналогично алгоритму задач 1-го типа изгибаемых элементов с одинарным или двойным армированием. M_f^'=b_f^' h_f^'R_b(h_o-0.5 h_f^'). Если при расчёта условие _m>_R , то в сжатой зоне бетона необходимо установить сжатую зону арматуру и применить двойное армирование. Решение задачи сводится к определению h_o, b, h,Q, M_u, и определения A_s и A_s^'.

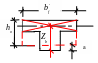
Если нейтральная линия проходит в ребре - это случай №2. Алгоритм решения задач тавровых сечений, если нейтральная линия проходит в ребре:

1. M>M_f;

2. Определяем момент воспринимаемый свесом: M_OV=R_b( b_f^'-b) h_f^'(h_o-0.5 h_f^');

3. Определяем площадь арматуры, приходящейся на свесы:

4. Определяем момент, приходящийся на ребро: M_b1=M- M_OV;

5. Определяем значение:

6) Если _m<_R определяем площадь арматуры, приходящейся на ребро:

Если условие не выполняется, то на один модуль увеличиваем высоту или ширину сечения на одну ступень, увеличиваем класс бетона или устанавливаем арматуру в сжатой зоне. 7) A_s=A_s1+As_OV

Для того чтобы проверить несущую способность таврового сечения по случаю №2:

1) находим общую площадь арматуры, приходящейся на свесы:

2) Определяем площадь арматуры, приходящейся на ребро: _As1=A_s+As_OV.

3) Определяем коэффициент армирования ребра: =А_s1/(bh_o);

4)

5) Определяем расчётный изгибающий момент, воспринимаемый ребром: M_b1=_mR_bbh_o²;

6) Определяем момент свеса: M_OV=R_b( b_f^'-b) h_f^'(h_o-0.5 h_f^');

7) Определяем момент, воспринимаемый тавровым сечениям: M_u=M_b1+M_OV, M_uM.