Методи розрахунку статично невизначних систем
Статично невизначеної називається така система, що не може бути розрахована за допомогою одних тільки рівнянь статики, тому що має зайві зв'язки. Для розрахунку таких систем складаються додаткові рівняння, що враховують деформації системи.
Обмовимося, що тут і далі поняття “розрахунок” має на увазі тільки побудова епюр внутрішніх силових факторів, що виникають в елементах системи, а не розрахунок на міцність, твердість і т.д.
Статично невизначені системи володіють поруч характерних рис:
1. Статично невизначені конструкції є більш твердими, чим відповідні статично визначні, тому що мають додаткові зв'язки.
2. У статично невизначених системах виникають менші внутрішні зусилля, що визначає їхня економічність у порівнянні зі статично визначними системами при однакових зовнішніх навантаженнях.
3. Порушення зайвих зв'язків у статично невизначеній системі не завжди приводить до руйнування, у той час як утрата зв'язку в статично визначній системі робить неї геометрично змінюваної.
4. Для розрахунку статично невизначених систем необхідно попередньо задаватися геометричними характеристиками поперечних переріз елементів, тобто фактично їхньою формою і розмірами, тому що їхня зміна приводить до зміни зусиль у зв'язках і новому розподілі зусиль у всіх елементах системи.
5. При розрахунку статично невизначених систем необхідно заздалегідь вибрати матеріал конструкції, тому що необхідно знати його модулі пружності.
6. У статично невизначених системах температурний вплив, осідання опор, неточності виготовлення і монтажу викликають появу додаткових зусиль.
Основними методами розрахунку статично невизначених систем є:
1.Метод сил. Тут у якості невідомих розглядаються зусилля – сили і моменти.
2.Метод переміщень. Невідомими є деформаційні фактори – кути поворотів і лінійні зсуви.
3.Змішаний метод. Тут частина невідомих являє собою зусилля, а інша частина – переміщення.
4.Комбінований метод. Використовується при розрахунку симетричних систем на несиметричні навантаження. Виявляється, що на симетричну складову заданої навантаження систему доцільно розраховувати методом переміщень, а на назад симетричну складову – методом сил.
Крім зазначених аналітичних методів при розрахунку особливо складних систем використовуються різні чисельні методи.
Метод сил. Ідея методу. Основні невідомі. Основна система методу сил. Канонічні рівняння та їх зміст. Наведіть приклад.
Одним із перших методів розрахунку статично невизначених систем є метод сил. За основні (зайві) невідомі в методі сил (method of forces) беруть узагальнені реактивні сили в відкинутих зв’язках системи. Число зайвих невідомих зв’язків називають ступенем статичної невизначеності. Для обчислення ступеня статичної невизначеності рам можна використовувати простішу формулу, ніж формула Чебишова [3]:
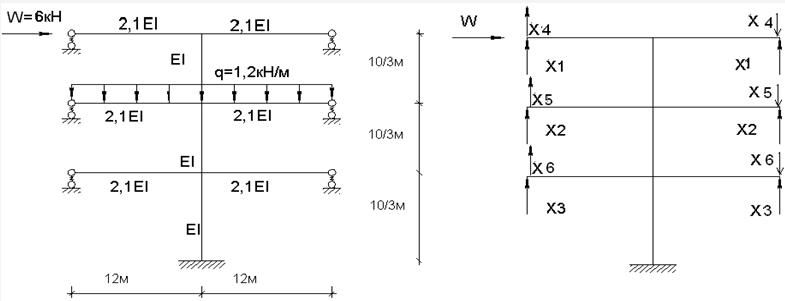
де Л – число зайвих зв’язків. К – кількість ізольованих контурів рами, для плоских стержневих систем – це кількість площин, обмежених стержнями рами або стержнями рами і “землею” (“землю” слід вважати одним простим диском) [3]. Ш – загальна кількість простих шарнірів (разом з опорними та шарнірами кінематичних в’язей. Одиночний простий шарнір з’єднує два диски). Шарнірно нерухому опору слід розглядати як простий шарнір, а шарнірно рухому – як два простих шарніри [3]. Розрахунок внутрішніх зусиль за методом сил в статично невизначеній рамі, зображеній на рис. 2.1.1, проводиться в такій послідовності: а) ступінь статичної невизначеності (degree of static indefinability) рами:
б)
для вибору основної системи методу
сил відкинемо 6 зайвих зв’язків
та розкладемо невідомі реакції в них
на симетричні та кососиметричні пари,
рис. 2.1.2. Це дасть можливість взяти до
розгляду шість пар невідомих X1, X2,
X3 , X4, X5, в) запишемо канонічні рівняння методу сил, які вказують на те, що переміщення за напрямком відкинутих зв’язків мають бути нульовими, оскільки в заданій рамі в цих точках знаходяться опори, які не допускають переміщень по вертикалі. В результаті отримуємо систему лінійних алгебраїчних рівнянь (equation) шостого порядку (2.1.3).
де
г)
для визначення коефіцієнтів
канонічних рівнянь (quotients of the
initial equations) методу
силбудуються епюри згинальних моментів
в основній системі від парних одиничних
зайвих невідомих Хi =1, i=1 д) розв’язавши систему канонічних рівнянь методу сил одержимо корені системи:
е) кінцеві епюри згинальних моментів та поперечних сил будуємо за формулами:
де Мпр, Мл – кінцеві значення згинальних моментів в окремо взятому стержні справа і зліва;
ж) для побудови епюри поздовжніх сил доцільно розглядати рівняння рівноваги для кожного вузла (рис. 2.1.6) в кінцевій епюрі.
Рисунок 2.1.1 – Розрахункова схема Рисунок 2.1.2 – Основна система методу сил
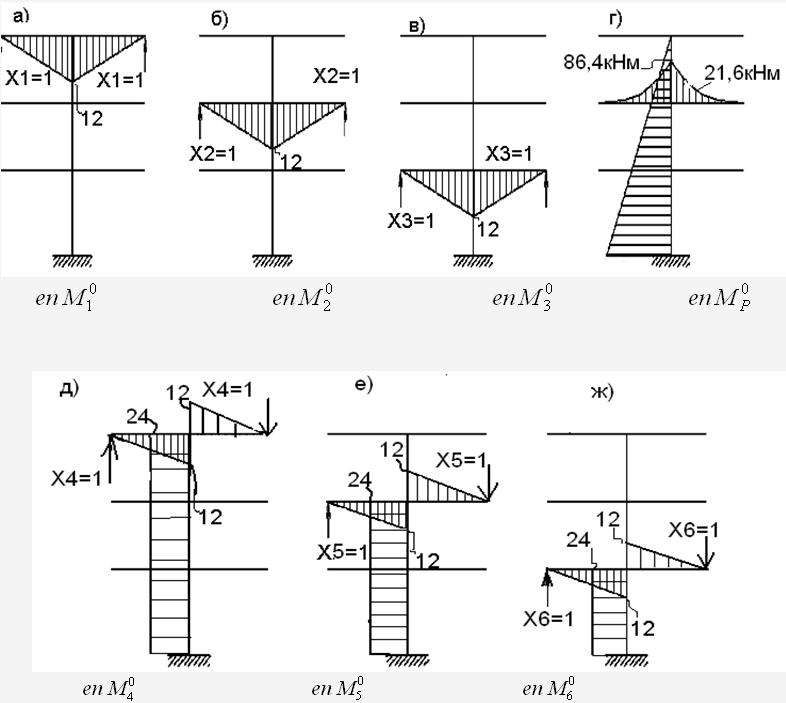
Рисунок
2.1.3 – Епюри згинальних моментів
в основній системі методу сил від: а,
б, в, д, е, ж – лінійних одиничних
невідомих
Рисунок
2.1.4 – Кінцева епюра згинальних
моментів
Кінематична
перевірка епюри моментів:
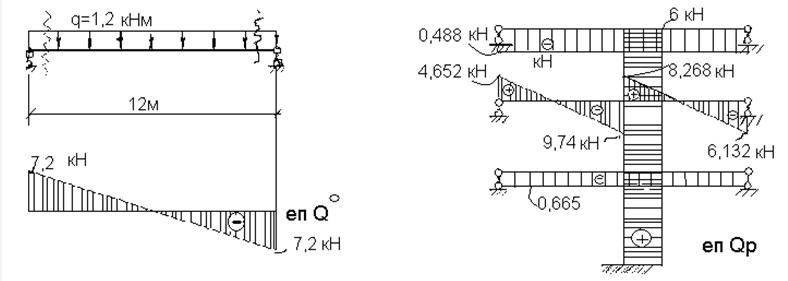
Рисунок 2.1.5 – Етапи отримання епюри поперечних сил Qр
Рисунок 2.1.6 – Етапи побудови епюри поздовжніх сил Np |
|||||||||||||||
|
=
-Л.
–
одиничні переміщення в основній
системі методу сил в напрямку “і”
від дії одиничної сили Xj =
1;
–
вантажні
переміщення в напрямку “і” від дії
зовнішнього навантаження P, визначаються
інтегруванням відповідних епюр за
залежностями Максвела-Мора або за
формулами числового інтегрування
(за формулами Верещагіна,
Мюллера-Бреслау чи Сімпсона-Карнаухова);
6
та від зовнішнього
навантаження (external loading),
рис. 2.1.3;
,
,
–
епюра поперечних сил в окремому
стержні від зовнішнього навантаження
побудована в припущенні, що цей
стержень шарнірно
обпертий (articulated about); 
, 
, 
, 
, 
, 
та
г) – від зовнішнього навантаження
,
статична перевірка вузлів та сумарна
одинична епюра 
