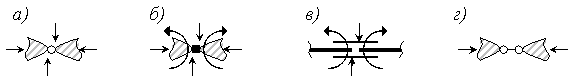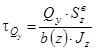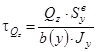- •Кінематичний аналіз розрахункових схем, його необхідність та складові частини. Наведіть приклад.
- •Дайте визначення понять внутрішніх зусиль в перерізах плоских стержневих систем та правило їх знаків.
- •Для вирішення яких задач Будівельної механіки використовують внутрішні зусилля
- •Методи розрахунку статично невизначних систем
- •Метод сил. Ідея методу. Основні невідомі. Основна система методу сил. Канонічні рівняння та їх зміст. Наведіть приклад.
- •Метод переміщень. Ідея методу. Основні невідомі. Основна система методу переміщень. Канонічні рівняння та їх зміст. Наведіть приклад.
- •7.4 Алгоритм расчета систем методом перемещений
- •Метод переміщень. Розгорнута форма методу переміщень. Основні невідомі. Рівняння рівноваги та їх зміст. Наведіть приклад.
- •7.4 Алгоритм расчета систем методом перемещений
- •Змішаний метод. Ідея методу. Основні невідомі. Основна система змішаного методу. Канонічні рівняння та їх зміст. Наведіть приклад.
- •Основные теоретические положения
- •3. Пример выполнения индивидуального расчетного задания
- •3.1. Исходные данные
- •3.2. Выбор рационального метода расчета заданной рамы
- •3.3. Построение необходимых эпюр внутренних усилий в единичных и грузовом состояниях ос см
- •3.4. Вычисление коэффициентов при неизвестных и свободных членов ску см
- •3.5. Построение эпюр внутренних усилий
- •3.6. Статическая и кинематическая проверка результатов расчетов
Кінематичний аналіз розрахункових схем, його необхідність та складові частини. Наведіть приклад.
При знаходженні напружено-деформованого стану (НДС) споруди її заміняють спрощеним поданням - розрахунковою схемою, вільною від другорядних невизначальних факторів, просторовою чи плоскою. Якщо осі всіх елементів споруди і навантаження розташовані в одній площині - це плоска розрахункова схема. Плоскі розрахункові схеми є найбільш простими і дозволяють в більшості випадків отримати задовільну для практики точність розрахунку. Споруди (в подальшому - розрахункові схеми) в змозі сприймати навантаження лише в випадку, коли вони зберігають надану при їх спорудженні структуру, тобто геометричну форму і положення. Системи, що змінюються, не в змозі урівноважити зовнішні сили і при їх дії приходять в рух, змінюючи свою форму. Такі системи в будівництві не використовуються як споруди. Споруда має бути нерухомою відносно основи, структурно чи геометрично незмінною, а зміна її форми має йти лише за рахунок деформацій елементів. В геометрично незмінних спорудах малим деформаціям елементів відповідають малі переміщення точок споруди. Таким чином кінематичний аналіз споруди (розрахункової схеми) має передувати розрахунку її напружено-деформованого стану. Змінність внутрішньої структури і рухомості споруди характеризується ступенем вільності – числом незалежних геометричних параметрів, що визначають положення всіх елементів споруди. Геометрична незмінність споруди визначається в такій послідовності.
Крім шарнірних з’єднань диски пов’язуються:
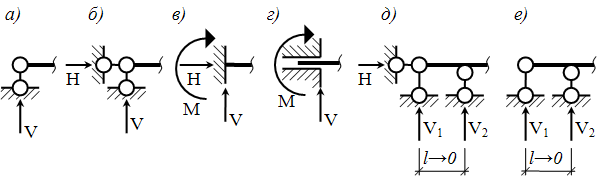
Рисунок 1.1.1 – Види опорних закріплень: а) - шарнірно рухома опора, б) - шарнірно нерухома опора, в) - жорстке нерухоме закріплення, г) - жорстке рухоме закріплення (проковзуюче закріплення), д, е) - шарнірно стержневі еквіваленти жорсткого та проковзуючого закріплень
Вищезгадані з’єднання можна взаємно замінювати, їх ще називають в’язями, а сили що в них виникають – реакціями (рис. 1.1.2). Так шарнірний зв’язок, що усуває 2 лінійні поступальні переміщення можна взаємо замінити двома кінематичними в’язями або навпаки. Кожний опорний стержень еквівалентний одному зв’язку, оскільки не допускає переміщення диска в напрямку стержня (рис.1.1.1 а-е). Таким чином, ступінь вільності W споруди - кількісна оцінка кінематичного аналізу споруди, що складається із Д дисків, з’єднаних Ш простими шарнірами та має С0 опорних стержнів, можна визначити з формули П. Л. Чебишова [3, 8, 14]:
Кількісну характеристику змінюваності системи – ступінь геометричної змінюваності Г можна визначити з модифікованої формули П. Л.Чебишова [3]:
де Д – кількість простих дисків, включаючи опорний диск “землю”, якщо система прикріплена до неї; В – кількість матеріальних точок, тобто вузлів, в яких з’єднуються лише кінематичні в’язі; П – кількість простих припайок; Ш – кількість простих шарнірів; С – кількість кінематичних в’язів, (стержнів); 3 – число ступенів свободи всієї плоскої розрахункової схеми [3].
Рисунок 1.1.2 – Кінематичні в’язі: а) - шарнірна в’язь, б) - припайка, в) - муфта, г) - кінематична в’язь Для ферм (стержневих систем, з’єднаних ідеальними шарнірами) ступінь вільності W:
де Y – число вузлів ферми, С – число внутрішніх стержнів ферми, С0 – число опорних стержнів. Умова геометричної незмінності:
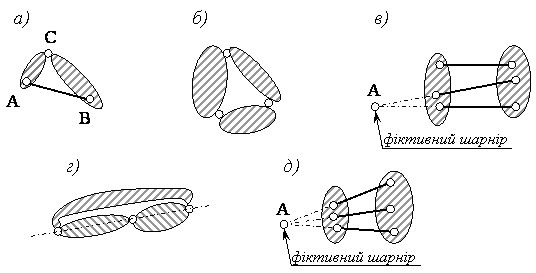
2. Виконання умови (1.1.3) необхідно, але недостатньо для забезпечення геометричної незмінності споруди, яка залежить не лише від числа зв’язків, накладених на диски, але й від їх розташування. Якщо умова (1.1.3) виконується, перевіряють ще геометричну структуру споруди (проводять якісну оцінку кінематичного аналізу). Для цього виділяють диски і досліджують їх з’єднання між собою, враховуючи основні принципи утворення структурно незмінних систем (рис. 1.1.3, а –в). Два диски можна з’єднати жорстко шарніром С і стержнем АВ, вісь якого не проходить через центр шарніра (рис. 1.1.3, а). Три диски можна з’єднати за допомогою трьох шарнірів, що не лежать на одній прямій (рис. 1.1.3, б). Два диски можна жорстко з’єднати трьома стержнями, що не перетинаються в одній точці і не паралельні один одному (рис. 1.1.3, в). Це аналогічно рис. 1.1.3, а, оскільки два стержня можна замінити фіктивним шарніром в точці А. Крім геометрично змінних та геометрично незмінних систем існують миттєво змінні системи. Такі системи одержимо, якщо три диски об’єднаємо трьома шарнірами, що лежать на одній прямій (рис. 1.1.3, г), або якщо два диски з’єднаємо трьома стержнями осі яких перетинаються в одній точці – миттєвому центрі обертання, (рис. 1.1.3, д). Миттєво змінні системи не є інженерними спорудами. Слід також пильнувати, щоб система не була близькою до миттєвої змінної. Тому кінематичний аналіз має включати аналіз і на миттєву змінність.
Рисунок 1.1.3 – Принципи утворення структурно-незмінних систем
Таким чином кінематичний аналіз включає етапи:
Статичною ознакою геометричної змінності є невизначеність зусиль або наявність нескінченно великих зусиль від кінцевого навантаження. Для визначення реакцій у в’язях (basicreactions) використовуються рівняння статики (static’sequations). |
||||||||||||
|
Приклад 1. Виконати кінематичний аналіз системи (рис.1.10,а).
Визначаємо ступінь свободи системи по формулі П.Л.Чебишева:
|
(1.3) |
де Д – число дисків, Ш – число простих шарнірів, С0 – кількість стержнів.
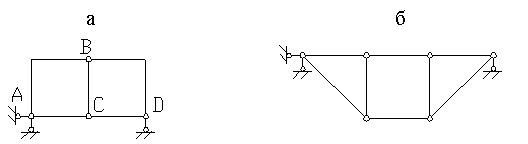
Рис.1.10
Відкидаючи
всі шарніри й опорні стержні, знаходимо,
що система складається з п'яти дисків
(![]() ).
Відкидаючи опорні стержні, визначаємо
число шарнірів, приведених до простих
(
).
Відкидаючи опорні стержні, визначаємо
число шарнірів, приведених до простих
(![]() :
по двох у точках
:
по двох у точках ![]() і
і ![]() ,
по одному – у точках
,
по одному – у точках ![]() і
і ![]() ).
Число опорних стержнів –
).
Число опорних стержнів – ![]() .
.
![]()
тобто
система може бути геометрично незмінною
й статично невизначеною. Щоб переконатися,
що це так, виконаємо аналіз структури
системи. Тому що диски ![]() ,
, ![]() і
і ![]() зв'язані
трьома шарнірами
,
і
,
що не лежать на одній прямій, то вони
утворять диск, до якого жорстко приєднаний
диск
зв'язані
трьома шарнірами
,
і
,
що не лежать на одній прямій, то вони
утворять диск, до якого жорстко приєднаний
диск ![]() за
допомогою шарніра
й
стержня
за
допомогою шарніра
й
стержня ![]() ,
вісь якого не проходить через центр
шарніра. Ця незмінна фігура жорстко
приєднана до землі за допомогою трьох
стержнів, що не перетинаються в одній
точці. Таким чином, система (рис.1.10,а)
геометрично незмінна й не є миттєво
змінюваною.
,
вісь якого не проходить через центр
шарніра. Ця незмінна фігура жорстко
приєднана до землі за допомогою трьох
стержнів, що не перетинаються в одній
точці. Таким чином, система (рис.1.10,а)
геометрично незмінна й не є миттєво
змінюваною.
Приклад 2. Виконати кінематичний аналіз системи (рис.1.10,б).
Тому що система є шарнірно-стержневою, то для визначення її ступеня свободи використовуємо формулу
|
(1.4) |
де ![]() –
число вузлів ферми;
–
число внутрішніх стержнів;
–
число вузлів ферми;
–
число внутрішніх стержнів; ![]() –
число опорних стержнів.
–
число опорних стержнів.
Тут ![]() ,
, ![]() ,
,
отже,
,
,
отже,
![]()
Таким чином, система має один ступінь свободи, є механізмом і не може використовуватися як будівельна конструкція.
Приклад 3. Дослідити систему (рис.1.11,а).
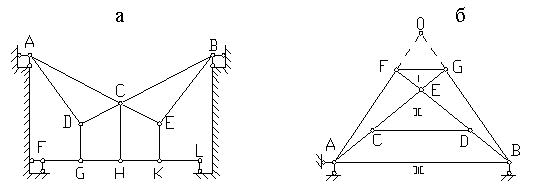
Рис.1.11
Ступінь свободи системи визначимо по формулі (1.3):
|
|
Отже,
система має два зайві зв'язки. Щоб
переконатися в її геометричній
незмінюваності, проаналізуємо структуру
системи. Тут можна виділити два незмінних
трикутники ![]() й
й![]() ,
які жорстко з'єднані один з одним і з
землею (розглянутою як диск) за допомогою
трьох шарнірів
,
які жорстко з'єднані один з одним і з
землею (розглянутою як диск) за допомогою
трьох шарнірів ![]() не
лежачих на одній прямій. Стержень
не
лежачих на одній прямій. Стержень ![]() прикріплений
до цієї незмінної частини системи за
допомогою шарніра
прикріплений
до цієї незмінної частини системи за
допомогою шарніра ![]() й
стержня
й
стержня ![]() ,
що не проходить через центр шарніра,
так само як і стержень
,
що не проходить через центр шарніра,
так само як і стержень ![]() за
допомогою шарніра
за
допомогою шарніра ![]() й
опорного стержня
й
опорного стержня ![]() .
Стержні
.
Стержні ![]() й
й ![]() –
зайві, тому що й без них система незмінна.
–
зайві, тому що й без них система незмінна.
Приклад 4. Виконати кінематичний аналіз системи (рис.1.11,б).
Використовуючи формулу (1.4), визначаємо число ступенів свободи системи:
![]()
отже, система має необхідну кількість зв'язків, щоб бути геометрично незмінною й статично визначеною.
Проаналізуємо
структуру. Виділимо незмінні
трикутники ![]() й
й ![]() .
Стержень
становить
єдине ціле із землею (третій диск), тому
що прикріплюється трьома опорними
стержнями, що не перетинаються в одній
точці. Щоб перевірити, чи жорстко з'єднані
диски І, ІІ, ІІІ (рис.1.11,б), переконаємося,
що три їхніх миттєвих центри обертання
не лежать на одній прямій. Шарнір
.
Стержень
становить
єдине ціле із землею (третій диск), тому
що прикріплюється трьома опорними
стержнями, що не перетинаються в одній
точці. Щоб перевірити, чи жорстко з'єднані
диски І, ІІ, ІІІ (рис.1.11,б), переконаємося,
що три їхніх миттєвих центри обертання
не лежать на одній прямій. Шарнір ![]() є
миттєвим центром обертання дисків І й
ІІ, а також дисків ІІ й ІІІ, тому що тут
перебуває фіктивний шарнір, що заміняє
стержні
й
,
що з'єднують ці два диски. Отже, система
миттєво змінювана, тому що де б не
перебував миттєвий центр обертання О
дисків І й ІІІ, через нього й точку
завжди
можна провести пряму, на якій будуть
лежати всі три миттєвих центри обертання.
є
миттєвим центром обертання дисків І й
ІІ, а також дисків ІІ й ІІІ, тому що тут
перебуває фіктивний шарнір, що заміняє
стержні
й
,
що з'єднують ці два диски. Отже, система
миттєво змінювана, тому що де б не
перебував миттєвий центр обертання О
дисків І й ІІІ, через нього й точку
завжди
можна провести пряму, на якій будуть
лежати всі три миттєвих центри обертання.
Алгоритм визначення внутрішніх зусиль в статично визначних системах. Наведіть приклад. Чи виникають внутрішні зусилля в перерізах статично визначних систем при температурних впливах та нерівномірному осіданні опор?
Внешние силы, действующие на конструкцию, разделяют на активные силы (нагрузку) и реакции опор. По характеру действия различают сосредоточенные силы, измеряемые в ньютонах (Н, кН), распределенную нагрузку, измеряемую в ньютонах на метры (Н/м, кН/м), если нагрузка распределена вдоль линии, или в ньютонах на метр квадратный (Н/м2, кН/м2), если нагрузка распределена по поверхности, сосредоточенный момент, измеряемый в ньютонометрах (Нм, кНм) (рис. 1.2). Реакции опор вычисляют через активные силы методами теоретической механики.
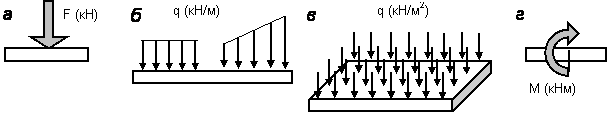
Рис. 1.2. Виды внешних нагрузок: а – сосредоточенная сила; б – распределенная по длине стержня нагрузка; в – распределенная по поверхности пластинки нагрузка; г – сосредоточенный момент
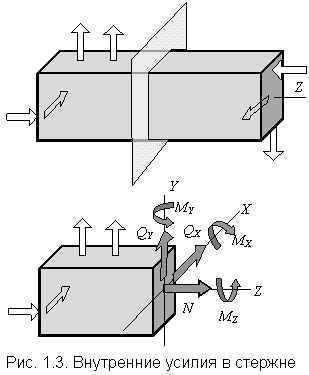
|
Под действием внешних сил стержень деформируется, при этом между отдельными частями стержня появляются дополнительные силы взаимодействия, называемые внутренними силами. Если стержень мысленно рассечь плоскостью, перпендикулярной к продольной оси стержня Z, то по всей площади поперечного сечения от одной части стержня на другую часть будут передаваться внутренние силы.Отбросим правую часть стержня. Внутренние силы, передающиеся от неё на левую часть (рис. 1.3), по отношению к левой части стержня становятся внешними силами и могут быть представлены главным вектором и главным моментом. Центром приведения принимается центр тяжести поперечного сечения стержня, через который проводят координатные оси X,Y, лежащие в плоскости сечения, и ось Z, перпендикулярную плоскости поперечного сечения. Главный вектор раскладывается на силы N, Qx, Qy, а главный момент – на моменты Mx, My, Mz. Указанные шесть величин называют внутренними усилиями (внутренними силовыми факторами) стержня. Каждое из них имеет своё название: N – продольная (нормальная) сила,Qx и Qy – поперечные (перерезывающие) силы, Мх и Мy – изгибающие моменты, Мz – крутящий момент. Для определения внутренних усилий используют метод сечений. Он заключается в выполнении четырех действий: разрезать стержень плоскостью поперечного сечения на две части; отбросить одну из частей стержня; заменить действие отброшенной части стержня на оставшуюся часть внутренними усилиями; уравновесить оставшуюся часть стержня. В общем случае можно составить шесть уравнений равновесия: суммы проекций всех сил на оси X, Y, Z и суммы моментов всех сил относительно этих осей. |
Для расчёта всех статически определимых систем достаточно решать уравнения равновесия:
Для плоских задач есть три условия равновесия. Сумма всех вертикальных сил, всех горизонтальных сил и всех моментов должна быть равна нулю. Σ V=0, Σ H=0, Σ M=0.
Для пространственных задач есть шесть условий. Σ X=0, Σ Y=0, Σ Z=0, Σ Mx=0, Σ My=0, Σ Mz=0.
Осадка опор, температурные воздействия (лише при рівномірному нагріванні і однорідній конструкції) и неточности сборки в статически определимых системах не влияют на распределение и величину усилий, що зумовлено їх статичною визначністю(довжина цих елементів вільно змінюється)
Рівняння статики |
Визначається |
Напруження |
|
Поздовжня
сила |
|
|
Поперечна
сила |
|
|
Поперечна
сила |
|
|
Крутний
момент |
|
|
Згинальний
момент |
|
|
Згинальний
момент |
|
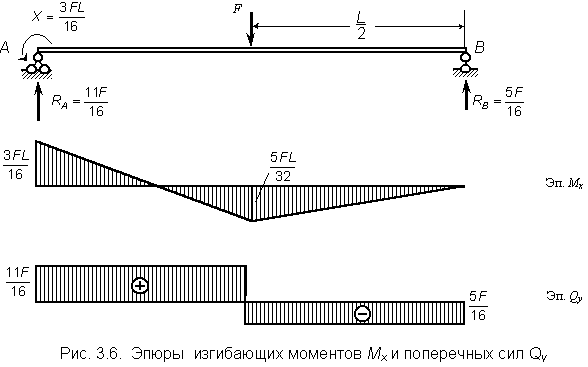
Построение эпюр Mx, Qy для заданной балки показано на рис. 3.6 и дополнительных пояснений не требует.