2. Технология решения задач линейного программирования с помощью microsoft excel

2.1. Условие задачи

Для изготовления трех видов изделий А, В и С используется токарное, фрезерное, сварочное и шлифовальное оборудование. Затраты времени на обработку одного изделия для каждого из типов оборудования указаны в табл. 2.1. Там же указан общий фонд рабочего времени каждого из типов используемого оборудования, а также прибыль от реализации одного изделия данного вида.

Таблица 2.1

Исходные данные

Оборудование	А	В	С	ОФРВ (ч)
Фрезерное	2	4	5	120
Сварочное	1	8	6	580
Токарное	7	4	5	340
Шлифовальное	4	6	7	360
Прибыль/ед. (руб.)	10	14	12

Требуется определить, сколько изделий каждого вида следует изготовить предприятию, чтобы прибыль от их реализации была максимальной.

2.2. Математическая модель задачи

Предположим, что будет изготовлено  единиц изделий вида А,  единиц – вида В и  единиц – вида С. Тогда для производства такого количества изделий потребуется затратить  станко-часов фрезерного оборудования. Так как общий фонд рабочего времени станков данного типа не может превышать 120, то должно выполняться неравенство

.

Аналогичные рассуждения относительно возможного использования сварочного, токарного и шлифовального оборудования приведут к следующим неравенствам:

При этом, так как количество изготовляемых изделий не может быть отрицательным, то

. (2.1)

Далее, если будет изготовлено  единиц изделий вида А,  единиц изделий вида В и  единиц изделий вида С, то прибыль от их реализации составит

.

Таким образом, приходим к следующей математической задаче: дана система

(2.2)

четырех линейных неравенств с тремя неизвестными  и линейная функция относительно этих же переменных

. (2.3)

Требуется среди всех неотрицательных решений системы неравенств (2.2) найти такое, при котором функция (2.3) принимает максимальное значение.

Линейная функция (2.3), максимум которой требуется определить, вместе с системой неравенств (2.2) и условием неотрицательности переменных (2.1) образуют математическую модель исходной задачи.

Так как функция (2.3) линейная, а система (2.2) содержит только линейные неравенства, то задача является задачей линейного программирования.

2.3. Решение задачи с помощью Microsoft Excel

1. Подготовим форму для ввода условий (Рис. 2.3.1).

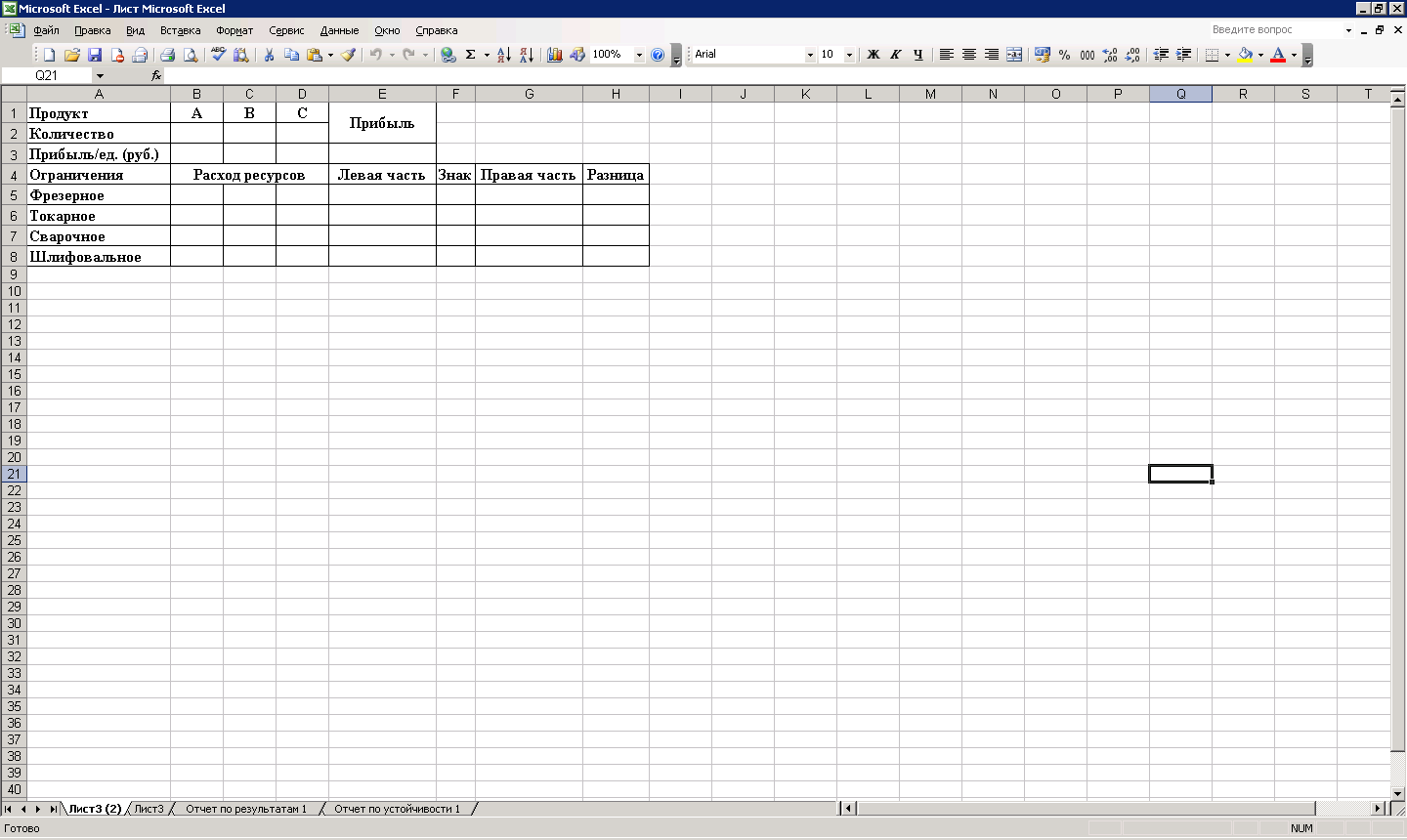
Рис. 2.3.1. Форма для ввода данных

2. В задаче оптимальные значения вектора X=(Х₁, Х₂, Х₃) будут помещены в ячейках В2:D2, оптимальное значение целевой функции – в ячейке E3.

3. Введём исходные данные в созданную форму. Получим результат, показанный на рис. 2.3.2.

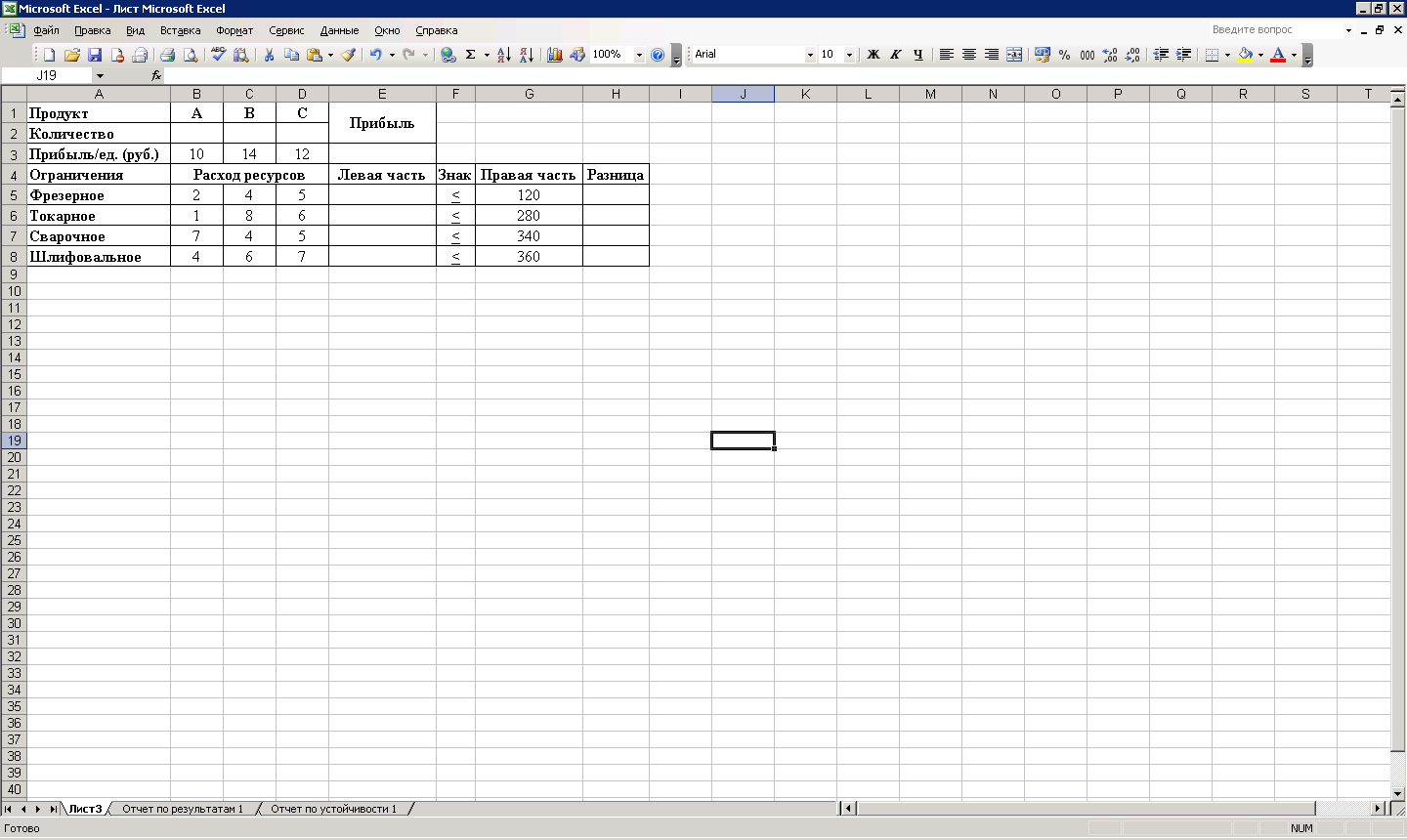
Рис. 2.3.2. Форма с исходными данными

4. Введём зависимость для целевой функции и для левых частей ограничений (Рис 2.3.3).

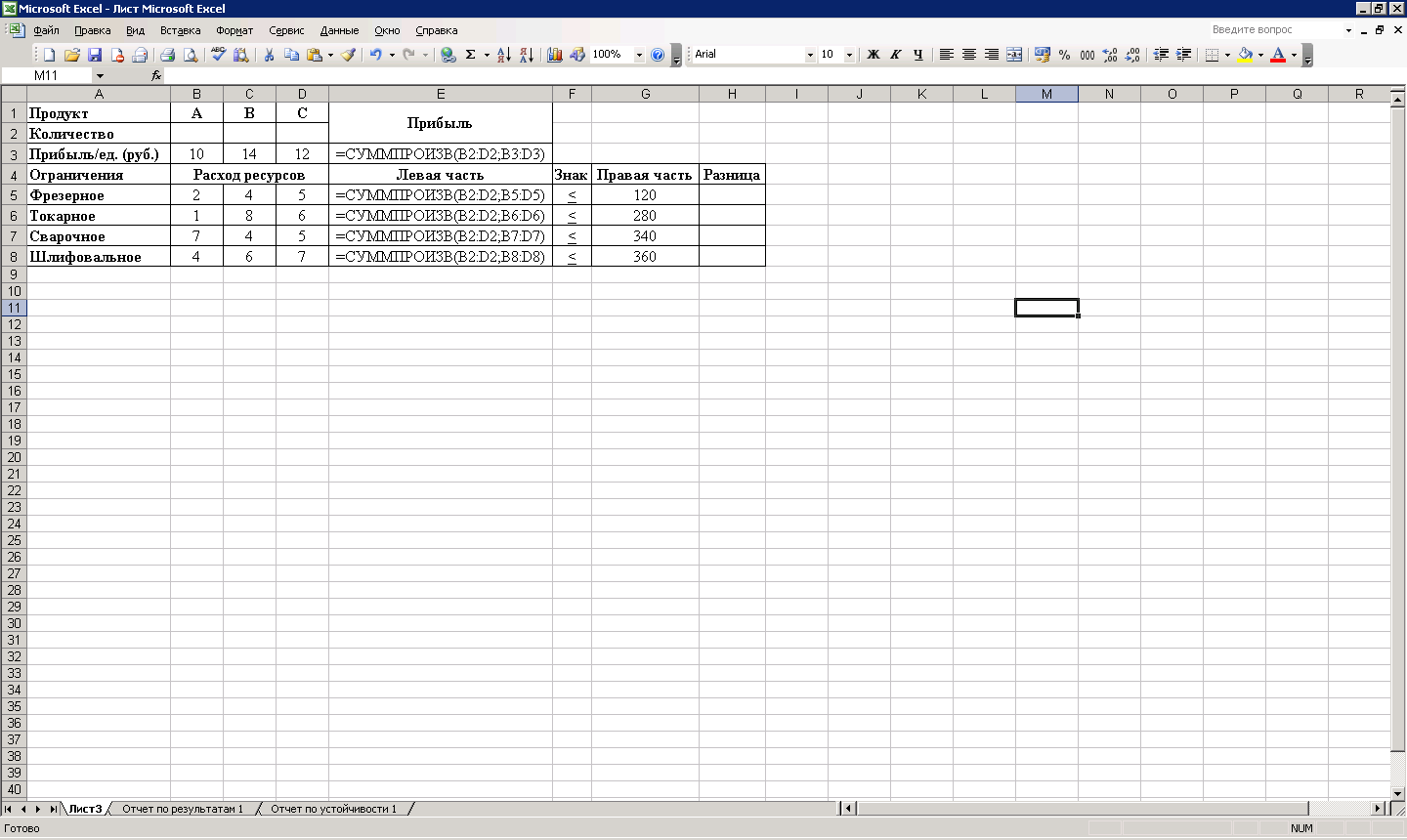
Рис 2.3.3. Зависимость для целевой функции и для левых частей ограничений

5. Запуск «Поиска решения» (Рис. 2.3.4). В диалоговом окне «Поиск решения» заполним три основных параметра: «установить целевую ячейку»,

«Изменяя ячейки» и «Ограничения».

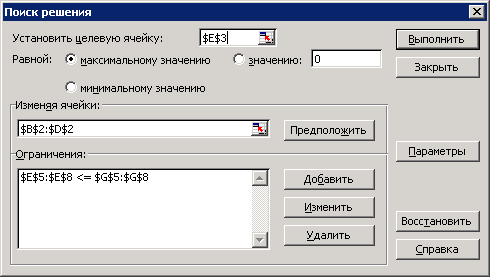
Рис 2.3.4. Поиск решения

5. Ввод параметров «Поиска решения» (Рис. 2.3.5).Устанавливаем флажок «Неотрицательные значения» и флажок «Линейная модель», что обеспечивает применение симплекс-метода.

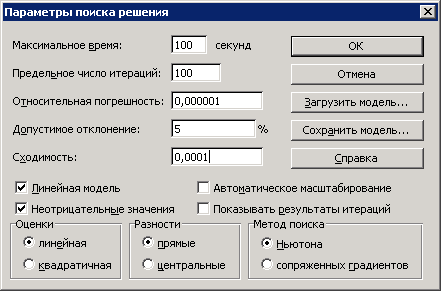
Рис 2.3.5. Параметры поиска решения

6. Найденное решение (Рис 2.3.6). В рассматриваемом примере оптимальное значение переменной . Соответственно, прибыль составляет 552 руб. В данной задаче нет ограничений типа «≥», поэтому все дополнительные переменные являются остаточными. Из таблицы видно, что значения дополнительных переменных для первого и третьего неравенств равны нулю. Это означает, что общий фонд рабочего времени фрезерного и сварочного оборудования потребляется полностью, без остатка. Во втором и четвертом ограничениях значения дополнительных переменных отличны от нуля, то есть неравенства этих ограничений выполняются строго.

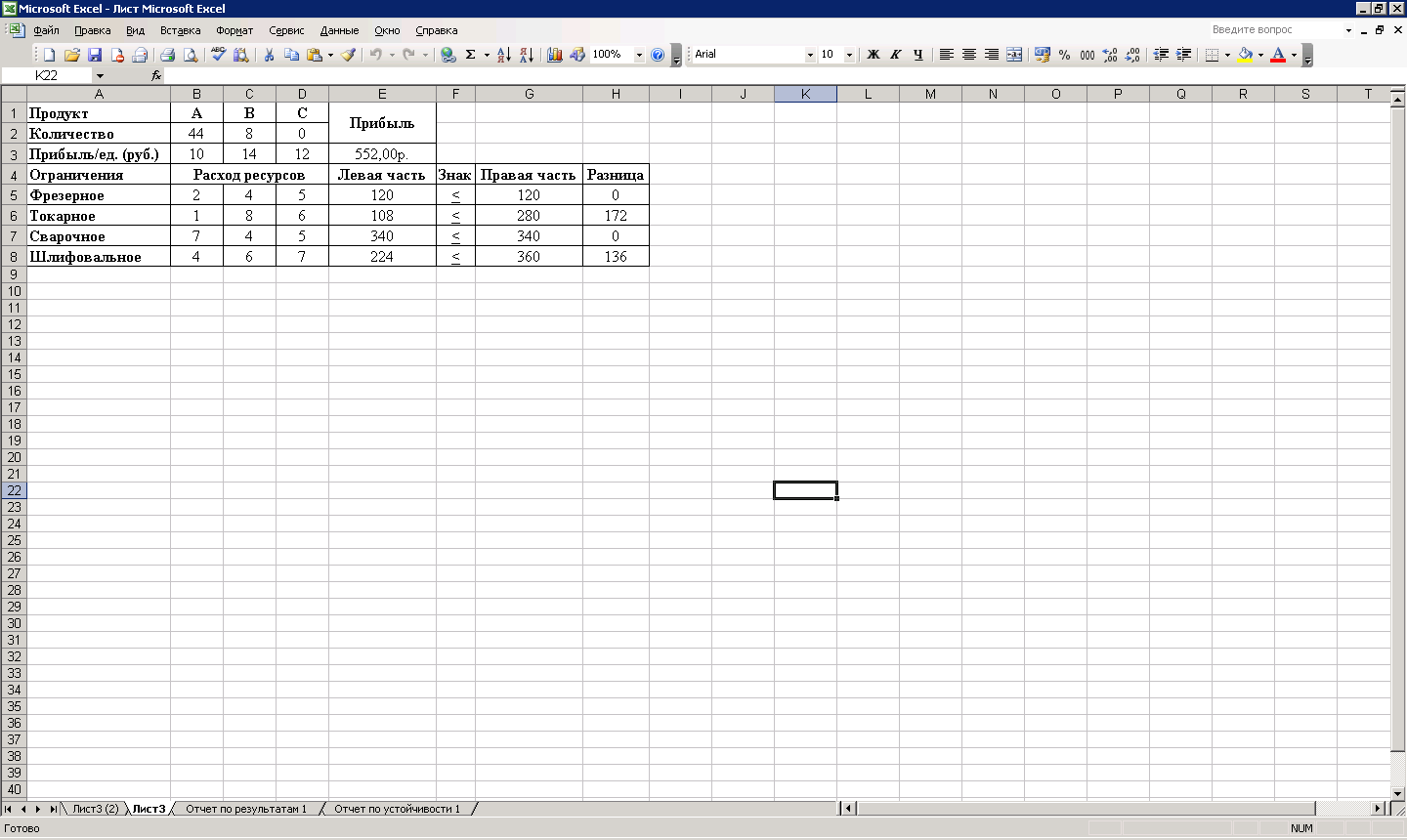
Рис 2.3.6. Найденное решение

7. Отчет по устойчивости содержит информацию, позволяющую провести постоптимальный анализ решения задачи. Цель анализа заключается в определении таких границ изменения исходных данных задачи (коэффициентов целевой функции и правых частей ограничений), при которых ранее найденный оптимальный план сохраняет свою оптимальность и в изменившихся условиях. Отчет состоит из двух таблиц (Рис. 2.3.7).

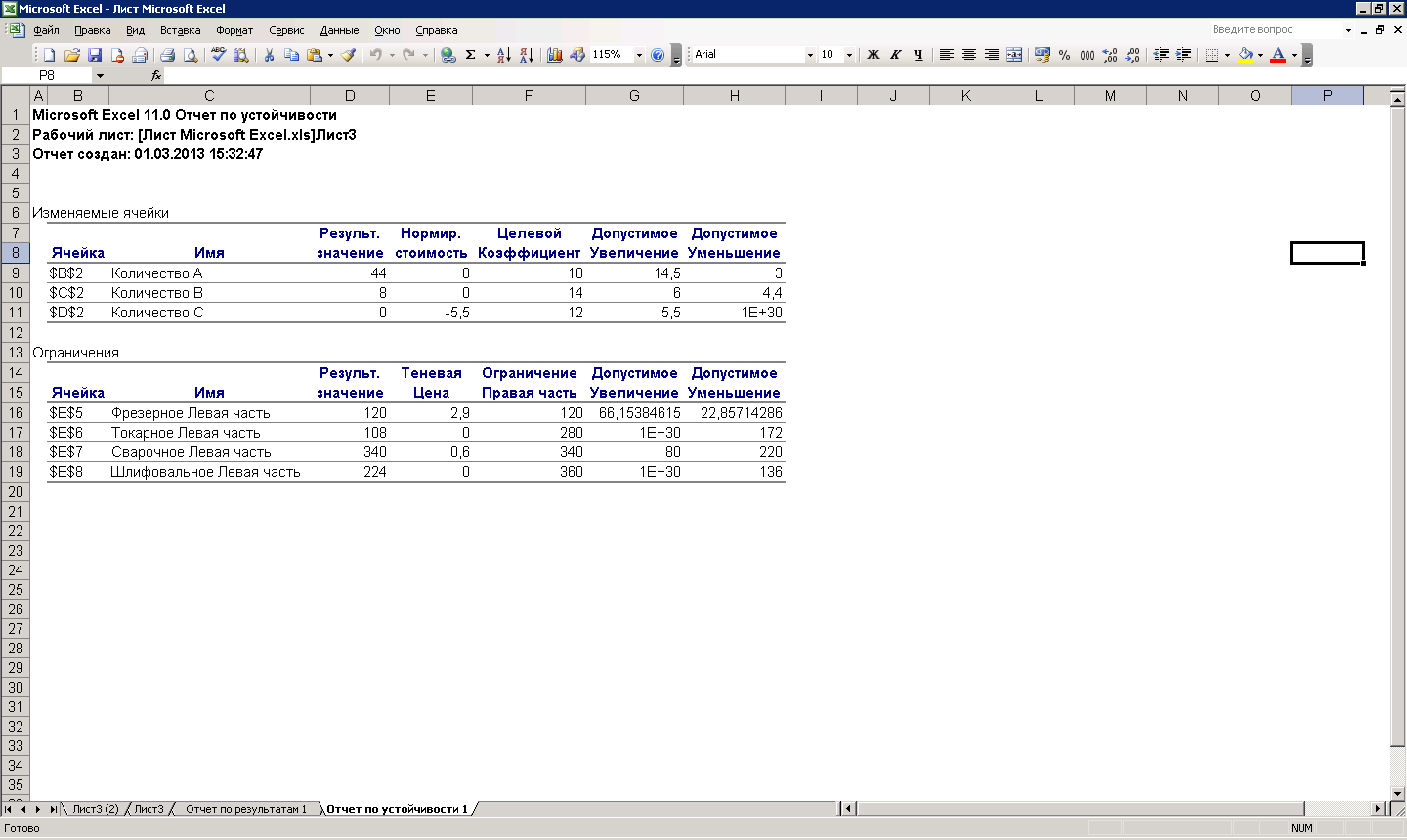
Рис 2.3.7. Отчет по устойчивости

В первой таблице (Изменяемые ячейки) приводится следующая информация о переменных:

- результативное значение – оптимальные значения переменных;

- нормированная стоимость – ее величина равна значению соответствующей симплексной оценки с противоположным знаком. Для невыпускаемой продукции нормированная стоимость показывает, насколько изменится целевая функция при принудительном включении единицы этой продукции в оптимальное решение;

- целевой коэффициент – коэффициенты целевой функции;

- допустимое увеличение/уменьшение – предельные значения приращения коэффициентов целевой функции, которые показывают на сколько можно увеличить и уменьшить каждый целевой коэффициент в отдельности, сохраняя при этом оптимальные значения переменных.

Во второй таблице (Ограничения) приводятся аналогичные значения для ограничений задачи:

- результативное значение – величины использованных ресурсов (левые части ограничений) при оптимальном плане выпуска продукции;

- теневая цена – оптимальные значения двойственных переменных, которые показывают, как изменится целевая функция при изменении соответствующего запаса ресурса на единицу;

- ограничение правая часть – исходные запасы ресурсов (правые части ограничений);

- допустимое увеличение/уменьшение - предельные значения приращения ресурсов (их допустимое увеличение и уменьшение), при которых сохраняется оптимальный план двойственной задачи и базисный набор переменных, входящих в оптимальное решение исходной задачи (ассортимент выпускаемой продукции).

Используем результаты отчета по устойчивости для проведения постоптимального анализа в нашей задаче. Исследуем сначала влияние на оптимальный план изменений коэффициентов целевой функции – цен реализации продукции.

Из первой таблицы следует, что оптимальный план производства изделий не изменится, если первоначальная цена руб. изделия типа А возрастет на 14,5 или уменьшится на 3 руб. Другими словами, условие сохранения оптимального плана при изменении цены изделия А имеет вид: .

Аналогично, условие сохранения оптимального плана при изменении цены изделия В имеет вид: .

Наконец, при изменении цены изделия типа С ранее найденный план останется оптимальным, если исходная цена возрастет не более чем на 5,5. В тоже время любое уменьшение цены не влияет на оптимальный план , т.к. число 1Е+30 равно 10³⁰, т.е. практически является бесконечно большим числом. Таким образом, условие сохранения оптимального плана при изменении цены примет вид . Это означает, что изделие вида С не выгодно выпускать , если цена на них будет не выше 17,5 руб. Если же цена превысит 17,5 руб. за единицу изделия, то план перестанет быть оптимальным и в новом оптимальном решении будет положительным, т.е.производство изделия типа С станет выгодным.

Оценим теперь влияние на оптимальный план изменений правых частей ограничений – запасов общего фонда рабочего времени фрезерного, токарного, сварочного и шлифовального оборудования. Интерпретация данных второй таблицы отчета зависит от того, является ли исследуемое ограничение связанным (активным), или не связанным. Если ограничение не связанное, то соответствующий ему ресурс недефицитен и уменьшение его запаса на величину, не превышающую избытка, не влияет на план выпуска . Тем более не изменяет оптимальный план увеличение запаса недефицитного ресурса, приводя только к возрастанию неизрасходованного остатка. Если же ограничение – связанное, т.е. соответствующий ресурс дефицитен и расходуется полностью, то любое изменение его запаса изменяет объем выпускаемой продукции. Единственное, что можно определить в данном случае, это диапазон изменения запаса ресурса, гарантирующий сохранение прежнего ассортимента выпускаемой продукции.

О дефицитности ресурса можно судить по значению теневой цены из второй таблицы отчета по устойчивости – дефицитный ресурс имеет положительную теневую цену, а недефицитный – нулевую.

Из второй таблицы отчета по устойчивости видим, что общий фонд рабочего времени токарного и шлифовального оборудования избыточны, т.к. их теневая цена . Следовательно, оптимальный план выпуска продукции не изменится, если запас общего фонда рабочего времени уменьшится на величину избытка в 172 и 136 часов соответственно, или увеличится на любое сколь угодно большое число. Таким образом, условие сохранения оптимального плана при изменении объема фонда общего фонда рабочего времени на токарном и шлифовальном станках имеет вид: .

В первой и третьей строках второй таблицы отчета по устойчивости теневые цены положительны, значит общий фонд рабочего времени для фрезерного и сварочного оборудования дефицитны – при оптимальных объемах производства используются полностью. Следовательно, любое изменение их количества приведет к изменению оптимального плана . В этом случае числа из столбцов «Допустимое увеличение» и «Допустимое уменьшение» дают границы изменения запасов ресурса, обеспечивающие сохранение прежнего состава базисных (положительных) переменных оптимального плана – ассортимента выпуска продукции.

Итак, при изменении количества часов фрезерного оборудования в пределах ассортимент используемого выпуска не изменится.

Аналогично, если количества часов сварочного оборудования будет находится в пределах , то ассортимент выпуска не изменится.

Это означает, что если запасы ресурсов изменяются в указанных пределах, то оптимальному плану по-прежнему надо выпускать только изделия типа А и В, но уже в новых объемах.

Как видно из второй таблицы отчета по устойчивости, теневая цена фрезерного оборудования , а сварочного оборудования .