Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Санкт-Петербургский государственный политехнический университет»
Факультет экономики и менеджмента
Кафедра предпринимательства и коммерции
Курсовая работа
по дисциплине «Математические методы в экономике»
на тему «Методы оптимальных решений»
Выполнил студент группы в3077/20
_______________ К.В. Фролова
Принял доцент, к.э.н
________________ Д.В. Тихонов
Оценка: _______________
«_____» _______________ 2013 года
Санкт-Петербург
2013
Фролова К.В. Методы оптимальных решений : Курсовая работа по дисциплине «Математические методы в экономике». – СПб.: СПбГПУ, 2013. – 18 с, рис. – 8, табл. – 1.
МАТЕМАТИЧЕСКИЕ МЕТОДЫ, МЕТОД ВЕТВЕЙ И ГРАНИЦ, ЗАДАЧА ЛИНЕЙНОГО ПРОГРАМИРОВАНИЯ, ОТЧЕТ ПО УСТОЙЧИВОСТИ
Теоретическая часть курсовой работы содержит описание метода ветвей и границ. Описание включает в себя общее описание метода, условия и варианты его применения, математическую запись, пример задачи.
Практическая часть включает в себя решение задачи линейного программирования с помощью Microsoft Excel.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ 4
1. МЕТОД ВЕТВЕЙ И ГРАНИЦ 5
1.1. Описание задачи целочисленного программирования 5
1.2. Описание метода ветвей и границ 5
1.3. Алгоритм действия метода ветвей и границ 6
1.4. Общий алгоритм решения задач с помощью метода границ и ветвей, его суть 7
1.5. Пример использования метода ветвей и границ 8
2. ТЕХНОЛОГИЯ РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ПОМОЩЬЮ MICROSOFT EXCEL 10
2.1. Условие задачи 10
2.2. Математическая модель задачи 10
2.3. Решение задачи с помощью Microsoft Excel 11
ЗАКЛЮЧЕНИЕ 17
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 18
Введение
Теоретическая часть курсовой работы содержит описание метода ветвей и границ. Описание включает в себя общее описание метода, условия и варианты его применения, математическую запись, пример задачи.
Данная тема является чрезвычайно актуальной, ведь метод ветвей и границ в связи с простотой сущности алгоритма используется при работе на некоторых ЭВМ, а решения задач календарного планирования всегда востребованы как в экономической отрасли, так и других, смежных с ней.
Практическая часть содержит задачу, которую нужно решить на компьютере с помощью программы Excel и выполнить анализ чувствительности полученного решения. Решая задачу, необходимо выполнить следующее:
1. Ввести обозначения для переменных.
2. С помощью этих обозначения записать целевую функцию и ограничения модели.
3. Оформить модель в виде электронной таблицы Excel.
4. Оформить модель с помощью средства Поиска решения и получить отчет по устойчивости.
5. Объяснить, какой экономический смысл несут значения в отчете по устойчивости.
6. Выписать все интервалы оптимальности и устойчивости и пояснить их экономический смысл.
1. Метод ветвей и границ
1.1. Описание задачи целочисленного программирования
По смыслу значительной части экономических задач, относятся к задачам линейного программирования, компоненты решения должны выражаться в целых числах, т.е. быть целочисленными. К ним относятся, например, задачи, в которых переменные означают количество единиц неделимой продукции, число станков при загрузке оборудования, число судов при распределениях по линиям, число турбин в энергосистеме, число вычислительных машин в управляющем комплексе и многие другие.
Задача линейного целочисленного программирования формируется следующим образом: найти такое решение (план) X = (x1,x2,...,xn), при котором линейная функция
(1.1)
принимает максимальное или минимальное значение при ограничениях:
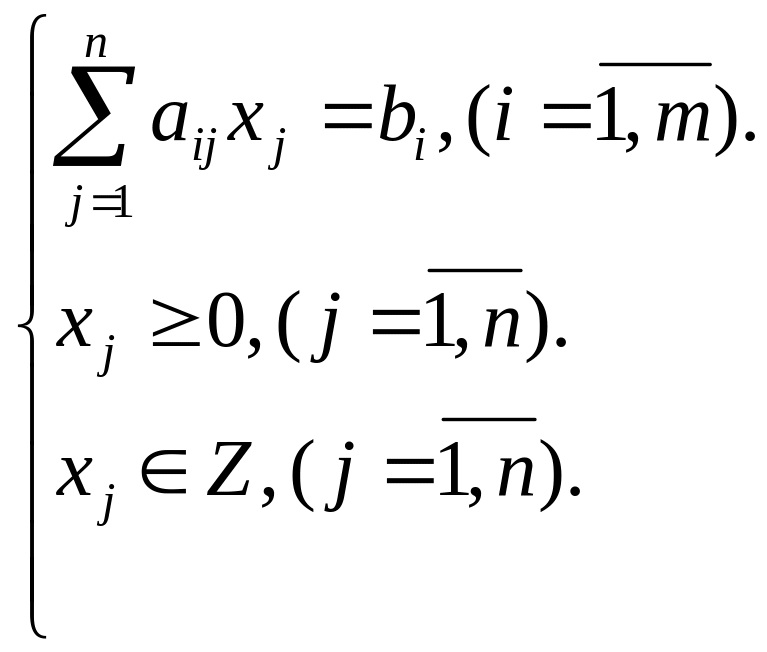
(1.2)
(1.3)
(1.4)