Асиметричні крипто системи

Необоротні функції

Асиметричні крипто системи базуються на існуванні необоротних функцій, тобто функції які достатньо легко обчислюються, однак знаходження для них оберненої функції і надзвичайно складної в обчислювальному плані задач. Прикладами таких функцій є задача факторизації (множення цілих чисел достатньо проста задача, розкладання числа на множники складна задача), задача дискретного логарифмування (y=a^x mod n, знаходження n є складною задачею).

Теоретичного доведення існування оборотної функції на сьогодні не має, тому це є слабким місцем ассиметричних систем, тому в практиці під необоротністю розуміють не можливість обчислення зворотної функції за допомогою сучасних обчислювальних засобів за прийнятний час. Розробники комерційних реалізацій криптосистем намагаються використати односторонні функції з потаємним ходом, тобто такі функції для яких відомі простий алгоритм обернення, але для обмеженого кола людей.

Деякі відомості з теорії чисел

Модулярна арифметика

Якщо a b n цілі додатні числа причому n<>0 b<n, а порівняне в за модулем n. Порівняння справедливе якщо, залишки від ділення а на n і b на n однакові.

Число b називаеться лишком (вычет) числа а за модулем n. Операція знаходження лишка а mod n = b. Набір цілих чисел від 0 до n-1 називаеться повним набором лишків по модулю n.

Операція приведення за модулем має наступні властивості:

Адитивність

Мультиплікативність

Дистрибутивність a(b+c))mod n = ((a*b)mod n + (a*c)mod n)mod n

У сучасній криптографії, яка працює з великими числами і трудомісткими операціями модулярна арифметка використовується дуже широко бо:

1 забезпечує необоротність обчислень

2 дозволяє в процесі обчислень значно зменшити діапазон проміжних величин

Хеш функції

Хеш функція йе алгоритм який перетворює рядок символів довільної довжини на рядок символів фіксованої довжини. В системах захисту інформації хеш функції широко використовуються для перевірки цілістності повідомлення, забезпечення справжньості цифрових підписів, збереження паролів тощо.

Най постішим прикладом хеш фукції є додавання за модулем 2 всіх символів повідомлення (у двійковому вигляді).

Ця функція для бкдь якого довжини аргумента M буде видавати результат довжиною 1. Якщо потрібно щоб результат хешування мав довжину l, то потрібно початкові блоки розбити по довжині l і додати за модулем 2.

До хеш функції пред'являються 3 основні вимоги:

1 стійкість в смислі обернення (для даного хешу h(M) повинно бути дуже важко або неможливо знайти значення M);

2 стійкість в смислі колізій (для данного аргумента M повинно дуже важко або неможливо знайти інший аргумент M' такий щоб h(M')=h(M));

3 хеш функція повинна достатньо швидко обчислюватися для забезпечення можливості її практичного застосування.

Наведена в якості прикладу хеш функція володіє першою і другою властивістю, але не володіє третьою тобто не годиться для практичного використання.

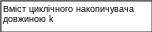
Оеальні хеш функції значно складніші, однак всі вони мають практично один і той самий алгоритм.

Основними параметрами алгоритму є:

1 правило нормалізації початкового повідомлення (приведення до деякої стандортної довжини);

2 алгоритм функціонального перетворення (кроова функція);

3 розрядність результату зешування.

Хеш алгоритм md5 (message digest)

1 До початкового повідомлення дописують 1 а потім таку кількість нулів щоб довжина повідомлення l була порівняно з 448(mod 512). Після чого дописують 64 розрядне представлення початкового повідомлення (якщо довжина повідомлення перевищує 2^64 - 1 то дописують до 64. В результаті після нормалізації довжина повідомдення стає кратним 512.

2 ініціалізація буферу виконується 4-ма 32 розрядними константами A B C D

A = 0 1 2 3 4 5 6 7

B = 8 9 a b c d e f

C = fedcba98

D = 76543210

Використовується 4 функції

F1 (X,Y

Повідомлення розбиветься на блоки довжиною по 32 розряди кожний з яких піддається 4 циклам перетворення з 16 оперціями виклику.