Дробно - линейная функция

а, b, с, d - постоянные, причем (иначе мы имели бы линейную функцию) и (иначе произошло бы сокращение и мы получили бы постоянную функцию).

l a. В начале рассмотрим функцию

Функция определена всюду, кроме х = 0, то есть область определения интервалы .

Область значения также интервалы .

Функция нечетная, так как

Функция убывающая (при к > 0) и возрастающая (при k < 0) на интервалах .

Функция неограниченная.

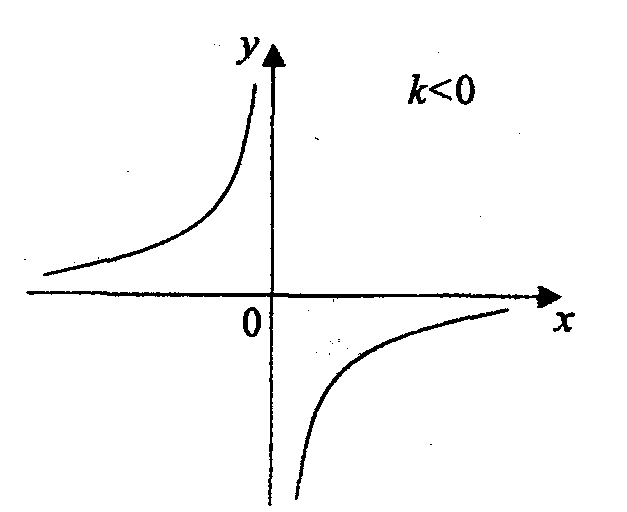
Полученная кривая называется гиперболой.

1б. Общий случай

Полагая получаем

С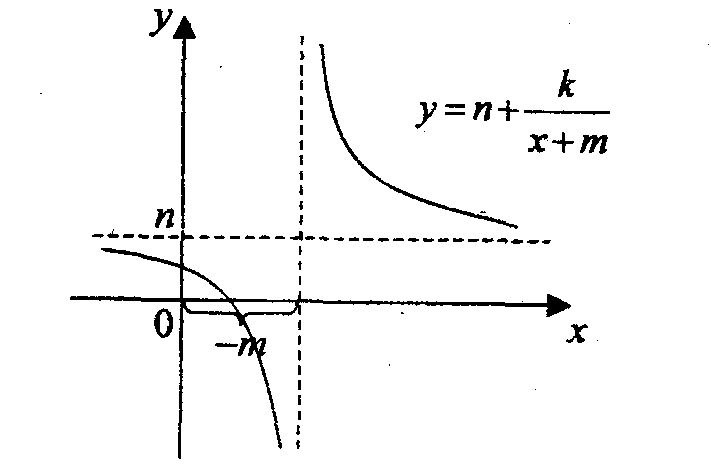 ледовательно график функции легко получить из графика функции с помощью сдвига на - т вдоль оси Ох и на n единиц вдоль оси Оу.

Свойства функции получаем из свойств функции

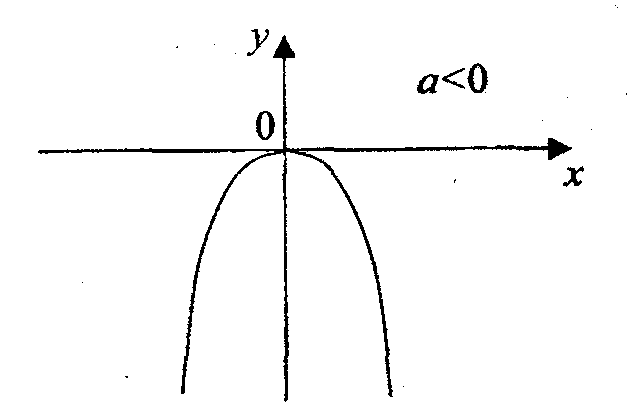
Квадратный трехчлен ( , иначе функция линейная).

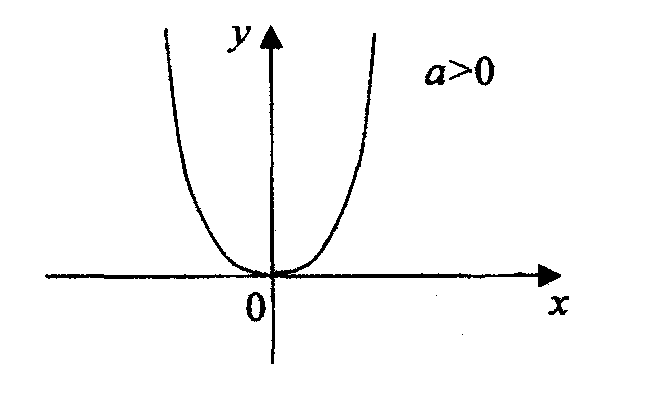
1а. Квадратная функция у=ах².

Функция определена при всех х.

Область значения неотрицательные числа (при a > 0) неположительные числа при а < 0.

- функция четная

- функция не является периодической

- функция ограничена снизу при а > 0, ограничена сверху при а < 0

- функция убывает на интервале ( ; 0) при a > 0

возрастает при a < 0

возрастает на интервале (0; ) при а > 0

убывает при а < 0.

1б. Общий случай .

Получим : Полагая получим

График данной функции получается из графика функции у = ах²

сдвигом на - т по оси Ох и сдвигом на п по оси Оу.

Степенная функция у = хⁿ.

1а. Рассмотрим случай n = 2k.

Функция определена на всей числовой оси.

Функция четная, так как

Функция не является периодической.

На интервале (- ; 0) функция убывает, на интервале (0; + ) функция возрастает.

Функция ограничена снизу.

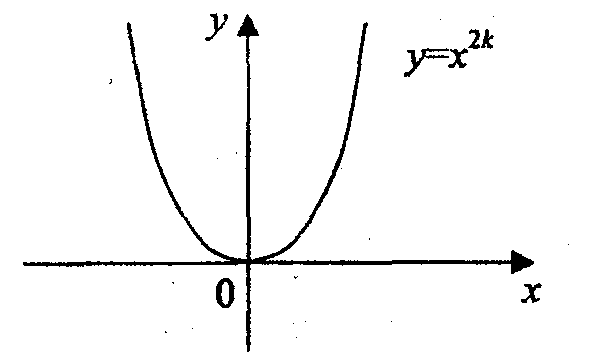
1б. Случай n = 2k + 1, y = x^2к+1 .

Функция определена всюду.

Функция нечетная.

Функция не является периодической. Возрастает на всей числовой оси.

Функция не ограничена.

Преобразование графиков

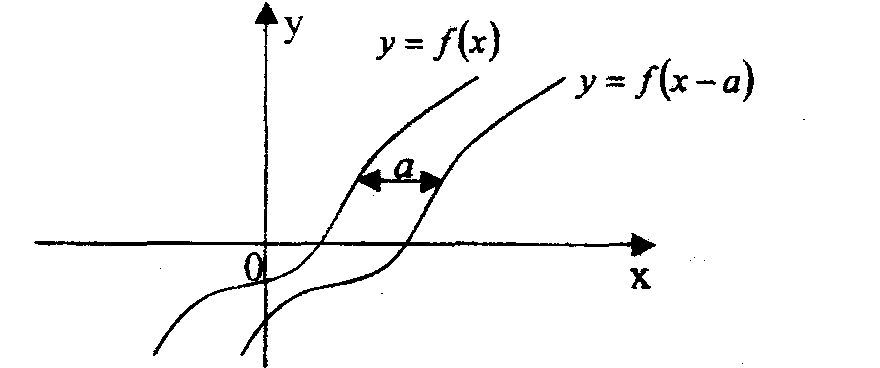
Правило 1. График функции у = f(x - а) (у = f(x + а)) получается из графика функции у = f(x) сдвигом последнего вдоль оси Ох на а единиц вправо (влево), а > 0.

Правило 2. График функции y = f(x)+b (у = f(x)- b) получается из графика функции у = f(x) сдвигом вдоль оси Oу на b единиц в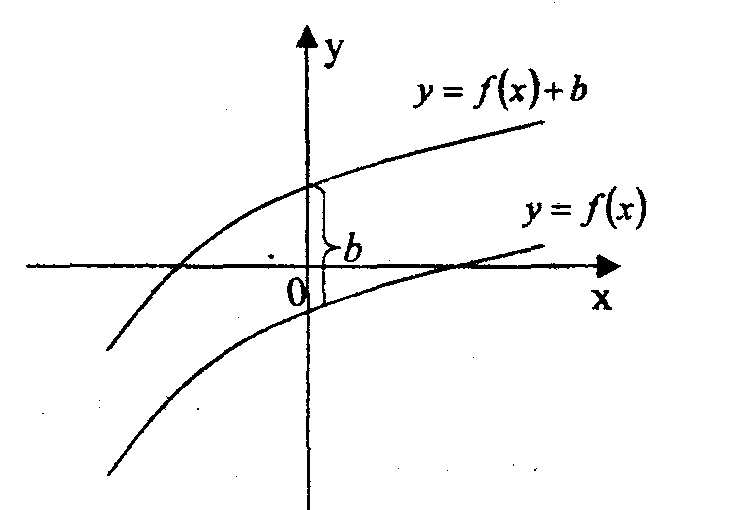 верх (вниз), b > 0.

Правило 3. График функции y = k f(x), где k > 0, получается из графика y = f(x) растягиванием последнего вдоль оси Оу с коэффициентами k.

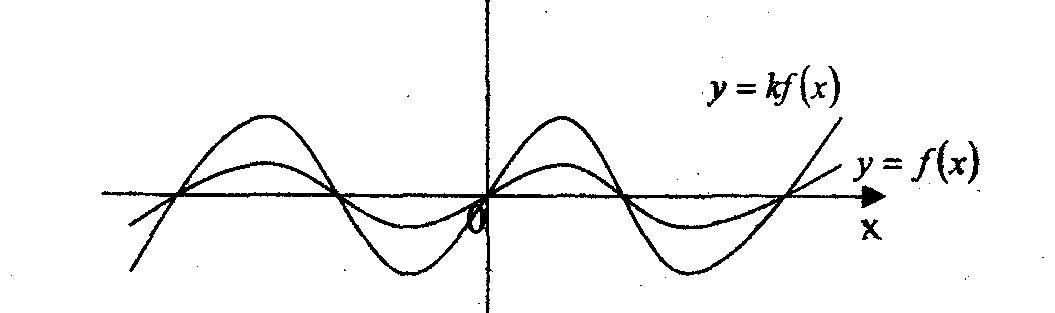
Правило 4. График функции у = f(ax), где а > 0, получается из графика у = f(x) сжатием последнего вдоль оси Ох с коэффициентом, равным а.

Правило 5. График функции у = f(- х) получается из графика функции у = f(x) симметричным отображением последнего относительно оси Oу.

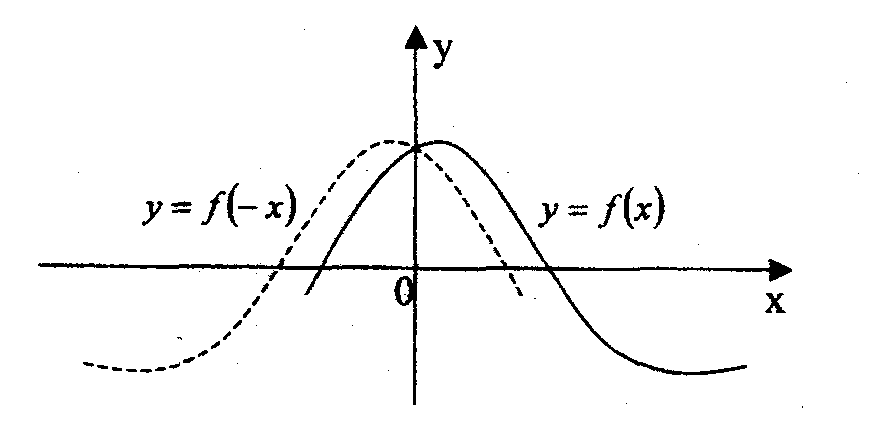
Правило 6. График функции у = - f(x) получается из графика функции у = f(x) симметричным отображением последнего относительно оси Ox.

Правило 7. График функции y = f(|x|) совпадает с графиком функции f(x) в правой полуплоскости ( ), а в левой полуплоскости (х < 0) симметричен этой части графика относительно оси Оу .

Правило 8. График функции у = |f(х)| совпадает с графиком функции у = f(х) для тех участков оси Ох, где , и является симметричным отображением его относительно оси Ох для тех участков,

где f(x) < 0.