7. Экономический смысл основных и дополнительных переменных в канонической форме задачи об оптимальном использовании ограниченных ресурсов

П ланом, или допустимым решением, КЗЛП называется вектор =(х_1,х_2,…,х_n), удовлетворяющий условиям. Если все компоненты базисного решения системы ограничений КЗЛП неотрицательны, то такое решение называется опорным решением или опорным планом. Число положительных компонент опорного плана не может превышать m. Опорный план называется невырожденным, если он содержит m положительных компонент, в противном случае он называется вырожденным. Оптимальным планом или оптимальным решений ЗЛП называется план, доставляющий наибольшее (наименьшее) значение линейной функции f ()= с₁х₁+с₂х₂+…+с_nх_n

max (min). Множество всех планов ЗЛП ( если они сущ) явл выпуклым многогранником. Каждой угловой (крайней) точке многогранника решений соответствует опорный план (неотрицательные базисные решения системы уравнений КЗЛП). Каждый опорный план определяется системой m линейно независимых векторов, сод в данной системе из n векторов ₁, ₂,..,_n. Если сущ оптимальный план, то сущ такая угловая точка многогранника решений, в которой линейная функция достигает своего наибольшего (наименьшего) значения. Для отыскания оптимального плана достаточно исследовать только опорные планы. Верхняя граница количества опорных планов, сод в задаче, определяется кол-вом сочетаний .

8. Решение систем линейных уравнений методом Жордана - Гаусса. Общее решение, частное, базисные и опорные решения слу

Алгоритм решения систем уравнений методом Жордана -Гаусса состоит из ряда однотипных шагов, на каждом из которых производятся действия в следующем порядке:

1. Проверяется, не является ли система несовместной. Если система содержит противоречивое уравнение, то она несовместна.

2. Проверяется возможность сокращения числа уравнений. Если в системе содержится тривиальное уравнение, его вычеркивают.

3. Если система уравнений является разрешенной, то записывают общее решение системы и если необходимо - частные решения.

4. Если система не является разрешенной, то в уравнении, не содержащем разрешенной неизвестной, выбирают разрешающий элемент и производят преобразование Жордана с этим элементом.

5. Далее заново переходят к пункту 1

Пример Решить систему уравнений методом Жордана-Гаусса.

Найти: два общих и два соответствующих базисных решения

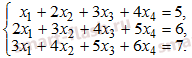
Решение:

Вычисления приведены в нижеследующей таблице:

Справа от таблицы изображены действия над уравнениями. Стрелками показано к какому уравнению прибавляется уравнение с разрешающим элементом, умноженное на подходящий множитель.

В первых трех строках таблицы помещены коэффициенты при неизвестных и правые части исходной системы. Результаты первого преобразования Жордана с разрешающим элементом равным единице приведены в строках 4, 5, 6. Результаты второго преобразования Жордана с разрешающим элементом равным (-1) приведены в строках 7, 8, 9. Так как третье уравнение является тривиальным, то его можно не учитывать.

Равносильная система с разрешенными неизвестными Х₁ и Х₂ имеет вид: Теперь можем записать Общее решение:

Приравниваем свободные переменные Х₃ и Х₄ нулю и получаем: Х₁ = -3+0+0 = -3, Х₂ = 4-2*0-3*0 = 4.

Базисное решение: Х_б1 = (-3,4,0,0)

Для того чтобы найти второе общее и соответствующее ему базисное решение, в полученной разрешенной системе в каком-либо уравнении необходимо выбрать какой-либо другой разрешающий элемент. (дело в том, что линейное уравнение может содержать несколько общих и базисных решений). Если разрешенная система уравнений, равносильная исходной системе содержит n неизвестных и m уравнений, то число общих и соответствующих базисных решений исходной системы равно числу сочетаний n и m. Количество сочетаний можно вычислить по формуле:

В нашем случае выбран разрешающий элемент (-1) в первом уравнении при x₃ (строка 7). Далее  производим преобразование Жордана. Получаем новую разрешенную систему (строки 10,11) c новыми разрешенными неизвестными Х2 и Х3:

Записываем второе общее решение:

И соответствующее ему базисное решение: Х_б2= (0, -2, 3, 0)

Ответы:

Общее решение:

Базисное решение: Х_б1 = (-3,4,0,0)

Общее решение:

Базисное решение: Х_б2= (0, -2, 3, 0)