17. Запишіть як виражається середня квадратична швидкість молекул газу.

З графіка функціі видно, що вона має максимум при , тобто швидкість молекули мають частіше, ніж іншого значення і з цієї причини її називають найбільш ймовірною. Наприклад, швидкість, що вдвічі більша за найбільш ймовірну зустрічається приблизно в 0,2 рази рідше, ніж найбільш ймовірна. Величина найбільш ймовірної швидкості залежить від температури і природи газу

= . (2.15)

Середня квадратична швидкість молекул знаходиться за формулою

= , (2.16)

а

Рис. 2-3.

середня арифметична швидкість молекул

Рис. 2.3

= . (2.17)

Якщо вираз для найбільш ймовірної швидкості (2.15) підставимо в рівняння (2.14), то отримаємо в іншому вигляді функцію розподілу молекул за швидкостями, яка ще називається функцією Максвелла – Больцмана:

. (2.18)

При врахуванні, що кінетична енергія молекули це –

,

отримаємо з (2.18) рівняння розподілу кінетичної енергії молекул:

.

17. Дайте визначення найбільш ймовірної швидкості молекул газу.

З графіка функціі видно, що вона має максимум при , тобто швидкість молекули мають частіше, ніж іншого значення і з цієї причини її називають найбільш ймовірною. Наприклад, швидкість, що вдвічі більша за найбільш ймовірну зустрічається приблизно в 0,2 рази рідше, ніж найбільш ймовірна. Величина найбільш ймовірної швидкості залежить від температури і природи газу

= . (2.15)

Середня квадратична швидкість молекул знаходиться за формулою

= , (2.16)

а

Рис. 2-3.

середня арифметична швидкість молекул

Рис. 2.3

= . (2.17)

Якщо вираз для найбільш ймовірної швидкості (2.15) підставимо в рівняння (2.14), то отримаємо в іншому вигляді функцію розподілу молекул за швидкостями, яка ще називається функцією Максвелла – Больцмана:

. (2.18)

При врахуванні, що кінетична енергія молекули це –

,

отримаємо з (2.18) рівняння розподілу кінетичної енергії молекул:

.

17. Що впливає на число молекул газу, що ударяються за одиницю часу в одиницю поверхні стінки ємності?

У вакуумній техніці в багатьох випадках необхідно визначити кількість молекул газу, що проникнуть за одиницю часу через якийсь отвір у стінці ємності, в якій знаходиться газ. Для цього необхідно знати кількість молекул газу, що ударяються за одиницю часу в одиницю площини стінки ємності, в якій знаходиться газ.

Р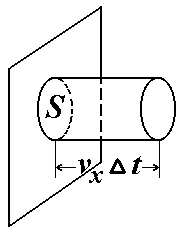 озглянемо циліндр з площею основи S і довжиною t, що дорівнює відстані, яку пробігає одна молекула за проміжок часу t, маючи на увазі, що вона ударяється в стінку (основу S). Тоді число молекул, що ударяється в основу S дорівнюватиме

.

Д

Рис. 3.1

війка в знаменнику показує, що тільки половина молекул спрямовується до кожної основи.

Оскільки , то за одиницю часу

Замінимо середню квадратичну швидкість на середню арифметичну, тоді отримаємо

.

Якщо враховувати, що не всі молекули спрямляються до основи перпендикулярно, а частина буде ударятися під всілякими кутами, то необхідно підкореневий вираз замінити на одиницю і остаточно отримаємо число молекул газу, що ударяються за одиницю часу в одиницю площини стінки

. (3.1)

Використовуючи рівняння Больцмана і формулу (2.20) матимемо, що ця кількість прямопропорційно залежить від тиску

(3.2)

і маса молекул газу, що ударяються за одиницю часу у одиницю поверхні стінки ємності, в якій знаходиться газ буде дорівнювати

.