2 Методи розв’язування систем лінійних рівнянь
2.1 Метод Крамера
Систему двох нормальних рівнянь можна розв'язати, користуючись методом Крамера. Нехай, наприклад, після обчислення всіх необхідних сум система нормальних рівнянь (1) набуває вигляду:
(9)
де
До аналогічної системи зводяться і системи (2), (4), (6), (7).
Для
системи (9) обчислимо головний визначник
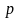та допоміжні визначники
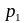і
:
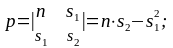
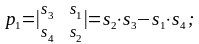
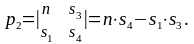
За методом Крамера розв'язок системи рівнянь буде наступним:
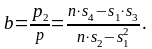
Аналогічно розв’язуються системи трьох і більше лінійних рівнянь.
Нехай, наприклад, після обчислення всіх необхідних сум система трьох нормальних рівнянь (8) набуває вигляду:
(10)
де
.
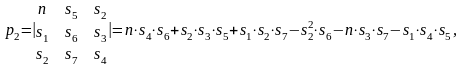
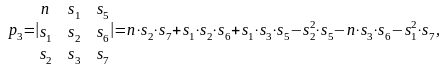
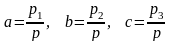2.2 Метод оберненої матриці
Метод оберненої матриці полягає в наступному. Запишемо систему (10) у „матричній” формі:
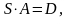(11)
де
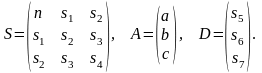
Помноживши
рівняння (11) на матрицю
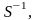обернену до матриці
отримаємо
шуканий вектор
який і є розв’язком системи (11), а, отже,
і системи (10):
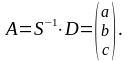(12)
2.3 Розв’язування систем лінійних рівнянь на пк
Розглянемо методи розв’язування систем лінійних рівнянь засобами мови C#, MS Excel. Реалізація методу Крамера на ПК будь-якими програмними засобами досить проста, оскільки всі обчислення зводяться до звичайних арифметичних дій. Що стосується методу оберненої матриці, то ключовим для його реалізації є обчислення матриці, оберненої до матриці коефіцієнтів при невідомих. Метод оберненої матриці доцільніше застосовувати при розв’язуванні систем лінійних рівнянь в середовищі MS Excel, оскільки в цих програмах є „вбудовані” засоби обчислення оберненої матриці. Так, наприклад, нехай потрібно розв’язати систему рівнянь (11).
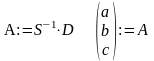
MS
Excel
має стандартні функції МОБР (обчислення
оберненої матриці) та МУМНОЖ (множення
двох матриць), за допомогою яких розв’язок
системи лінійних рівнянь можна записати
у вигляді однієї формули. Так, якщо
елементи матриці
записати в діапазоні А1:С3, а елементи
стовпця
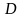– в діапазоні D1:D3,
то
ця формула матиме вигляд:
=МУМНОЖ(МОБР(А1:С3);D1:D3).
3 Побудова емпіричної формули
3.1 Вибір двох апроксимуючих функцій
Мій вибір двох функцій ґрунтувався виходячи з графіку 3.1 – Графіку заданої залежності. Порівняємо наш графік з іншими шістьма графіками заданих функцій.
Найбільше для нашого графіку підходять дві функції: лінійна функція і степенева функція.
Рисунок 3.1 – Графік заданої залежності
3.1.1 Лінійна функція
Згідно з методом найменших квадратів функція вважається кращим наближенням до , якщо для неї сума квадратів відхилень має найменше значення порівняно з іншими функціями, з яких вибирається наближення. А лінійна функція є однією з тих самих, що дають таке значення. І вона має ще ряд переваг, а саме:
Простота лінійної функції у використанні і відставлені даних.
Розв'язки при використанні лінійної функції є достатньо точними(В цьому я переконався при створенні програми на C#).
Графік лінійної функції можна легко прослідкувати.