База правил

∆l/∆l'	Большое пол.	Среднее пол.	Малое пол.	Нулевое	Отрицат
Большое пол.	MAX	HI	LOW	MIN	MIN
Среднее пол.	MAX	VHI	MID	MIN	MIN
Нулевое	MAX	MAX	HI	LOW	MIN
Отрицат.	MAX	MAX	MAX	MID	MIN

Значения (MAX, MIN...) - лингвистические переменные, на раннее полученных экспериментальных данных было посчитано достаточным наличие 5ти лингвистических переменных для рассогласования и 4х для производной рассогласования, они выбраны для изменения оборотов двигателя и изменения подачи топлива, так же за раннее были выбраны для них функции принадлежности они отображают входные параметры на множестве от -1..8 (значения множества тоже были выбраны исходя из экспериментальных данных)

В данном случае есть некая входная переменная и рассогласование, и с помощью ф-ций принадлежности каждой из лингвистических переменных (термов) ставится соответствие входным значениям четким - нечеткая лингвистическая переменная. Область от -1..8 - универсальное множество, а все нечеткие множества (лингвистич. переменные) описывают на этом множестве степень принадлежности конкретного числа к определенному терму.

В соответствии с ранее полученными экспериментальными данными получаем график:

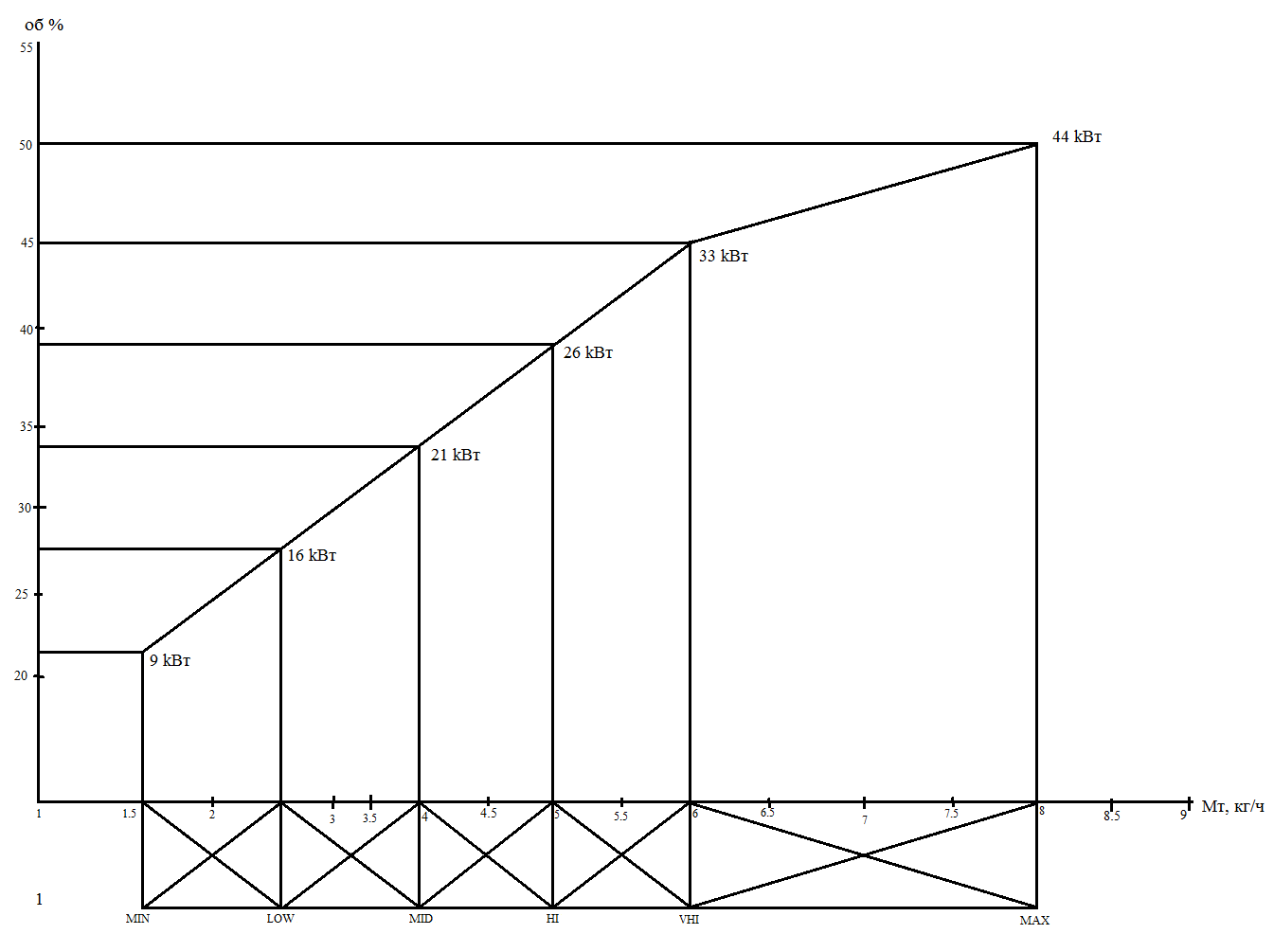
Рисунок 15. Зависимость мощности от оборотов двигателя (шнека) к подаче топлива - кг/ч

Из графика ясно, что мощность системы возрастает с увеличением оборотов двигателя.

По виду график выглядит как линейный, но на самом деле он таковым не является.

Получим другую зависимость.

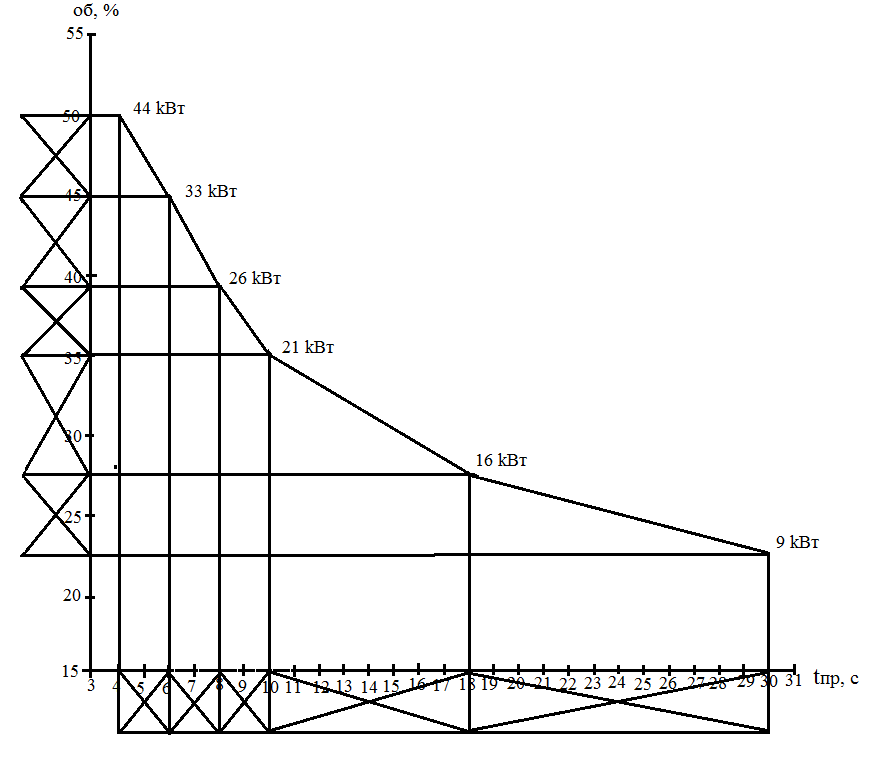
Рисунок 16. Зависимость мощности системы от времени простоя двигателя (шнека)

На графике изображены не все значения мощности и оборотов, реально их большее количество, и соответственно большее количество точек для которых можно построить значения мощности и оборотов, если их все построить, то получается трех - мерное изображение т.е. меняющаяся в мощности - фигура (рис.)

Моделирование поверхности нечеткого ПД - регулятора в среде MATLAB

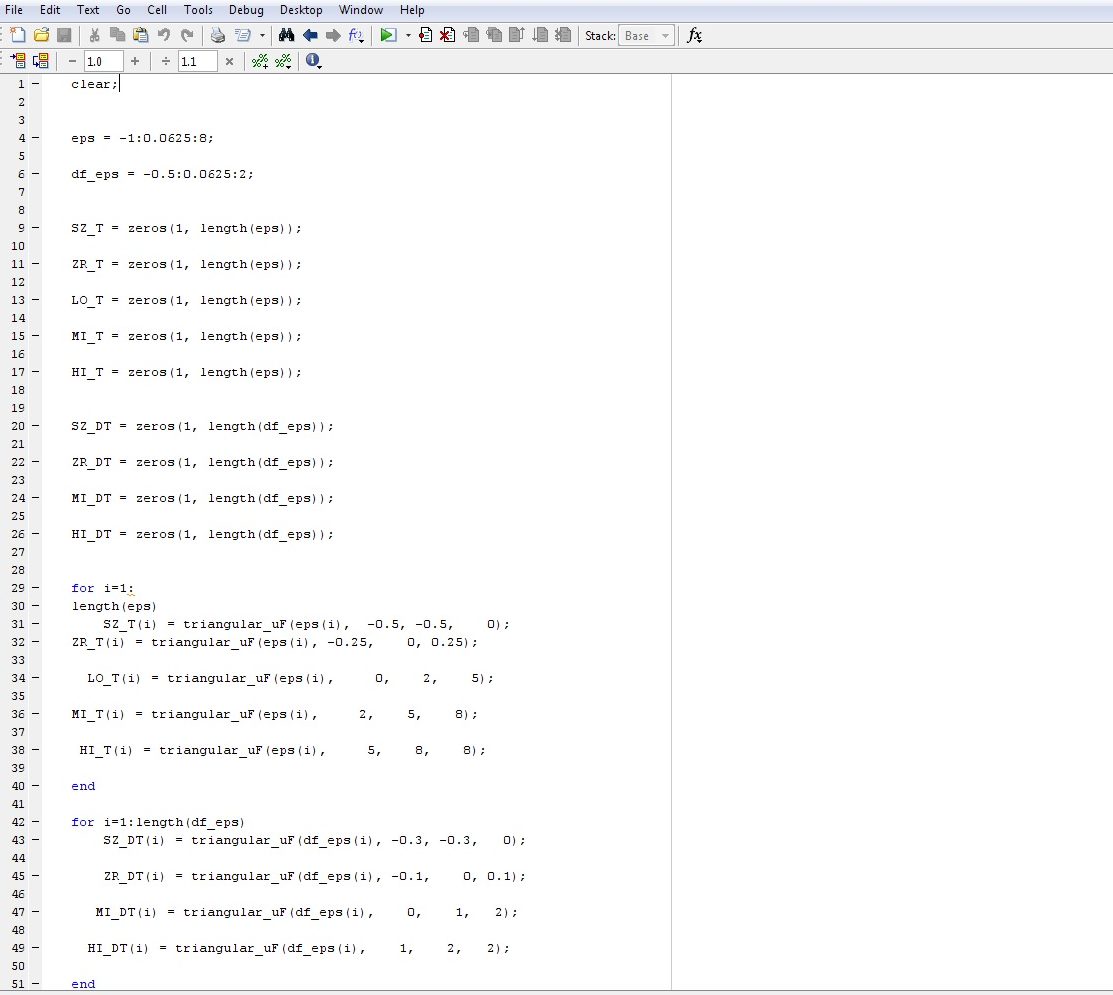
SZ_T =zeros,(1,length(eps));

ZP_T = zeros,(1,length (eps));

LO_T =zeros,(1,length(eps));

MI_T = zeros,(1,length(eps));

HI_T =zeros,(1,lengch(eps));

SZ_DT = zeros,(1,length(df_eps));

ZR_DT= zeros,(1,length(df_eps));

HI_DT = zeros,(1,length(df_eps));

HI_DT = zeros,(1,length(df_eps));

Выше приведены 5 лингвистических переменных для одного входа и 4е для другого (которые образуют 20 правил), этот набор переменных называют "Проклятием размерности" - т.е. чем больше лингвистических переменных тем больше количество правил , которые в итоге очень сложно обработать, следовательно система основанная на нечеткой логике с ростом входных переменных растет экспоненциально. В данном случае у нас имеется небольшое количество правил которые не с затруднением можно обработать и нас понятие - "Проклятие размерности" не касается.

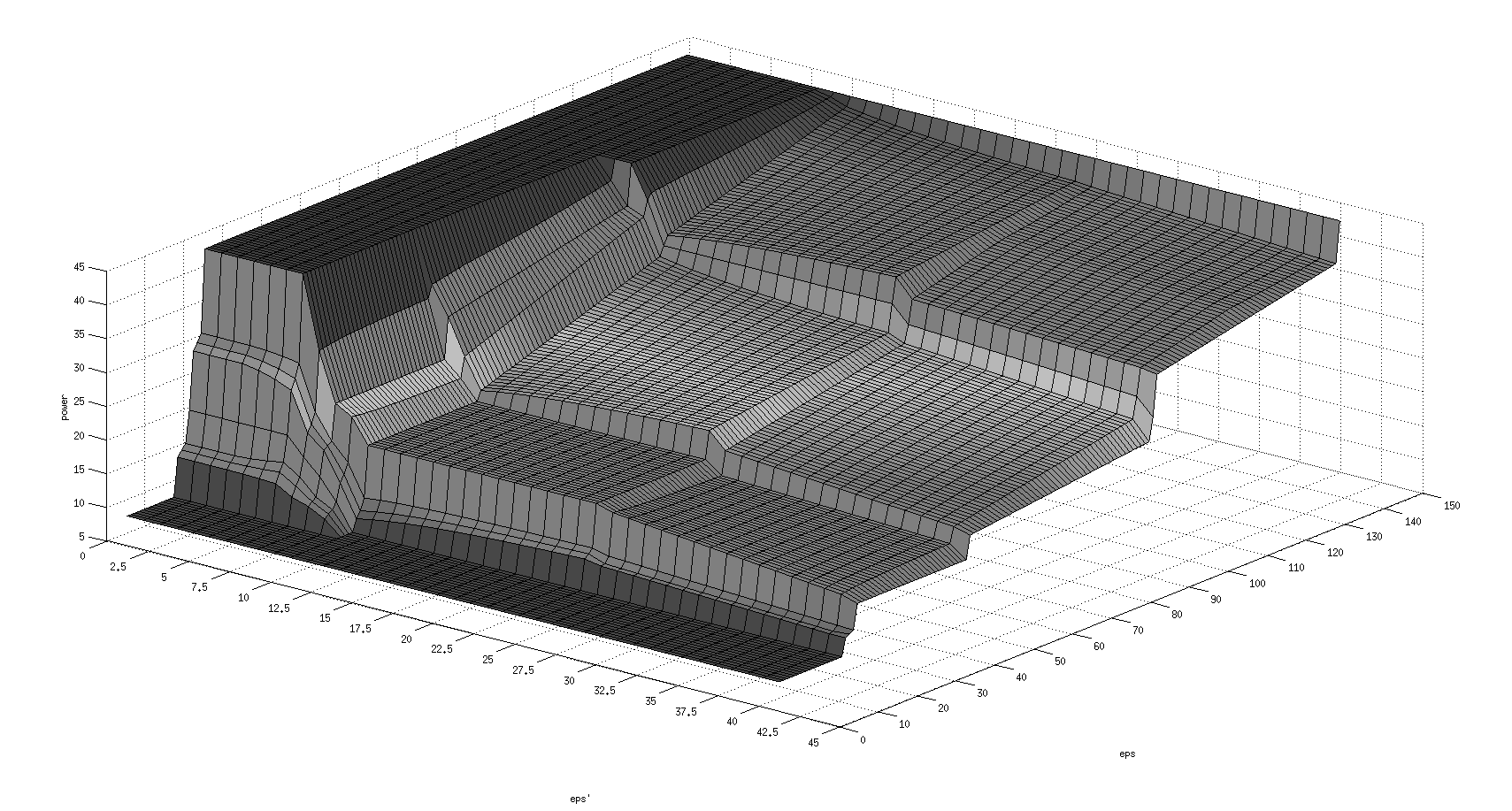Рисунок 17. Поверхность нечеткого ПД - регулятора в среде MATLAB

Наглядный график, по которому можно четко и точно проследить значения мощности системы.

Вывод: Проведенные испытания показали работоспособность алгоритма построенного для пелетной горелки и можно с уверенностью сказать, что этот алгоритм построенный на нечеткой логике является эффективным, для ее дальнейшей и продолжительной работы.

Список литературы:

1) Аверкин А. И., Батыршин И. 3., Блишун А. Ф., Силов В. Б., Тарасов В. Б. Нечеткие множества в моделях управления и искусственного интеллекта / Под ред. Д. А. Поспелова. — М.: Наука, 1986. — 312 с. — (Серия «Проблемы

искусственного интеллекта»)

2) Алиев Р. А., Церковный А.Э., Мамедова Г. А. Управление производством при нечеткой исходной информации / Ред.: В. Н. Вагин, В. И. Петухова. М.: Энергоатомиздат, 1991. —240 с.

3) Батыршин И.З., Недосекин А. О., Стецко А. А., Тарасов В. Б., Язенин

1. В., Ярушкина Н. Г. Нечеткие гибридные системы: Теория и практика / Под ред. Н. Г. Ярушкиной. — М.: Физматлит, 2007. — 208 с.

4) Заде Д. Понятие лингвистической переменной и его применение к приня­тию приближенных решений: Пер. с англ. Н.И.Ринго под ред. Н.Мо­исеева и С. А. Орловского — М.: Мир, 1976.- 165 с.— (Серия «Новое а зарубежной науке; Математика», вып.3 / Ред. серии А.Н.Колмогоров и С П. Ноликов)

5) Кофман Н. А. Введение в теорию нечетких множеств. С предисл. Л. А. Заде: Пер. с франц. В. В, Кузьмина под ред. С И, Травкина, С предисл. М. А. Ай-зврмана. — М.: Радио и связь, 1982. — 432 с.

6) Новак В., Перфильева И., Мочкорж И. Математические принципы нечеткой логики: Пер. с англ. под ред. А.Н.Аверкина. — М.: Физматлит. 2006,-352 с.