Типы функций принадлежности нечетких множеств
В практических приложениях теории нечетких множеств используется большое количество различных типов функций принадлежности. Здесь мы рассмотрим ряд как простых, так и сложных видов этих функций и обсудим их свойства.
• Функции принадлежности, состоящие из прямолинейных участков
Такие функции применяются на практике достаточно часто, что обусловлено их простотой. На рисунке 6 показаны различные формы наиболее часто используемой функции многоугольной формы.
Рисунок 6. Формы наиболее часто используемых кусочно-линейных функций принадлежности: а — крайняя левая функция принадлежности; б, ж — асимметричная треугольная функция принадлежности; в, з — асимметричная трапециевидная функция принадлежности; г —симметричная трапециевидная функция принадлежности; д — симметричная треугольная функция принадлежности; е — прямоугольная функция принадлежности; и — крайняя правая функция принадлежности
Существенным преимуществом многоугольных функций принадлежности является то, что для их определения требуется наименьший по сравнению с остальными функциями объем информации, который в данном случае ограничивается данными об угловых точках, что является весьма важным обстоятельством при моделировании систем в условиях ограниченности объема исходных данных. Чтобы определить многоугольную функцию принадлежности, на практике обычно требуется задать лишь модальное значение соответствующего нечеткого множества.
Достоинства многоугольных функций принадлежности
1.Для их задания требуется малый объем данных.
2.Простота модификации параметров (модальных значений) функции принадлежности на основе измеряемых значений входных и выходных величин системы.
3.Возможность получения в рамках модели отображения «вход—>выход» в виде гиперповерхности, состоящей из линейных участков.
4.Для многоугольных функций принадлежности легко обеспечивается выполнение условия разбиения единицы (в соответствии с которым сумма степеней принадлежности для любого элемента х должна равняться 1).
Недостатки многоугольных функций принадлежности
1. Многоугольные функции принадлежности не являются непрерывно дифференцируемыми
Структура, основные элементы и операции в нечетких моделях
На рисунке 7 представлена типовая структура нечеткой модели системы с двумя входами и одним выходом.
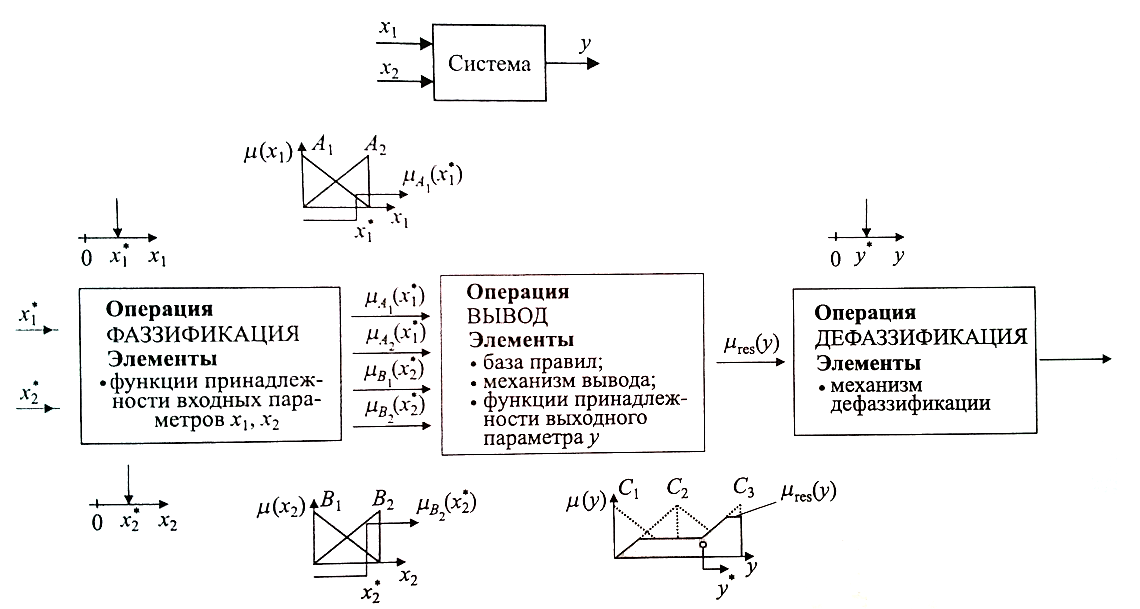
Рисунок 7. Структура нечеткой модели системы с двумя входами и одним выходом
На входы нечеткой модели поданы два четких числовых значения х1*, х2*. Блок «ФАЗЗИФИКАЦИЯ» (FUZZIFICATION) вычисляет их степени принадлежности входным нечетким множествам Аi Bj. Для выполнения указанной операции блок фаззификации должен иметь доступ к точно определенным функциям принадлежности µAi(X1), µBj(X2) входов. Примеры таких функций принадлежности приведены на рисунке 8.
Вычисленные и представленные на выходе блока фаззификации степени принадлежности µAi(X1*), µBj(X2*) дают информацию о том, в какой степени числовые значения х1*, х2* принадлежат конкретным нечетким множествам, т. е. насколько эти величины являются малыми (A1, В1) или большими (А2, В2).
Блок «ВЫВОД» (INFERENCE) на входе получает степени принадлежности µAi(X1*), µBj(X2*) и на выходе вычисляет так называемую результирующую функцию принадлежности выходного значения модели (рисунок 7). Данная функция обычно имеет сложную форму и определяется посредством вывода, который может быть осуществлен множеством способов. Для выполнения вычислений блок вывода должен включать в себя следующие строго определенные элементы:
• база правил,
• механизм вывода,
• функции принадлежности выходного параметра у. База правил содержит логические правила, которые задают имеющие место в системе причинно-следственные отношения между нечеткими значениями ее входных и выходных величин. База правил может например, иметь следующий вид:
R1: ЕСЛИ (Х1=А1) И (Х2=В1) ТО (у=С1),
R2: ЕСЛИ (Х1=А1) И (Х2=В2) ТО (у=С2),
R3: ЕСЛИ (Х1=А2) И (Х2=В1) ТО (у=С2),
R4: ЕСЛИ (Х1=А2) И (Х2=В2) ТО (у=С3),
где нечеткие значения входных параметров (А1 — малый, А2 — большой и т. д.) представлены на рисунке 8, а выходных — на рисунке 9
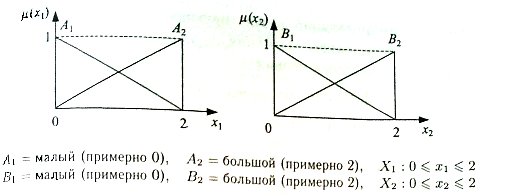
Рисунок 8. Примеры функций принадлежности нечетких множеств с указанием их области определения
Рисунок 9. Примеры функций принадлежности нечетких значений выхода модели с указанием области определения
Решение возложенной на блок вывода задачи, связанной с определением результирующей функции принадлежности µres(y) обеспечивается механизмом вывода, который состоит из следующих элементов:
IM1: элемент, вычисляющий степень выполнения каждого правила Ri в отдельности,
IМ2: элемент, вычисляющий активизированные функции принадлежности заключений каждого правила Ri
IM3: элемент, вычисляющий результирующую функцию принадлежности µres(y) выходного значения на основе активизированных заключений отдельных правил.
Приведем пример механизма вывода для системы с двумя входами:
IM1: агрегация условий правил с использованием оператора PROD для пересечения множеств (И) и оператора МАХ для объединения множеств (ИЛИ),
IM2: определение активизированных функций принадлежности заключений правил с использованием оператора импликации Мамдани,
IM3: определение результирующей функции принадлежности µres(y) выходного значения (аккумуляция) с использованием оператора МАХ.
Блок «ДЕФАЗЗИФИКАЦИИ» (DEFUZZIFICATION) на основе результирующей функции принадлежности µres(y) вычисляет четкое числовое значение у* выходного параметра, являющееся результатом для входных числовых значений х1*, х2*. Данная операция выполняется посредством механизма дефаззификации, который определяет метод вычисления. Примером механизма дефаззификации является метод центра тяжести.