2.18.Кількісне формулювання другого начала термодинаміки.

Для будь-якого оборотного не кругового процесу кількість теплоти не залежить від форми шляху:

2.19. Закон зростання ентропії. Процеси теплопередачі та розширення ідеального газу у вакуум.

δQ = 0

dS >= 0, S₁ – S₂ >= 0

В адіабатичній оболонці:

При необоротних процесах (розширення газу у вакуумі) ентропія зростає. При оборотних – не змінюється.

2.20.Закон зростання ентропії. Дифузія. Парадокс Гібсса.

П

ергородка А пропускає лише газ А, Б – Б.

ΔS_a = v_aRln(V/V_a)

ΔS_b = v_bRln(V/V_b)

Сумарна : ΔS = ΔS_a + ΔS_b = v_aRln(V/V_a) + + v_bRln(V/V_b) = /*V_a = V_b = V/2*/= (υ_a + υ_b)Rln2=/* Газ А прямує в газ Б, тому υ_a = υ_b = υ*/=2υRln2

А з іншого боку: ΔS = 0 ( макропараметри не змінюються Т,р,V = const ).

Виникає парадокс Гібсса: його розвязок полягає в тому, що властивості газів не можна наближати один до одного плавно.

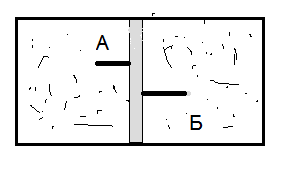
2.22. Межі застосування другого начала термодинаміки.

У явимо тут пристрій (“демона”), який пропускає в праву частину тільки швидкі, а в ліву — тільки повільні молекули. “Демон” спростовує 2 начало, яке забороняє самовільне виникнення різниці температур. Насправді парадоксу немає: друге начало термодинаміки застосовне тільки для макроскопічних тіл із великою кількістю частинок. Для “демона” газ не є макроскопічним тілом, якщо він виділяє окремі молекули.

2.23.Співвідношення між ентропією та імовірністю, формула Больцмана.

,де S-ентропія. S=S₁+S₂, p=p₁+p₂, -> f(p)=f(p₁)+f(p₂)->f(p₁p₂)=f(p₁)+f(p₂)

V2,S2

V1,S1

S=αln(p)+const

αln(p₁p₂)+const=αln(p₁)+const+αln(p₂)+const

const=01

V1

V ,

V2

V1

V2

, , , , ,

-формула Больцмана.

40