2.9 К.К.Д. Циклу Карно

К.к.д. теплової машини за означенням: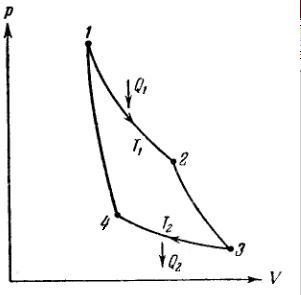

, де тепло, отримане від нагрівача, віддане холодильнику.

За першим началом термодинаміки:

.

Оскільки 2→3 і 4→1 є адіабатами, то виконуються наступні рівності:

;

.

( умова замкнутості циклу).

Підставимо все у початковий вираз:

Враховуючи умову замкненості, отримаємо:

2.10. Перша теорема Карно.

П

роцес без тертя оборотний у будь-якому розумінні.

А12 + А23 - А34 - А41 = А

N = A/Q = (Q1 - Q2 ) / Q1

К

оєфіцієнт корисної дії теплової машини, яка працює за оборотним циклом Карно, не залежить ні від робочої речовини, ні від конкретної теплової машини, а лише від температур нагрівача та холодильника.

1 - взяла Q1, виконала А, віддала Q2 .

2 - взяла Q1’, за рахунок виконання A’, віддала Q2’.

N = (Q1- Q2 ) / Q1

N’ = (Q1’ - Q2’)/ Q1’.

Доведемо, що N = N’.

Припустимо, що N’ > N. Підберемо цикл так щоб Q1 = Q1’. Одже отримаємо:

А - NQ1 > A’ - N Q1’.

A – A’ = (N - N’) Q > 0

Корисна робота виконана без використання холодильника -> невірно! Отже, N = N'

Припустимо, що N’ > N . Запускаємо машини в зворотньому напрямку, отримуємо суперечність, отже N = N’.

Звідси N = N!

2.11.Друга теорема Карно.

К КД теплової машини, що працює за необоротним циклом Карно не може перевищувати ККД машини, що працює за оборотним циклом К., між тими ж холодильником і нагрівачем.

N =A/Q = (Q1 - Q2 ) / Q1 = (Т1 - Т2) / Т1

Q1 = A1 = p1 (V2 - V1)

бA = pdV

p = RT/V

бА = RT1 (dV/V)

Cv dT + бA = 0

A23 = Cv(T2 - T1) = - Cv (T1 - T2) = -A41

TV^ɤ-1 = const, PV^ɤ = const

(V2/V1) = (V3/V4)

2.12. Третя теорема Карно.

ККД будь-якої машини (реальної) не може перевищувати ККД машини, що працює за оборотним циклом Карно, і цей цикл відбувається між найбільшою температурою нагрівача і найменшою температурою холодильника.

N = A / Q₁.

2.13. Методом циклів знайти залежність внутрішньої енергії ідеального газу від об`єму.

М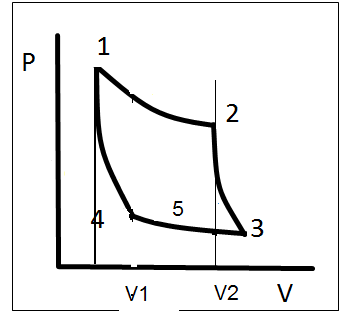 етод циклів.

f =(p, V, T) = 0

U (V, T) = 0

N = A / Q₁ = T₁ – T₂ / T₁, при малих р;

А = (V₂ – V₁)(δp / δT) (T₂ – T₁)

Q₁ = U₂ – U₁ – pΔV = (V₂ – V₁) + p(V₂V₁)

= T - p.

2.15. Нерівність Клаузіуса.

Якщо круговий процес не оборотний, то з нього випливає нерівність Клаузіуса . Внаслідок повернення в початкову точку через необоротний процес

Ентропія зростає!

2.16. Поняття про ентропію

Н езалежність суми від шляху, по якому проходить оборотний перехід, дає можливість стверджувати, що при оборотному процесі являє собою приріст деякої функції стану, яку назвемо ентропією(позначають S).

Для довільного процесу:

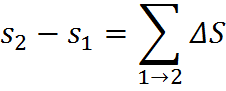
Для оборотного процесу приріст ентропії - відношення елементарної кількості теплоти, що отримує система, до температури, при якій це тепло отримане:

Ентропія ізольованої системи може збільшуватися(при протіканні необоротного процесу) або залишатися сталою(при протіканні оборотного процесу). Зменшуватися ентропія ізольованої системи не може. Для одного моля(якщо вважати теплоємність сталою):

2.17.Ентропійна діаграма. Її еквівалентність циклу Карно.

Цикл Карно. Ентропійна діаграма.

N = (Q₁ – Q₂ ) / Q₁ = [T₁(S₁ – S₂) – T₂(S₁ – S₂)] / T₁(S₁ – S₂) = (T₁ – T₂) / T₁ =

= 1 – T₂/T₁.

=>Q₁ = T₁ (S₁ – S₂), Q₂ = T₂ (S₁ – S₂)