14. Дослід Перрена. (за допомогою ф-ли Больцмана

Перрен використав ф-лу для перевірки барометричної ф-ли, визначення сталої Больцмана, або число Авогадро.

Е мульсія складається з двох незмішуваних рідин, одна з яких утворює маленькі краплі в іншій. Перрен приготував емульсії, в яких були частинки приблизно кулеподібної форми і приблизно однакового розміру. Фокусуючи мікроскоп на різних глибинах, Перрен спостерігав розподіл зважених частинок по висоті, рахуючи частинки, що потрапляли в поле зору мікроскопа. Ці досліди підтвердили формулу зміни концентрації , в якій також враховувалась втрата ваги у зв’язку з силою Архімеда. Перрен обчислив сталу Больцмана .

15. З об'єднаного розподілу молекул за швидкостями Максвела-Больцмана отримати розподіл Максвела

Розподіл Максвела-Больцмана для вірогідності знаходження молекули з потенційною енергією U в об’ємі dV з заданим імпульсом. Його також можна представити у вигляді двох ­множників.

Перший із них не що інше як розподіл Максвела. Для виокремлення цього множника з об‘єднаного закону достатньо проінтегрувати розподіл Максвела-Больцмана по об’єму.

- не залежить від об’єму

Скоротивши на отримаємо розподіл Максвела по імпульсам.

Аналогічно можна отримати розподіл Больцмана проінтегрувавши по імпульсу

16. З об'єднаного розподілу Максвелла-Больцмана отримати розподіл Больцмана.

17. З біноміального розподілу отримати розподіл Пуассона.

Умова: n>>m. m порядку 1..20

18.Дослід Перрена з броунівським рухом частинок по визначенню числа Авогадро

Ф ормула справедлива також для середнього значення квадрата багатьох послідовних переміщень однієї-єдиної частинки.

Перрен відмічав положення однієї конкретної частинки через положення Користувався він мікроскопом з нанесеною на окуляр координатною системою.Перрен вимірював зміщення Δх і знайшов середнє значення їх квадрата. Знаючи η, Т і радіус частинки α, він знайшов , де k знайшов з експеримента.

19. Обертальний броунівський рух

Бр. об. рух легко досліджується. На дуже тоненькій кварцовій нитці підвішується маленьке дзеркальце. Під дією ударів молекул оточуючого газу воно створює обертальні хаотичні коливання біля положення рівноваги. Це і є броунівський обертальний рух. Для його дослідження на дзеркальце пускають промінь світла, який після відбивання потрапляє на шкалу. По відхиленню на шкалі можна визначити кутове відхилення дзеркала. При гармонійних коливаннях середнє значення кінет. і потенц. енергій ½ kT, а енергія закрученої нитки ½ fφ², де φ – кут повороту дзеркала, f – модуль обертання нитки => f <φ²> = kT => .

20. Молекулярні пучки. Зміна кількості молекул у пучку внаслідок зіткнень молекул газу.

,де N-число молекул,dN-число «вибулих» молекул, dx-шлях, λ-довжина вільного пробігу. Проінтегруємо : , . Звідки або , dN- імовірність того, що частинка пройшла dx і не розсіялась.

2 1. Експериментальне визначення довжини вільного пробігу(досл. Борна – Бормана)

З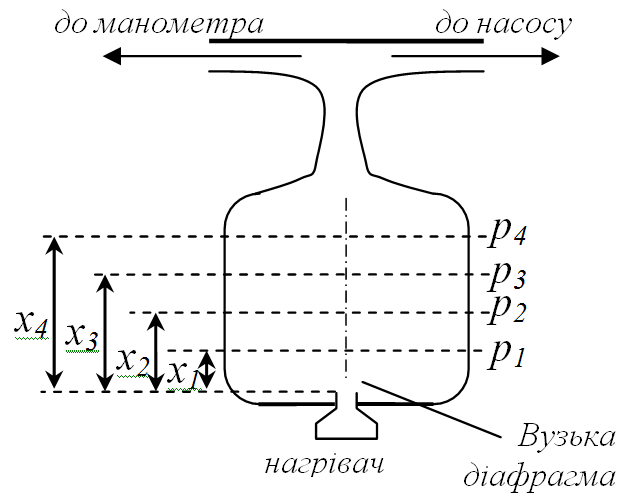 нагрівача потік випаровуваних атомів срібла проходить через вузьку діафрагму і виходить з неї вгору у вигляді чіткого окресленого атомного пучка. На шляху пучка розміщені 4 диски Р₁, Р₂, Р₃ і Р₄, відділені один від одного відстанями 1 см. В дисках вирізано круглі отвори, куди й прямує пучок атомів срібла, але до кожного з дисків прикріплено скляний квадрант. Квадранти повернуті на 90^о один відносно одного, так що разом повністю перекривають канал, утворений в дисках. При проходженні пучка на кожному квадранті осідає ¼ всіх атомів пучка. Різна віддаленість дисків до нагрівача спричинює різну густину осаду на кожному диску. Чим далі диск, тим менша густина. Описана система знаходиться в кварцовій трубі,де можна зробити той чи інший тиск повітря. Диски охолоджуються рідким азотом. Якщо розглянути густини осадів на б.-якій парі дисків, отримаємо(для першого й другого): , , де D₀ – густина осаду при мінімальному тиску. Тоді . Дослід показав, що значення λ відповідають наведеній теорії, також було показано, що λр залишається сталим при різних тисках.

22. В'язкість газів

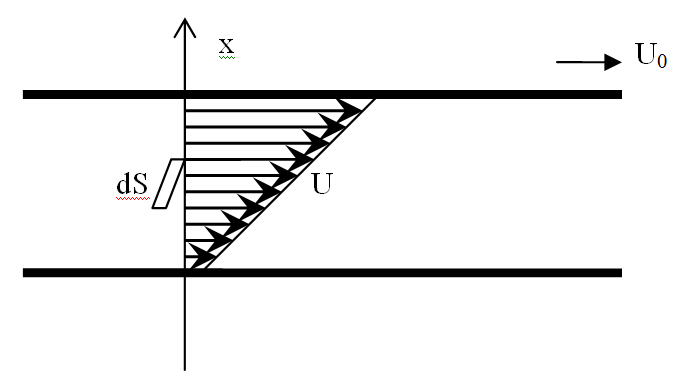
т еорія=практиці:

η(P): λ<<d->λ~1/n~1/P; ρ~n~P -> η не залежить від Р

λ>>d або λ~d->λне~1/P->η~P(вик.у в'язкісному маном.)

η(T): ->

23. дослід Шлейєрмахера

Н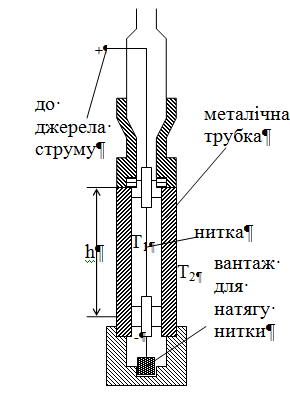 итку розжарюють до температури Т₁, а зовнішню оболонку утримють при температурі Т₂. Кількість теплоти, що протікає за одиницю часу через будь-який циліндричний переріз S (S=2πr): . Якщо h>>r, то Т вздовж осі циліндра стала. У стаціонарному стані W – потужність нагрівача. Тоді для коефіцієнта теплоємності א, знаючи h, r, вимірявши Т₁ і Т₂ отримуємо вираз:

24 Самодифузія . Коефіцієнт самодифузії , його залежність від тиску і температури

Самодифузія – дифузія газу самого в собі . Можна спостерігати при русі двох різних ізотопів одного і того ж газу . Коефіцієнт самодифузії :

Експеримент - Закон Фіка :

Теорія ( з теорії явищ переносу ) :

Залежності :

25.Термічна ефузія. Демонстрація Поля явища термічної ефузії.

П отік молекул через отвір називається ефузійним потоком, якщо довжина вільного пробігу набагато білбша за розмір отвору і довжини перегородки.

Вираз для термічної ефузії:

Красиву демонстрацію запропонував Р.Поль.

Т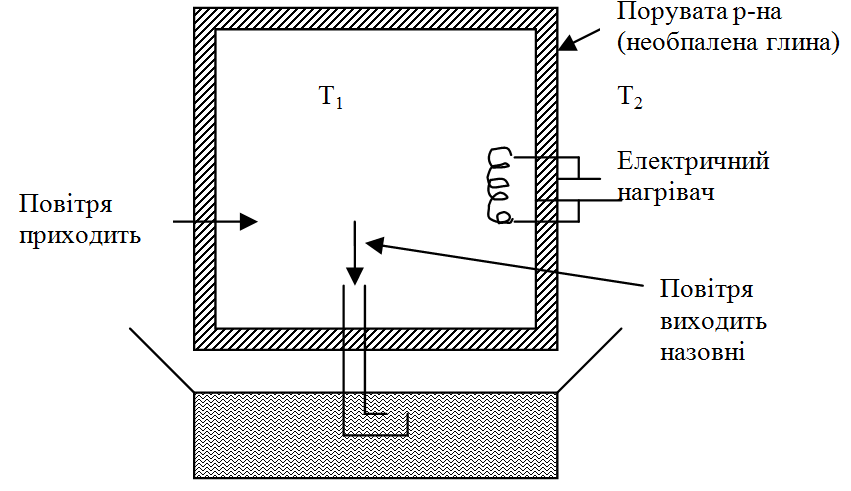 ₁>Т₂

Повітря ззовні безперервно всмоктується вередину. Тиск у посудині збільшується і надлишок повітря безперервно виходить назовні.

26. Ізотермічна ефузія. Демонстрація явища ізотермічної ефузії

П осудина розділена на дві частини пористою перегородкою. По різні сторони знаходяться різні гази, а розміри пор малі у порівнянні з довжиною вільного пробігу. P,T-const. Більш легкий газ швидше проходитиме через перегородку, ніж більш важкий. Кількість молекул щ пролітають крізь перегородку:

В початковий момент часу маємо:

Таким чином при рівності тем-ур і тисків маємо:

Д емонстрація явища

Стакан з пористої глини А поєднується гумовою трубкою з водним манометром М Зверху надітий непроникний стакан В. Через трубку D витікає водень. Внаслідок ефузії водень швидше повітря потрапляє в стакан А і витісняє його . Манометр показує підвищений тиск Якщо стакан В зняти, водень виходитиме зі стакана і манометр показуватиме понижений тиск.