§ 5. Функциональные ряды.

Ряд, членами которого являются функции, называется функциональным рядом:

.

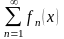Примеры.

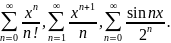
Если зафиксировать какое-то значение ,

,

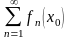то функциональный ряд становится обычным числовым рядом. Если ряд сходится, то ряд называется сходящимся в точке .

Примеры.

Исследуй на сходимость ряды

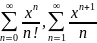
при

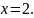
Множество всех значений , при которых ряд сходится, называется областью сходимости функционального ряда.

Пример.

Найти область сходимости ряда

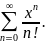
Ряд называется сходящимся равномерно к функции 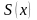на промежутке , если

.

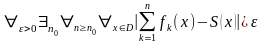Равномерная сходимость обозначается так:

 .

С равномерно сходящимися рядами приятно иметь дело, их можно дифференцировать и интегрировать:

; ,

но об этом чуть позже.

Обрати внимание, что если в определении равномерно сходящегося ряда поменять местами кванторы:

,

т.е. сначала зафиксировать точку , а только потом требовать всё остальное, то это уже не будет равномерная сходимость. Получится поточечная сходимость в произвольной точке .

Признак Вейерштрасса равномерной сходимости ряда.

Дан ряд , члены которого определены на . Если

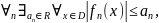
и при этом числовой ряд

сходится, то ряд сходится на равномерно.

Доказательство.

Из условия следует, что

.

По первой теореме сравнения (§ 2), из сходимости большего ряда следует сходимость меньшего, поэтому ряд тоже сходится. Но из абсолютной сходимости ряда следует, что он просто сходится, т.е. ряд сходится. Равномерно или поточечно? Так как в условии квантор стоит после 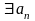, то сходимость будет равномерной, что и доказывает теорему.

Числовой ряд , обладающий свойством

,

называется мажорирующим.

Пример.

Найти область сходимости ряда

§ 6. Степенные ряды.

Ряд

называется степенным рядом. Это частный случай функционального ряда. В качестве 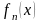выступает степенная функция , отсюда и название ряда.

Примеры

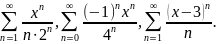
Теорема Абеля (о виде области сходимости степенного ряда).

Если числовой ряд 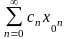сходится, то

.

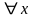
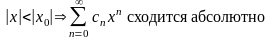Доказательство.

Если числовой ряд сходится, его общий член должен стремиться к нулю (§ 1):

,

поэтому последовательность является сходящейся. А всякая сходящаяся последовательность ограничена (глава I, § 5, св. 5), т.е.

.

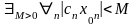Дальше всё просто:

.

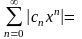
Ряд 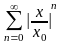является геометрическим со знаменателем , поэтому он сходится. Отсюда ряд тоже сходится, поэтому меньший ряд тем более сходится, а, значит, ряд сходится абсолютно, ч.т.д.

Из этой теоремы следует, что

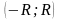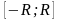1. область сходимости степенного ряда может быть только вида , или , или , т.е. это должен быть промежуток с центром в нуле. Число 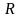называется радиусом сходимости степенного ряда.

2. Для нахождения радиуса сходимости степенного ряда можно рассматривать не сам ряд, а ряд из модулей.

Примеры.

Найти область сходимости рядов

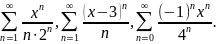
Теорема 2 (о равномерной сходимости степенного ряда)

Если - радиус сходимости степенного ряда , то он сходится равномерно на любом отрезке .