50. Capital Assets Pricing Model (capm).

Introduced by Sharpe, Lintner, and Mossin this model is often referred to as the Sharpe-Lintner-Mossin form of the Capital Asset Pricing Model (CAPM).

Being a measure of a security’s risk, Beta of a security is the central idea of this model. Since we assume that investors are concerned only with expected return and risk, the only dimensions of a security that need be of concern are expected return and Beta. Then we can graphically present a relationship between risk and return and the efficient frontier as follows:

T he security market line

The straight line in the Figure 5 is often referred to as the security market line (SML) and represents an efficient frontier. As the security market line is a straight line, then it can be mathematically described as a linear function that has the form:

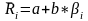(1)

As we see in Figure 5, the SML intersects the Y-axis at the point 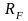. At the point of intercept Beta is equal to zero. Hence we have

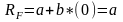
Now let us look at the point A, where Beta is equal to one. If we draw a straight line which would go through point A and is perpendicular to the X-axis, the intercept with the Y-axis would correspond the expected market return, or

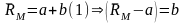
Putting these together and substituting into equation (1) yields

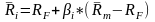
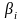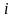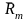where is the risk-free interest rate, is the Beta of security , and is expected return on the market. This relationship represents one of the most important discoveries in the field of finance. The main assumption behind the standard CAPM is that return on any security depends on variables that are not the functions of the asset being examined. Thus, the expected return on any asset can be related simply to this asset’s Beta, and the relationship between the expected return on any two assets can be related simply to their difference in Beta. The SML can be rewritten as follows:

(Expected return) = (Price of time) + (Amount of risk) * (Price of risk)

If a security lied above the SML, then all investors were buying it. In the result the price of this security would go up and its expected return would go down – the security would move downwards and lie exactly on the SML. If a security lied below the SML, then all investors were selling it. The price of this security would therefore go down and the expected return would go up – the security would move upwards and lie exactly on the SML line.

The CAPM gives a precise prediction of the relationship between the risk of an asset and its expected return.

To the market portfolio we add risk-free asset

The slope of the SML is equal to the Market Risk Premium and reflects investors' degree of risk aversion at a given time. When used in portfolio management, a single asset is plotted against the SML using its own beta and historical rate of return. If the plot of the asset falls above the SML it is considered to have a good rate of return relative to its risk, and vice versa if it falls below.

Required rate of return for particular share equals risk free rate of return + beta coefficient multiplied by the difference between market rate of return and risk free rate of return

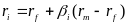
We can calculate the required rate of return knowing the risk rate. Beta is the measure of systematic risk (risk of the market). It describes how the expected return of a stock or portfolio depends on the return of the financial market as a whole.

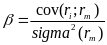
An asset with a beta of 0 means that its price is not at all correlated with the market; that asset is independent. A positive beta means that the asset generally follows the market. A negative beta shows that the asset inversely follows the market; the asset generally decreases in value if the market goes up. In case when beta = 1, the risk of an asset is similar with the risk of the market portfolio.

Nonsystematic risk is a risk of particular company. Systematical risks – politics, legislation, inflation, economic cycles.

By increasing the number of shares in the portfolio its riskiness can be reduced due to reduction of the non-systematic risk:

Sigma

N – number of various shares in the portfolio

51. Approaches to measuring market risk. Long-term investments planning.

Market risk - the possibility that future earnings could be adversely affected by a change in market prices caused by movements in interest rates or exchange rates.

Market risk is exposure to the uncertain market value of a portfolio. Market risk is managed with a short-term focus. Long-term losses are avoided by avoiding losses from one day to the next. On a tactical level, traders and portfolio managers employ a variety of risk metrics —duration and convexity, beta, etc. – to assess their exposures. On a more strategic level, organizations manage market risk by applying risk limits to traders' or portfolio managers' activities. Increasingly, value-at-risk is being used to define and monitor these limits. Some organizations also apply stress testing to their portfolios.

Risk measures tend to be categorized according to the risk metrics they support. There are measures of duration, measures of delta, etc.

Duration and convexity are factor sensitivities that describe exposure to parallel shifts in the spot curve. They can be applied to individual fixed income instruments or to entire fixed income portfolios.

The idea behind duration is simple. Suppose a portfolio has a duration of 3 years. Then that portfolio's value will decline about 3% for each 1% increase in interest rates—or rise about 3% for each 1% decrease in interest rates. Now let's consider convexity. If duration summarized the most significant piece of information about a bond or a portfolio's sensitivity to interest rates, convexity summarizes the second-most significant piece of information. Duration captured the fact that spot curve was downward sloping. It did not, however, capture its upward curvature. Convexity describes curvature.

Value at risk is a single, summary, statistical measure of possible portfolio losses. Specifically, value at risk is a measure of losses due to "normal" market movements. Losses greater than the value at risk are suffered only with a specified small probability. Subject to the simplifying assumptions used in its calculation, value at risk aggregates all of the risks in a portfolio into a single number suitable for use in the boardroom, reporting to regulators, or disclosure in an annual report. Once one crosses the hurdle of using a statistical measure, the concept of value at risk is straightforward to understand. It is simply a way to describe the magnitude of the likely losses on the portfolio.

Any portfolio manager must understand what the weak spot is in his portfolio. Naturally, this is the first set of scenarios to simulate. By determining the change in value of his portfolio under stressful conditions (called "stress-testing"), the portfolio manager has a better perception of where the risks in his portfolio lie. At that point, he can make trades that reduce this risk to levels with which he is comfortable. Without this kind of stress-testing, he will be forced to react in a moving market, a situation that can exacerbate his market losses. In a complex derivatives portfolio, stress-testing that reveals excessively risky exposures either to movements in the underlying cash rate or shifts in implied volatility or interest rates (or combinations of these factors) is said to identify "risk holes."

Risk limits (or simply limits) are a device for authorizing specific forms of risk taking.

Long-term investment planning

Capital Budgeting is the process by which the firm decides which long-term investments to make. Capital Budgeting projects, i.e., potential long-term investments, are expected to generate cash flows over several years. The decision to accept or reject a Capital Budgeting project depends on an analysis of the cash flows generated by the project and its cost. The following three Capital Budgeting decision rules will be presented:

• Payback Period (When exactly do we get our money back, when does our project break even)

• Net Present Value (NPV)

• Internal Rate of Return (IRR) - IRR is the percentage amount of profit you get by investing in a certain project.

A Capital Budgeting decision rule should satisfy the following criteria:

• Must consider all of the project's cash flows.

• Must consider the Time Value of Money (The Time Value of Money concepts will be grouped into two areas: Future Value and Present Value. Future Value describes the process of finding what an investment today will grow to in the future. Present Value describes the process of determining what a cash flow to be received in the future is worth in today's dollars.)

• Must always lead to the correct decision when choosing among Mutually Exclusive Projects.

Beta Coefficient

Beta measures a stock's volatility, the degree to which a stock price fluctuates in relation to the overall market. Investment analysts use the Greek letter beta, ß. It is calculated using regression analysis. A beta of 1 indicates that the security's price will move with the market. A beta greater than 1 indicates that the security's price will be more volatile than the market, and a beta less than 1 means that it will be less volatile than the market.

Many utility stocks have a beta of less than 1. Conversely most high-tech Nasdaq-based stocks have a beta greater than one; they offer a higher rate of return, but they are also very risky. Let's give an illustration by using a hypothetical company, "Bob's Beer Company," which has a beta of 2. This means it is two times as volatile as the overall market. Let's say we expect the market to provide a return of 10% on an investment. We would expect Bob's Beer Company to return 20%. On the other hand, if the market were to decline and provide a return of -6%, investors in Bob's Beer Company could expect a loss of 12%. Beta expresses the fundamental tradeoff between minimizing risk and maximizing return.

Here is a basic guide to various betas:

• Negative beta - A beta less than 0 is possible but highly unlikely. People used to think that gold and gold stocks should have negative betas because they tended to do better when the stock market declined, but this hasn't been true overall.

• Beta = 0 - Basically this is cash (assuming no inflation).

• Beta between 0 and 1 - Low-volatility investments, such as utilities, are usually in this range

• Beta = 1 - This is the same as an index, such as the S&P 500 or some other index fund.

• Beta greater than 1 - This denotes anything more volatile than the broad-based index, like a sector fund.

• Beta greater than 100 - This is impossible because the stock would be expected go to zero on any decline in the stock market. The beta never gets higher than two to three.