2.4. Алгоритмы шифрования
На данный момент существует множество методов шифрования, от очень простых и древних, как например «Шифр Цезаря», до более сложных и новых, таких как «Шифр ЭльГамаля».
Шифр Цезаря, также известный как шифр сдвига, код Цезаря или сдвиг Цезаря - один из самых простых и наиболее широко известных методов шифрования [3].
Шифр Цезаря - это вид шифра подстановки, в котором каждый символ в открытом тексте заменяется буквой находящейся на некоторое постоянное число позиций правее него в алфавите. Например, в шифре со сдвигом 3, «А» была бы заменена на «Г», «Б» станет «Д», и так далее. Более наглядно шифр Цезаря отображен на рисунке:
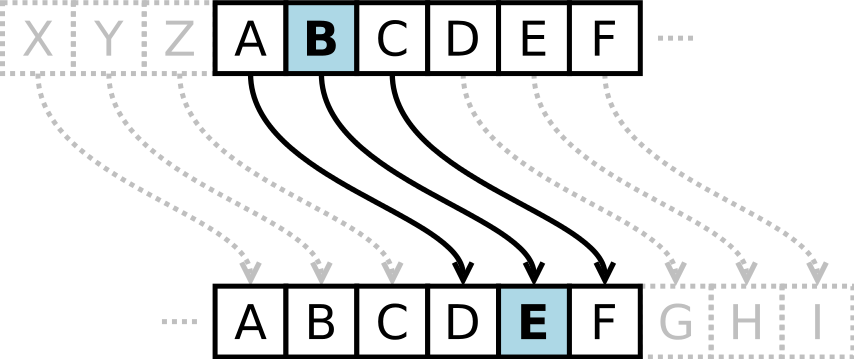
Рис. 2.2. Шифр Цезаря
Шифр назван в честь римского императора Гая Юлия Цезаря, использовавшего его для секретной переписки со своими генералами.
Если сопоставить каждому символу алфавита его порядковый номер (нумеруя с 0), то шифрование и дешифрование можно выразить формулами модульной арифметики:
y = (x+k) mod n (2.1)
x = (y-k) mod n (2.2)
где, x – символ открытого текста, у – символ шифрованного текста, n – мощность алфавита, а k – ключ.
Существует большое количество простых методов шифрования не достаточных для хорошей защиты информации, поэтому криптографы постоянно вели поиски более эффективных систем открытого шифрования, и в 1985 году ЭльГамаль предложил следующую схему на основе возведения в степень по модулю большого простого числа [1]. Для этого задается большое простое число Р. Сообщения представляются целыми числами S из интервала (1,Р). Оригинальный протокол передачи сообщения выглядит в варианте Шамира, одного из авторов RSA, так:
Отправитель А и получатель B знают лишь P. А генерирует случайное число Х из интервала (1,Р) и В тоже генерирует случайное числоY из того же интервала.
А шифрует сообщение по формуле (2.3) и отправляет его В.
S1 = Sx MOD P (2.3)
В шифрует его своим ключом по формуле (2.4) и посылает S2 к А.
S2 = S1Y MOD P (2.4)
A «снимает» свой ключ по формуле (2.5) и возвращает S3 к В.
S3=S2-X MOD P (2.5)
Получатель В расшифровывает сообщение по формуле:
S=S3-Y MOD P (2.6)
В системе ЭльГамаля большая степень защиты, чем у алгоритма RSA достигается с тем же по размеру N, что позволяет почти на порядок увеличить скорость шифрования и расшифрования. Криптостойкость системы ЭльГамаля основана на том, что можно легко вычислить степень целого числа, то есть произвести умножение его самого на себя любое число раз так же, как и при операциях с обычными числами. Однако трудно найти показатель степени, в которую нужно возвести заданное число, чтобы получить другое тоже заданное. В общем случае эта задача дискретного логарифмирования кажется более трудной, чем разложение больших чисел на простые сомножители, на основании чего можно предполагать, что сложности вскрытия систем RSA и ЭльГамаля будут сходными. С точки зрения практической реализации, как программным, так и аппаратным способом ощутимой разницы между этими двумя стандартами нет. Однако в криптостойкости они заметно различаются. Если рассматривать задачу разложения произвольного целого числа длиной в 512 бит на простые сомножители и задачу логарифмирования целых чисел по 512 бит, вторая задача, по оценкам математиков, несравненно сложнее первой. Однако есть еще одна особенность. Если в системе, построенной с помощью алгоритма RSA, криптоаналитику удалось разложить открытый ключ N одного из абонентов на два простых числа, то возможность злоупотреблений ограничивается только этим конкретным пользователем. В случае же системы, построенной с помощью алгоритма ЭльГамаля, угрозе раскрытия подвергнуты все абоненты криптографической сети.