2. Построение прямой, проходящей через данную точку, перпендикулярной данной.

1. О кружность с центром в данной точке.

2. Отметить точки пересечения с данной прямой.

3. Построить одинаковые пересекающиеся окружности с центрами в этих точках.

4. Прямая через эти точки пересечения.

G DHE – ромб, диагонали взаимно перпендикулярны. Прямая проходит через точку, так как серпер – ГМТ равноудалённых от двух точек.

Билет №14

1. Теорема Менелая (прямая и обратная)

Теорема Менелая (ок. 100 г. н.э.). Пусть прямая пересекает треугольник ABC, причём C₁ – точка пересечения со стороной AB, A₁ – со стороной BC, B₁ – с продолжением стороны AC.

Тогда выполняется равенство:

Д оказательство. Проведём через точку C прямую CK параллельно AB (K – точка пересечения с C₁B₁)

Теорема доказана.

Обратная теорема Менелая. Пусть дан треугольник ABC и точки A₁, B₁, C₁ на прямых BC, AC, BA, причём

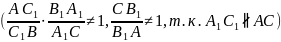
Тогда точки A₁, B₁ и C₁ лежат на одной прямой.

Д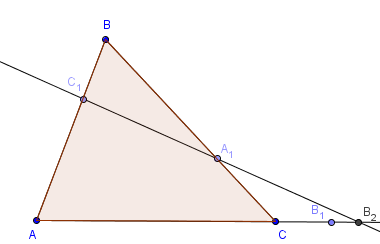 оказательство. Проведём A₁C₁. Отметим точку пересечения с прямой AC как B₂.

Из аксиомы об откладывании отрезка следует, что B₁ совпадает с B₂.

Теорема доказана.

Билет №23

1. Окружность Аполлония.

О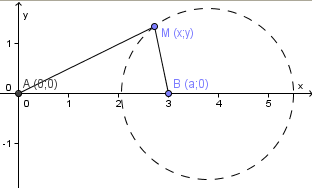 пределение 1. Окружность Аполлония – это ГМТ плоскости, соотношение расстояний от которых до двух заданных точек – величина постоянная.

О пределение 2. Окружность Аполлония – это ГМТ плоскости, сумма квадратов расстояний от которых до двух заданных точек постоянна (фиксирована).

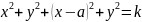
Билет №24

1. Теорема Чевы (прямая и обратная).

Теорема Чевы (1678 г.). Пусть точки A₁, B₁, C₁ лежат соответственно на сторонах BC, AC, AB. Пусть отрезки AA₁, BB₁ и CC₁ (чевианы) пересекаются в одной точке. Тогда:

Доказательство. Пусть O – точка пересечения AA₁, BB₁ и CC₁. Опустим из вершин A и C перпендикуляры на прямую BB₁. L и K – основания перпендикуляров.

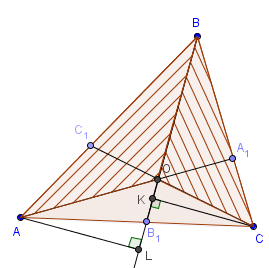
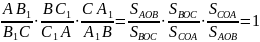
Теорема доказана.

Обратная теорема Чевы. Пусть дан треугольник ABC и точки A, B, C лежат соответственно на сторонах BC, CA, AB. Пусть выполняется соотношение:

Тогда отрезки AA₁, BB₁, CC₁ пересекаются в одной точке.

Д оказательство. Пусть O – точка пересечения AA₁ и BB₁ и прямая CO пересекает сторону AB в точке C₂. Теперь достаточно доказать, что C₁ совпадает с C₂.

Из аксиомы об откладывании отрезка следует, что C₁ совпадает с C₂.

Теорема доказана.